Absolute difference

Short description: Absolute value of (x - y), a metric

Showing the absolute difference of real numbers $x$ and $y$ as the distance between them on the real line.

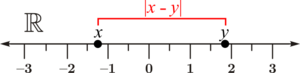
The absolute difference of two real numbers $x$ and $y$ is given by $|x-y|$, the absolute value of their difference. It describes the distance on the real line between the points corresponding to $x$ and $y$, and is a special case of the L^p distance for all $1\le p\le \mathrm{\infty }$. Its applications in statistics include the absolute deviation from a central tendency.

Properties

Absolute difference has the following properties:

• For $x\ge 0$, $|x-0|=x$ (zero is the identity element on non-negative numbers)
• For all $x$, $|x-x|=0$ (every element is its own inverse element)
• $|x-y|\ge 0$ (non-negativity)
• $|x-y|=0$ if and only if $x=y$ (nonzero for distinct arguments).
• $|x-y|=|y-x|$ (symmetry or commutativity).
• $|x-z|\le |x-y|+|y-z|$ (the triangle inequality); equality holds if and only if $x\le y\le z$ or $x\ge y\ge z$.

Because it is non-negative, nonzero for distinct arguments, symmetric, and obeys the triangle inequality, the real numbers form a metric space with the absolute difference as its distance, the familiar measure of distance along a line. It has been called "the most natural metric space", and "the most important concrete metric space". This distance generalizes in many different ways to higher dimensions, as a special case of the L^p distances for all $1\le p\le \mathrm{\infty }$, including the $p=1$ and $p=2$ cases (taxicab geometry and Euclidean distance, respectively). It is also the one-dimensional special case of hyperbolic distance.

Instead of $|x-y|$, the absolute difference may also be expressed as $$\max (x,y)-\min (x,y).$$ Generalizing this to more than two values, in any subset $S$ of the real numbers which has an infimum and a supremum, the absolute difference between any two numbers in $S$ is less or equal then the absolute difference of the infimum and supremum of $S$.

The absolute difference takes non-negative integers to non-negative integers. As a binary operation that is commutative but not associative, with an identity element on the non-negative numbers, the absolute difference gives the non-negative numbers (whether real or integer) the algebraic structure of a commutative magma with identity.

Applications

The absolute difference is used to define the relative difference, the absolute difference between a given value and a reference value divided by the reference value itself.

In the theory of graceful labelings in graph theory, vertices are labeled by natural numbers and edges are labeled by the absolute difference of the numbers at their two vertices. A labeling of this type is graceful when the edge labels are distinct and consecutive from 1 to the number of edges.

As well as being a special case of the L^p distances, absolute difference can be used to define Chebyshev distance (L^∞), in which the distance between points is the maximum or supremum of the absolute differences of their coordinates.

In statistics, the absolute deviation of a sampled number from a central tendency is its absolute difference from the center, the average absolute deviation is the average of the absolute deviations of a collection of samples, and least absolute deviations is a method for robust statistics based on minimizing the average absolute deviation.

External links

• Weisstein, Eric W.. "Absolute Difference". http://mathworld.wolfram.com/AbsoluteDifference.html.