Graham scan

Graham's scan is a method of finding the convex hull of a finite set of points in the plane with time complexity O(n log n). It is named after Ronald Graham, who published the original algorithm in 1972.[1] The algorithm finds all vertices of the convex hull ordered along its boundary. It uses a stack to detect and remove concavities in the boundary efficiently.
Algorithm
This section does not cite any external source. HandWiki requires at least one external source. See citing external sources. (February 2024) (Learn how and when to remove this template message) |
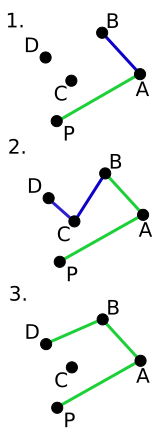
The first step in this algorithm is to find the point with the lowest y-coordinate. If the lowest y-coordinate exists in more than one point in the set, the point with the lowest x-coordinate out of the candidates should be chosen. Call this point P. This step takes O(n), where n is the number of points in question.
Next, the set of points must be sorted in increasing order of the angle they and the point P make with the x-axis. Any general-purpose sorting algorithm is appropriate for this, for example heapsort (which is O(n log n)).
Sorting in order of angle does not require computing the angle. It is possible to use any function of the angle which is monotonic in the interval . The cosine is easily computed using the dot product, or the slope of the line may be used. If numeric precision is at stake, the comparison function used by the sorting algorithm can use the sign of the cross product to determine relative angles.
If several points are of the same angle, either break ties by increasing distance (Manhattan or Chebyshev distance may be used instead of Euclidean for easier computation, since the points lie on the same ray), or delete all but the furthest point.
The algorithm proceeds by considering each of the points in the sorted array in sequence. For each point, it is first determined whether traveling from the two points immediately preceding this point constitutes making a left turn or a right turn. If a right turn, the second-to-last point is not part of the convex hull, and lies 'inside' it. The same determination is then made for the set of the latest point and the two points that immediately precede the point found to have been inside the hull, and is repeated until a "left turn" set is encountered, at which point the algorithm moves on to the next point in the set of points in the sorted array minus any points that were found to be inside the hull; there is no need to consider these points again. (If at any stage the three points are collinear, one may opt either to discard or to report it, since in some applications it is required to find all points on the boundary of the convex hull.)
Again, determining whether three points constitute a "left turn" or a "right turn" does not require computing the actual angle between the two line segments, and can actually be achieved with simple arithmetic only. For three points , and , compute the z-coordinate of the cross product of the two vectors and , which is given by the expression . If the result is 0, the points are collinear; if it is positive, the three points constitute a "left turn" or counter-clockwise orientation, otherwise a "right turn" or clockwise orientation (for counter-clockwise numbered points).
This process will eventually return to the point at which it started, at which point the algorithm is completed and the stack now contains the points on the convex hull in counterclockwise order.
Time complexity
This section does not cite any external source. HandWiki requires at least one external source. See citing external sources. (February 2024) (Learn how and when to remove this template message) |
Sorting the points has time complexity O(n log n). While it may seem that the time complexity of the loop is O(n2), because for each point it goes back to check if any of the previous points make a "right turn", it is actually O(n), because each point is considered at most twice in some sense. Each point can appear only once as a point in a "left turn" (because the algorithm advances to the next point after that), and as a point in a "right turn" (because the point is removed). The overall time complexity is therefore O(n log n), since the time to sort dominates the time to actually compute the convex hull.
Pseudocode
The pseudocode below uses a function ccw: ccw > 0 if three points make a counter-clockwise turn, ccw < 0 if clockwise, and ccw = 0 if collinear. (In real applications, if the coordinates are arbitrary real numbers, the function requires exact comparison of floating-point numbers, and one has to beware of numeric singularities for "nearly" collinear points.)
Then let the result be stored in the stack.
let points be the list of points
let stack = empty_stack()
find the lowest y-coordinate and leftmost point, called P0
sort points by polar angle with P0, if several points have the same polar angle then only keep the farthest
for point in points:
# pop the last point from the stack if we turn clockwise to reach this point
while count stack > 1 and ccw(next_to_top(stack), top(stack), point) <= 0:
pop stack
push point to stack
end
Now the stack contains the convex hull, where the points are oriented counter-clockwise and P0 is the first point.
Here, next_to_top() is a function for returning the item one entry below the top of stack, without changing the stack, and similarly, top() for returning the topmost element.
This pseudocode is adapted from Introduction to Algorithms.
Notes
The same basic idea works also if the input is sorted on x-coordinate instead of angle, and the hull is computed in two steps producing the upper and the lower parts of the hull respectively. This modification was devised by A. M. Andrew.[2] It has the same basic properties as Graham's scan.[3]
Graham's original description involved sorting around an interior point of the convex hull, rather than one of its vertices.[1] For the same choice of a pivot point for the sorting algorithm, connecting all of the other points in their sorted order around this point rather than performing the remaining steps of the Graham scan produces a star-shaped polygon, a polygonalization of the input.[4]
The stack technique used in Graham's scan is very similar to that for the all nearest smaller values problem, and parallel algorithms for all nearest smaller values may also be used (like Graham's scan) to compute convex hulls of sorted sequences of points efficiently.[5]
Numerical robustness
Numerical robustness is an issue to deal with in algorithms that use finite-precision floating-point computer arithmetic. A 2004 paper analyzed a simple incremental strategy, which can be used, in particular, for an implementation of the Graham scan.[6] The stated goal of the paper was not to specifically analyze the algorithm, but rather to provide a textbook example of what and how may fail due to floating-point computations in computational geometry.[6] Later D. Jiang and N. F. Stewart[7] elaborated on this and using the backward error analysis made two primary conclusions. The first is that the convex hull is a well-conditioned problem, and therefore one may expect algorithms which produce an answer within a reasonable error margin. Second, they demonstrate that a modification of Graham scan which they call Graham-Fortune (incorporating ideas of Steven Fortune for numeric stability[8]) does overcome the problems of finite precision and inexact data "to whatever extent it is possible to do so".
See also
References
- ↑ 1.0 1.1 Graham, R.L. (1972). "An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set". Information Processing Letters 1 (4): 132–133. doi:10.1016/0020-0190(72)90045-2. http://www.math.ucsd.edu/~ronspubs/72_10_convex_hull.pdf.
- ↑ Andrew, A. M. (1979). "Another efficient algorithm for convex hulls in two dimensions". Information Processing Letters 9 (5): 216–219. doi:10.1016/0020-0190(79)90072-3.
- ↑ De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars, Mark (2008). Computational Geometry Algorithms and Applications. Berlin: Springer. pp. 2–14. doi:10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5. https://archive.org/details/computationalgeo00berg_122.
- ↑ Arkin, Esther M.; Fekete, Sándor P.; Hurtado, Ferran; Mitchell, Joseph S. B.; Noy, Marc; Sacristán, Vera; Sethia, Saurabh (2003). "Discrete and Computational Geometry: The Goodman-Pollack Festschrift". in Aronov, Boris; Basu, Saugata; Pach, János et al.. 25. Berlin: Springer. pp. 139–156. doi:10.1007/978-3-642-55566-4_6. ISBN 978-3-642-62442-1.
- ↑ Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993). "Optimal double logarithmic parallel algorithms based on finding all nearest smaller values". Journal of Algorithms 14 (3): 344–370. doi:10.1006/jagm.1993.1018..
- ↑ 6.0 6.1 Kettner, Lutz; Mehlhorn, Kurt; Pion, Sylvain; Schirra, Stefan; Yap, Chee (2008). "Classroom examples of robustness problems in geometric computations". Computational Geometry 40 (1): 61–78. doi:10.1016/j.comgeo.2007.06.003. http://hal.inria.fr/docs/00/34/43/10/PDF/RevisedClassroomExamples.pdf. (An earlier version was reported in 2004 at ESA'2004)
- ↑ D. Jiang and N. F. Stewart, Backward error analysis in computational geometry , Computational Science and Its Applications - ICCSA 2006 Volume 3980 of the series Lecture Notes in Computer Science, pp 50–59
- ↑ Fortune, Steven (1989). "Stable maintenance of point set triangulations in two dimensions". 30th Annual Symposium on Foundations of Computer Science. 30. pp. 494–499. doi:10.1109/SFCS.1989.63524. ISBN 0-8186-1982-1. http://www.computer.org/csdl/proceedings/focs/1989/1982/00/063524.pdf.
Further reading
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "33.3: Finding the convex hull". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 949–955. ISBN 0-262-03293-7.
 |
