Half-logistic distribution

Short description: Concept in statistics

Half-logistic distribution

Probability density function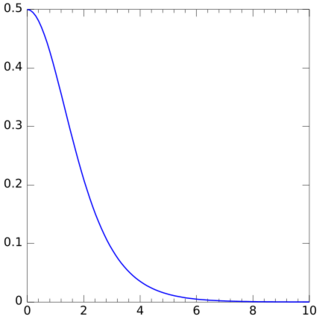
Cumulative distribution function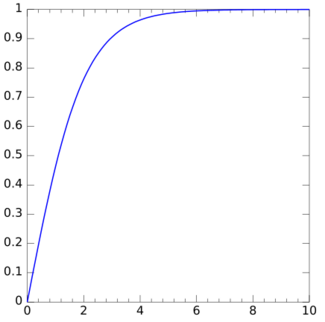
Support	$k\in [0;\mathrm{\infty })$
PDF	$\frac{2e^{-k}}{(1+e^{-k}{)}^2}$
CDF	$\frac{1-e^{-k}}{1+e^{-k}}$
Mean	$\ln (4)=1.386\dots$
Median	$\ln (3)=1.0986\dots$
Mode	0
Variance	${\pi }^2/3-(\ln (4){)}^2=1.368\dots$
Entropy	$\log \left(\frac{e^2}{2}\right)$

In probability theory and statistics, the half-logistic distribution is a continuous probability distribution—the distribution of the absolute value of a random variable following the logistic distribution. That is, for

$X=|Y|$

where Y is a logistic random variable, X is a half-logistic random variable.

Specification

Cumulative distribution function

The cumulative distribution function (cdf) of the half-logistic distribution is intimately related to the cdf of the logistic distribution. Formally, if F(k) is the cdf for the logistic distribution, then G(k) = 2F(k) − 1 is the cdf of a half-logistic distribution. Specifically,

$G(k)=\frac{1-e^{-k}}{1+e^{-k}}\text{ for }k\ge 0.$

Probability density function

Similarly, the probability density function (pdf) of the half-logistic distribution is g(k) = 2f(k) if f(k) is the pdf of the logistic distribution. Explicitly,

$g(k)=\frac{2e^{-k}}{(1+e^{-k}{)}^2}\text{ for }k\ge 0.$

References

• Johnson, N. L.; Kotz, S.; Balakrishnan, N. (1994). "23.11". Continuous univariate distributions. 2 (2nd ed.). New York: Wiley. p. 150. 
• George, Olusegun; Meenakshi Devidas (1992). "Some Related Distributions". in N. Balakrishnan. Handbook of the Logistic Distribution. New York: Marcel Dekker, Inc.. pp. 232–234. ISBN 0-8247-8587-8. 
• Olapade, A.K. (2003), "On characterizations of the half-logistic distribution", InterStat 2003 (February): 2, ISSN 1941-689X, http://interstat.statjournals.net/YEAR/2003/articles/0302002.pdf