Hexagonal pyramid
| Hexagonal pyramid | |
|---|---|
 | |
| Type | Pyramid |
| Faces | 6 triangles 1 hexagon |
| Edges | 12 |
| Vertices | 7 |
| Symmetry group | |
| Dual polyhedron | self-dual |
| Properties | convex |
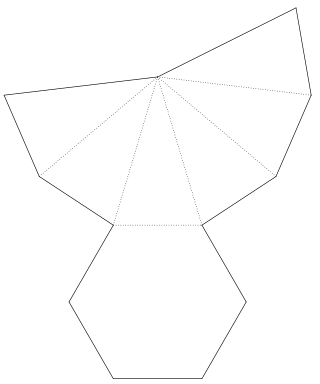
| Net | |
 | |
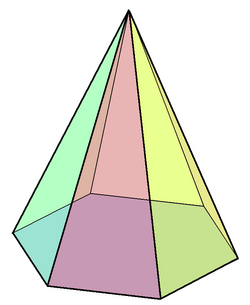
File:Hexagonal pyramid.stl In geometry, a hexagonal pyramid is a pyramid with a hexagonal base upon which are erected six triangular faces that meet at a point (the apex). Like any pyramid, it is self-dual.
Properties
A hexagonal pyramid has seven vertices, twelve edges, and seven faces. One of its faces is hexagon, a base of the pyramid; six others are triangles. Six of the edges make up the hexagon by connecting its six vertices, and the other six edges are known as the lateral edges of the pyramid, meeting at the seventh vertex called the apex.
Like other right pyramids with a regular polygon as a base, this pyramid has pyramidal symmetry of cyclic group : the pyramid is left invariant by rotations of one, two, three, four, and five in six of a full turn around its axis of symmetry, the line connecting the apex to the center of the base. It is also mirror symmetric relative to any perpendicular plane passing through a bisector of the base.[1] It can be represented as the wheel graph ; more generally, a wheel graph is the representation of the skeleton of a -sided pyramid.[2] It is self-dual, meaning its dual polyhedron is the hexagonal pyramid itself.[3]
References
- ↑ Alexander, Daniel C.; Koeberlin, Geralyn M. (2014). Elementary Geometry for College Students (6th ed.). Cengage Learning. p. 403. ISBN 978-1-285-19569-8. https://books.google.com/books?id=EN_KAgAAQBAJ&pg=PA403.
- ↑ Pisanski, Tomaž; Servatius, Brigitte (2013). Configuration from a Graphical Viewpoint. Springer. p. 21. doi:10.1007/978-0-8176-8364-1. ISBN 978-0-8176-8363-4. https://books.google.com/books?id=3vnEcMCx0HkC&pg=PA21.
- ↑ Wohlleben, Eva (2019). "ICGG 2018 - Proceedings of the 18th International Conference on Geometry and Graphics: 40th Anniversary - Milan, Italy, August 3-7, 2018". in Cocchiarella, Luigi. International Conference on Geometry and Graphics. Springer. pp. 485–486. doi:10.1007/978-3-319-95588-9. ISBN 978-3-319-95588-9. https://books.google.com/books?id=rEpjDwAAQBAJ&pg=PA485.
External links
- Weisstein, Eric W.. "Hexagonal Pyramid". http://mathworld.wolfram.com/HexagonalPyramid.html.
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- Conway Notation for Polyhedra Try: "Y6"
- [1] Hexagonal pyramid - Polytope Wiki
 |
