Holtsmark distribution

Holtsmark

Probability density function 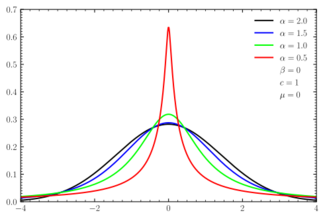Symmetric α-stable distributions with unit scale factor; α=1.5 (blue line) represents the Holtsmark distribution
Cumulative distribution function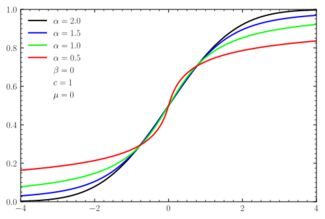
Parameters	c ∈ (0, ∞) — scale parameter μ ∈ (−∞, ∞) — location parameter
Support	x ∈ R
PDF	expressible in terms of hypergeometric functions; see text
Mean	μ
Median	μ
Mode	μ
Variance	infinite
Skewness	undefined
Kurtosis	undefined
MGF	undefined
CF	[math]\displaystyle{ \exp\left[~it\mu\!-\!|c t|^{3/2}~\right] }[/math]

The (one-dimensional) Holtsmark distribution is a continuous probability distribution. The Holtsmark distribution is a special case of a stable distribution with the index of stability or shape parameter [math]\displaystyle{ \alpha }[/math] equal to 3/2 and the skewness parameter [math]\displaystyle{ \beta }[/math] of zero. Since [math]\displaystyle{ \beta }[/math] equals zero, the distribution is symmetric, and thus an example of a symmetric alpha-stable distribution. The Holtsmark distribution is one of the few examples of a stable distribution for which a closed form expression of the probability density function is known. However, its probability density function is not expressible in terms of elementary functions; rather, the probability density function is expressed in terms of hypergeometric functions.

The Holtsmark distribution has applications in plasma physics and astrophysics. In 1919, Norwegian physicist Johan Peter Holtsmark proposed the distribution as a model for the fluctuating fields in plasma due to the motion of charged particles. It is also applicable to other types of Coulomb forces, in particular to modeling of gravitating bodies, and thus is important in astrophysics.

Characteristic function

The characteristic function of a symmetric stable distribution is:

[math]\displaystyle{ \varphi(t;\mu,c) = \exp\left[~it\mu\!-\!|c t|^\alpha~\right], }[/math]

where [math]\displaystyle{ \alpha }[/math] is the shape parameter, or index of stability, [math]\displaystyle{ \mu }[/math] is the location parameter, and c is the scale parameter.

Since the Holtsmark distribution has [math]\displaystyle{ \alpha=3/2, }[/math] its characteristic function is:

[math]\displaystyle{ \varphi(t;\mu,c) = \exp\left[~it\mu\!-\!|c t|^{3/2}~\right] . }[/math]

Since the Holtsmark distribution is a stable distribution with α > 1, [math]\displaystyle{ \mu }[/math] represents the mean of the distribution. Since β = 0, [math]\displaystyle{ \mu }[/math] also represents the median and mode of the distribution. And since α < 2, the variance of the Holtsmark distribution is infinite. All higher moments of the distribution are also infinite. Like other stable distributions (other than the normal distribution), since the variance is infinite the dispersion in the distribution is reflected by the scale parameter, c. An alternate approach to describing the dispersion of the distribution is through fractional moments.

Probability density function

In general, the probability density function, f(x), of a continuous probability distribution can be derived from its characteristic function by:

[math]\displaystyle{ f(x)=\frac{1}{2\pi}\int_{-\infty}^\infty \varphi(t)e^{-ixt}\,dt . }[/math]

Most stable distributions do not have a known closed form expression for their probability density functions. Only the normal, Cauchy and Lévy distributions have known closed form expressions in terms of elementary functions. The Holtsmark distribution is one of two symmetric stable distributions to have a known closed form expression in terms of hypergeometric functions. When [math]\displaystyle{ \mu }[/math] is equal to 0 and the scale parameter is equal to 1, the Holtsmark distribution has the probability density function:

[math]\displaystyle{ \begin{align} f(x; 0, 1) &= { 1 \over \pi }\, \Gamma\left({5 \over 3}\right) {_2F_3}\!\left({5 \over 12}, {11 \over 12}; {1 \over 3}, {1 \over 2}, {5 \over 6}; -{4x^6 \over 729}\right) \\ & {} \quad{} - { x^2 \over 3\pi }\, {_3F_4}\!\left({3 \over 4}, {1}, {5 \over 4}; {2 \over 3}, {5 \over 6}, {7 \over 6}, {4 \over 3}; -{4x^6 \over 729}\right) \\ & {} \quad{} + { 7x^4 \over 81\pi }\, \Gamma\left({4 \over 3}\right) {_2F_3}\!\left({13 \over 12}, {19 \over 12}; {7 \over 6}, {3 \over 2}, {5 \over 3}; -{4x^6 \over 729}\right), \end{align} }[/math]

where [math]\displaystyle{ {\Gamma(x)} }[/math] is the gamma function and [math]\displaystyle{ \;_mF_n() }[/math] is a hypergeometric function. One has also

[math]\displaystyle{ \begin{align} f(x; 0, 1)&=\frac{-x^2}{6\pi}\left[~_2F_2\left(1, \frac{3}{2}; \frac{4}{3}, \frac{5}{3}; -\frac{4ix^3}{27}\right)+~_2F_2\left(1, \frac{3}{2}; \frac{4}{3}, \frac{5}{3}; \frac{4ix^3}{27}\right)\right]\\ &+\frac{4}{3\times 3^{2/3}}\left[\mathrm{Bi}'\left(-\frac{x^2}{3\times 3^{1/3}}\right)\cos\left(\frac{2x^3}{27}\right)+\frac{x}{3^{2/3}}~\mathrm{Bi}\left(-\frac{x^2}{3\times 3^{1/3}}\right)\sin\left(\frac{2x^3}{27}\right)\right], \end{align} }[/math]

where [math]\displaystyle{ \mathrm{Bi} }[/math] is the Airy function of the second kind and [math]\displaystyle{ \mathrm{Bi}' }[/math] its derivative. The arguments of the [math]\displaystyle{ _2F_2 }[/math] functions are pure imaginary complex numbers, but the sum of the two functions is real. For [math]\displaystyle{ x }[/math] positive, the function [math]\displaystyle{ \mathrm{Bi}(-x) }[/math] is related to the Bessel functions of fractional order [math]\displaystyle{ J_{-1/3} }[/math] and [math]\displaystyle{ J_{1/3} }[/math] and its derivative to the Bessel functions of fractional order [math]\displaystyle{ J_{-2/3} }[/math] and [math]\displaystyle{ J_{2/3} }[/math]. Therefore, one can write

[math]\displaystyle{ \begin{align} f(x; 0, 1)&=\frac{4x^2}{27\sqrt{3}}\left\{\cos\left(\frac{2x^3}{27}\right)\left[J_{-2/3}\left(\frac{2x^3}{27}\right)+J_{2/3}\left(\frac{2x^3}{27}\right)\right]+\sin\left(\frac{2x^3}{27}\right)\left[J_{-1/3}\left(\frac{2x^3}{27}\right)-J_{1/3}\left(\frac{2x^3}{27}\right)\right]\right\}\\ &-\frac{x^2}{6\pi}\left[~_2F_2\left(1, \frac{3}{2}; \frac{4}{3}, \frac{5}{3}; -\frac{4ix^3}{27}\right)+~_2F_2\left(1, \frac{3}{2}; \frac{4}{3}, \frac{5}{3}; \frac{4ix^3}{27}\right)\right]. \end{align} }[/math]

References

• Hummer, D. G. (1986). "Rational approximations for the holtsmark distribution, its cumulative and derivative". Journal of Quantitative Spectroscopy and Radiative Transfer 36: 1–5. doi:10.1016/0022-4073(86)90011-7. Bibcode: 1986JQSRT..36....1H. https://zenodo.org/record/1253952.