Hyperrectangle

In geometry, a hyperrectangle (also called a box, hyperbox, $k$-cell or orthotope), is the generalization of a rectangle (a plane figure) and the rectangular cuboid (a solid figure) to higher dimensions. A necessary and sufficient condition is that it is congruent to the Cartesian product of finite intervals. This means that a $k$-dimensional rectangular solid has each of its edges equal to one of the closed intervals used in the definition. Every $k$-cell is compact.

If all of the edges are equal length, it is a hypercube. A hyperrectangle is a special case of a parallelotope.

Formal definition

For every integer $i$ from $1$ to $k$, let $a_i$ and $b_i$ be real numbers such that $a_i<b_i$. The set of all points $x=(x_1,\dots ,x_k)$ in ${\mathbb{ℝ}}^k$ whose coordinates satisfy the inequalities $a_i\le x_i\le b_i$ is a $k$-cell.

Intuition

A $k$-cell of dimension $k\le 3$ is especially simple. For example, a 1-cell is simply the interval $[a,b]$ with $a<b$. A 2-cell is the rectangle formed by the Cartesian product of two closed intervals, and a 3-cell is a rectangular solid.

The sides and edges of a $k$-cell need not be equal in (Euclidean) length; although the unit cube (which has boundaries of equal Euclidean length) is a 3-cell, the set of all 3-cells with equal-length edges is a strict subset of the set of all 3-cells.

Types

A four-dimensional orthotope is likely a hypercuboid.

The special case of an n-dimensional orthotope where all edges have equal length is the n-cube or hypercube.

By analogy, the term "hyperrectangle" can refer to Cartesian products of orthogonal intervals of other kinds, such as ranges of keys in database theory or ranges of integers, rather than real numbers.

Dual polytope

n-fusil
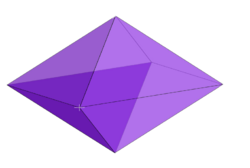Example: 3-fusil
Type	Prism
Faces	2n
Vertices	2n
Schläfli symbol	{}+{}+···+{} = n{}
Coxeter diagram	...
Symmetry group	[2n−1], order 2n
Dual polyhedron	n-orthotope
Properties	convex, isotopal

The dual polytope of an n-orthotope has been variously called a rectangular n-orthoplex, rhombic n-fusil, or n-lozenge. It is constructed by 2n points located in the center of the orthotope rectangular faces.

An n-fusil's Schläfli symbol can be represented by a sum of n orthogonal line segments: { } + { } + ... + { } or n{ }.

A 1-fusil is a line segment. A 2-fusil is a rhombus. Its plane cross selections in all pairs of axes are rhombi.

n	Example image
1	160px Line segment { }
2	160px Rhombus { } + { } = 2{ }
3	160px Rhombic 3-orthoplex inside 3-orthotope { } + { } + { } = 3{ }

See also

• Minimum bounding rectangle
• Cuboid
• Hilbert cube

References

• Coxeter, Harold Scott MacDonald (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123. ISBN 0-486-61480-8. 

External links

• Weisstein, Eric W.. "Orthotope". http://mathworld.wolfram.com/Orthotope.html. 
• Foran, James (1991-01-07). Fundamentals of Real Analysis. CRC Press. ISBN 9780824784539. https://books.google.com/books?id=sDjz8x0hJ44C&pg=PA24. Retrieved 23 May 2014. 
• Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill.