Hypograph (mathematics)
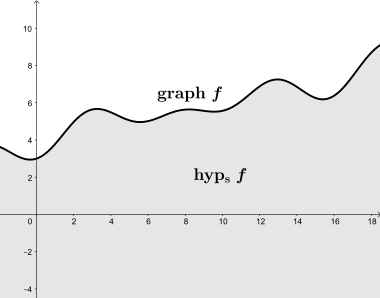
In mathematics, the hypograph or subgraph of a function [math]\displaystyle{ f:\R^{n}\rightarrow \R }[/math] is the set of points lying on or below its graph. A related definition is that of such a function's epigraph, which is the set of points on or above the function's graph.
The domain (rather than the codomain) of the function is not particularly important for this definition; it can be an arbitrary set[1] instead of [math]\displaystyle{ \mathbb{R}^n }[/math].
Definition
The definition of the hypograph was inspired by that of the graph of a function, where the graph of [math]\displaystyle{ f : X \to Y }[/math] is defined to be the set
- [math]\displaystyle{ \operatorname{graph} f := \left\{ (x, y) \in X \times Y ~:~ y = f(x) \right\}. }[/math]
The hypograph or subgraph of a function [math]\displaystyle{ f : X \to [-\infty, \infty] }[/math] valued in the extended real numbers [math]\displaystyle{ [-\infty, \infty] = \mathbb{R} \cup \{ \pm \infty \} }[/math] is the set[2]
- [math]\displaystyle{ \begin{alignat}{4} \operatorname{hyp} f &= \left\{ (x, r) \in X \times \mathbb{R} ~:~ r \leq f(x) \right\} \\ &= \left[ f^{-1}(\infty) \times \mathbb{R} \right] \cup \bigcup_{x \in f^{-1}(\mathbb{R})} \{ x \} \times (-\infty, f(x)]. \end{alignat} }[/math]
Similarly, the set of points on or above the function is its epigraph. The strict hypograph is the hypograph with the graph removed:
- [math]\displaystyle{ \begin{alignat}{4} \operatorname{hyp}_S f &= \left\{ (x, r) \in X \times \mathbb{R} ~:~ r \lt f(x) \right\} \\ &= \operatorname{hyp} f \setminus \operatorname{graph} f \\ &= \bigcup_{x \in X} \{ x \} \times (-\infty, f(x)). \end{alignat} }[/math]
Despite the fact that [math]\displaystyle{ f }[/math] might take one (or both) of [math]\displaystyle{ \pm \infty }[/math] as a value (in which case its graph would not be a subset of [math]\displaystyle{ X \times \mathbb{R} }[/math]), the hypograph of [math]\displaystyle{ f }[/math] is nevertheless defined to be a subset of [math]\displaystyle{ X \times \mathbb{R} }[/math] rather than of [math]\displaystyle{ X \times [-\infty, \infty]. }[/math]
Properties
The hypograph of a function [math]\displaystyle{ f }[/math] is empty if and only if [math]\displaystyle{ f }[/math] is identically equal to negative infinity.
A function is concave if and only if its hypograph is a convex set. The hypograph of a real affine function [math]\displaystyle{ g : \mathbb{R}^n \to \mathbb{R} }[/math] is a halfspace in [math]\displaystyle{ \mathbb{R}^{n+1}. }[/math]
A function is upper semicontinuous if and only if its hypograph is closed.
See also
Citations
- ↑ Charalambos D. Aliprantis; Kim C. Border (2007). Infinite Dimensional Analysis: A Hitchhiker's Guide (3rd ed.). Springer Science & Business Media. pp. 8–9. ISBN 978-3-540-32696-0. https://books.google.com/books?id=4hIq6ExH7NoC&pg=PA8.
- ↑ Rockafellar & Wets 2009, pp. 1-37.
References
 |