Domain of a function
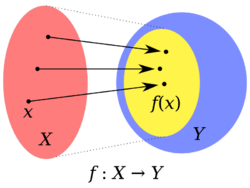
In mathematics, the domain of a function is the set of inputs accepted by the function. It is sometimes denoted by [math]\displaystyle{ \operatorname{dom}(f) }[/math] or [math]\displaystyle{ \operatorname{dom }f }[/math], where f is the function. In layman's terms, the domain of a function can generally be thought of as "what x can be".[1]
More precisely, given a function [math]\displaystyle{ f\colon X\to Y }[/math], the domain of f is X. In modern mathematical language, the domain is part of the definition of a function rather than a property of it.
In the special case that X and Y are both sets of real numbers, the function f can be graphed in the Cartesian coordinate system. In this case, the domain is represented on the x-axis of the graph, as the projection of the graph of the function onto the x-axis.
For a function [math]\displaystyle{ f\colon X\to Y }[/math], the set Y is called the codomain, and the set of values attained by the function (which is a subset of Y) is called its range or image.
Any function can be restricted to a subset of its domain. The restriction of [math]\displaystyle{ f \colon X \to Y }[/math] to [math]\displaystyle{ A }[/math], where [math]\displaystyle{ A\subseteq X }[/math], is written as [math]\displaystyle{ \left. f \right|_A \colon A \to Y }[/math].
Natural domain
If a real function f is given by a formula, it may be not defined for some values of the variable. In this case, it is a partial function, and the set of real numbers on which the formula can be evaluated to a real number is called the natural domain or domain of definition of f. In many contexts, a partial function is called simply a function, and its natural domain is called simply its domain.
Examples
- The function [math]\displaystyle{ f }[/math] defined by [math]\displaystyle{ f(x)=\frac{1}{x} }[/math] cannot be evaluated at 0. Therefore, the natural domain of [math]\displaystyle{ f }[/math] is the set of real numbers excluding 0, which can be denoted by [math]\displaystyle{ \mathbb{R} \setminus \{ 0 \} }[/math] or [math]\displaystyle{ \{x\in\mathbb R:x\ne 0\} }[/math].
- The piecewise function [math]\displaystyle{ f }[/math] defined by [math]\displaystyle{ f(x) = \begin{cases} 1/x&x\not=0\\ 0&x=0 \end{cases}, }[/math] has as its natural domain the set [math]\displaystyle{ \mathbb{R} }[/math] of real numbers.
- The square root function [math]\displaystyle{ f(x)=\sqrt x }[/math] has as its natural domain the set of non-negative real numbers, which can be denoted by [math]\displaystyle{ \mathbb R_{\geq 0} }[/math], the interval [math]\displaystyle{ [0,\infty) }[/math], or [math]\displaystyle{ \{x\in\mathbb R:x\geq 0\} }[/math].
- The tangent function, denoted [math]\displaystyle{ \tan }[/math], has as its natural domain the set of all real numbers which are not of the form [math]\displaystyle{ \tfrac{\pi}{2} + k \pi }[/math] for some integer [math]\displaystyle{ k }[/math], which can be written as [math]\displaystyle{ \mathbb R \setminus \{\tfrac{\pi}{2}+k\pi: k\in\mathbb Z\} }[/math].
Other uses
The term domain is also commonly used in a different sense in mathematical analysis: a domain is a non-empty connected open set in a topological space. In particular, in real and complex analysis, a domain is a non-empty connected open subset of the real coordinate space [math]\displaystyle{ \R^n }[/math] or the complex coordinate space [math]\displaystyle{ \C^n. }[/math]
Sometimes such a domain is used as the domain of a function, although functions may be defined on more general sets. The two concepts are sometimes conflated as in, for example, the study of partial differential equations: in that case, a domain is the open connected subset of [math]\displaystyle{ \R^{n} }[/math] where a problem is posed, making it both an analysis-style domain and also the domain of the unknown function(s) sought.
Set theoretical notions
For example, it is sometimes convenient in set theory to permit the domain of a function to be a proper class X, in which case there is formally no such thing as a triple (X, Y, G). With such a definition, functions do not have a domain, although some authors still use it informally after introducing a function in the form f: X → Y.[2]
See also
- Argument of a function
- Attribute domain
- Bijection, injection and surjection
- Codomain
- Domain decomposition
- Effective domain
- Image (mathematics)
- Lipschitz domain
- Naive set theory
- Range of a function
- Support (mathematics)
Notes
- ↑ "Domain, Range, Inverse of Functions" (in en). https://www.easysevens.com/domain-range-inverse-of-functions/.
- ↑ Eccles 1997, p. 91 (quote 1, quote 2); Mac Lane 1998, p. 8; Mac Lane, in Scott & Jech 1971, p. 232; Sharma 2010, p. 91; Stewart & Tall 1977, p. 89
References
- Bourbaki, Nicolas (1970). Théorie des ensembles. Éléments de mathématique. Springer. ISBN 9783540340348.
- Eccles, Peter J. (11 December 1997) (in en). An Introduction to Mathematical Reasoning: Numbers, Sets and Functions. Cambridge University Press. ISBN 978-0-521-59718-0. https://books.google.com/books?id=ImCSX_gm40oC.
- Mac Lane, Saunders (25 September 1998) (in en). Categories for the Working Mathematician. Springer Science & Business Media. ISBN 978-0-387-98403-2. https://books.google.com/books?id=MXboNPdTv7QC.
- Scott, Dana S.; Jech, Thomas J. (31 December 1971) (in en). Axiomatic Set Theory, Part 1. American Mathematical Soc.. ISBN 978-0-8218-0245-8. https://books.google.com/books?id=5mf4Vckj0gEC.
- Sharma, A. K. (2010) (in en). Introduction To Set Theory. Discovery Publishing House. ISBN 978-81-7141-877-0. https://books.google.com/books?id=IGvDpe6hYiQC.
- Stewart, Ian; Tall, David (1977) (in en). The Foundations of Mathematics. Oxford University Press. ISBN 978-0-19-853165-4. https://books.google.com/books?id=TLelvnIU2sEC.
 |