Indifference graph

From HandWiki
Short description: Intersection graph of unit intervals on the real number line
An indifference graph, formed from a set of points on the real line by connecting pairs of points whose distance is at most one

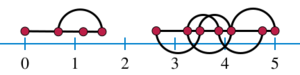
In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other.[1] Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals (intervals none of which contains any other one). Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.

Equivalent characterizations

Forbidden induced subgraphs for the indifference graphs: the claw, sun, and net (top, left–right) and cycles of length four or more (bottom)

The finite indifference graphs may be equivalently characterized as

  • The intersection graphs of unit intervals,[1]
  • The intersection graphs of sets of intervals no two of which are nested (one containing the other),[1][2]
  • The claw-free interval graphs,[1][2]
  • The graphs that do not have an induced subgraph isomorphic to a claw K1,3, net (a triangle with a degree-one vertex adjacent to each of the triangle vertices), sun (a triangle surrounded by three other triangles that each share one edge with the central triangle), or hole (cycle of length four or more),[3]
  • The incomparability graphs of semiorders,[1]
  • The undirected graphs that have a linear order such that, for every three vertices ordered [math]\displaystyle{ u }[/math]–[math]\displaystyle{ v }[/math]–[math]\displaystyle{ w }[/math], if [math]\displaystyle{ uw }[/math] is an edge then so are [math]\displaystyle{ uv }[/math] and [math]\displaystyle{ vw }[/math][4]
  • The graphs with no astral triple, three vertices connected pairwise by paths that avoid the third vertex and also do not contain two consecutive neighbors of the third vertex,[5]
  • The graphs in which each connected component contains a path in which each maximal clique of the component forms a contiguous sub-path,[6]
  • The graphs whose vertices can be numbered in such a way that every shortest path forms a monotonic sequence,[6]
  • The graphs whose adjacency matrices can be ordered such that, in each row and each column, the nonzeros of the matrix form a contiguous interval adjacent to the main diagonal of the matrix.[7]
  • The induced subgraphs of powers of chordless paths.[8]
  • The leaf powers having a leaf root which is a caterpillar.[8]

For infinite graphs, some of these definitions may differ.

Properties

Because they are special cases of interval graphs, indifference graphs have all the properties of interval graphs; in particular they are a special case of the chordal graphs and of the perfect graphs. They are also a special case of the circle graphs, something that is not true of interval graphs more generally.

In the Erdős–Rényi model of random graphs, an [math]\displaystyle{ n }[/math]-vertex graph whose number of edges is significantly less than [math]\displaystyle{ n^{2/3} }[/math] will be an indifference graph with high probability, whereas a graph whose number of edges is significantly more than [math]\displaystyle{ n^{2/3} }[/math] will not be an indifference graph with high probability.[9]

The bandwidth of an arbitrary graph [math]\displaystyle{ G }[/math] is one less than the size of the maximum clique in an indifference graph that contains [math]\displaystyle{ G }[/math] as a subgraph and is chosen to minimize the size of the maximum clique.[10] This property parallels similar relations between pathwidth and interval graphs, and between treewidth and chordal graphs. A weaker notion of width, the clique-width, may be arbitrarily large on indifference graphs.[11] However, every proper subclass of the indifference graphs that is closed under induced subgraphs has bounded clique-width.[12]

Every connected indifference graph has a Hamiltonian path.[13] An indifference graph has a Hamiltonian cycle if and only if it is biconnected.[14]

Indifference graphs obey the reconstruction conjecture: they are uniquely determined by their vertex-deleted subgraphs.[15]

Algorithms

As with higher dimensional unit disk graphs, it is possible to transform a set of points into their indifference graph, or a set of unit intervals into their unit interval graph, in linear time as measured in terms of the size of the output graph. The algorithm rounds the points (or interval centers) down to the nearest smaller integer, uses a hash table to find all pairs of points whose rounded integers are within one of each other (the fixed-radius near neighbors problem), and filters the resulting list of pairs for the ones whose unrounded values are also within one of each other.[16]

It is possible to test whether a given graph is an indifference graph in linear time, by using PQ trees to construct an interval representation of the graph and then testing whether a vertex ordering derived from this representation satisfies the properties of an indifference graph.[4] It is also possible to base a recognition algorithm for indifference graphs on chordal graph recognition algorithms.[14] Several alternative linear time recognition algorithms are based on breadth-first search or lexicographic breadth-first search rather than on the relation between indifference graphs and interval graphs.[17][18][19][20]

Once the vertices have been sorted by the numerical values that describe an indifference graph (or by the sequence of unit intervals in an interval representation) the same ordering can be used to find an optimal graph coloring for these graphs, to solve the shortest path problem, and to construct Hamiltonian paths and maximum matchings, all in linear time.[4] A Hamiltonian cycle can be found from a proper interval representation of the graph in time [math]\displaystyle{ O(n\log n) }[/math],[13] but when the graph itself is given as input, the same problem admits linear-time solution that can be generalized to interval graphs.[21][22]

List coloring remains NP-complete even when restricted to indifference graphs.[23] However, it is fixed-parameter tractable when parameterized by the total number of colors in the input.[12]

Applications

In mathematical psychology, indifference graphs arise from utility functions, by scaling the function so that one unit represents a difference in utilities small enough that individuals can be assumed to be indifferent to it. In this application, pairs of items whose utilities have a large difference may be partially ordered by the relative order of their utilities, giving a semiorder.[1][24]

In bioinformatics, the problem of augmenting a colored graph to a properly colored unit interval graph can be used to model the detection of false negatives in DNA sequence assembly from complete digests.[25]

See also

  • Threshold graph, a graph whose edges are determined by sums of vertex labels rather than differences of labels
  • Trivially perfect graph, interval graphs for which every pair of intervals is nested or disjoint rather than properly intersecting
  • Unit disk graph, a two-dimensional analogue of the indifference graphs

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 "Indifference graphs", Proof Techniques in Graph Theory (Proc. Second Ann Arbor Graph Theory Conf., Ann Arbor, Mich., 1968), Academic Press, New York, 1969, pp. 139–146 .
  2. ↑ 2.0 2.1 Bogart, Kenneth P. (1999), "A short proof that "proper = unit"", Discrete Mathematics 201 (1-3): 21–23, doi:10.1016/S0012-365X(98)00310-0 .
  3. ↑ Wegner, G. (1967), Eigenschaften der Nerven homologisch-einfacher Familien im Rn, Ph.D. thesis, Göttingen, Germany: Göttingen University . As cited by (Hell Huang).
  4. ↑ 4.0 4.1 4.2 Looges, Peter J.; Olariu, Stephan (1993), "Optimal greedy algorithms for indifference graphs", Computers & Mathematics with Applications 25 (7): 15–25, doi:10.1016/0898-1221(93)90308-I .
  5. ↑ Jackowski, Zygmunt (1992), "A new characterization of proper interval graphs", Discrete Mathematics 105 (1-3): 103–109, doi:10.1016/0012-365X(92)90135-3 .
  6. ↑ 6.0 6.1 Gutierrez, M.; Oubiña, L. (1996), "Metric characterizations of proper interval graphs and tree-clique graphs", Journal of Graph Theory 21 (2): 199–205, doi:10.1002/(SICI)1097-0118(199602)21:2<199::AID-JGT9>3.0.CO;2-M .
  7. ↑ Mertzios, George B. (2008), "A matrix characterization of interval and proper interval graphs", Applied Mathematics Letters 21 (4): 332–337, doi:10.1016/j.aml.2007.04.001 .
  8. ↑ 8.0 8.1 Brandstädt, Andreas; Hundt, Christian; Mancini, Federico; Wagner, Peter (2010), "Rooted directed path graphs are leaf powers", Discrete Mathematics 310: 897–910, doi:10.1016/j.disc.2009.10.006 .
  9. ↑ Cohen, Joel E. (1982), "The asymptotic probability that a random graph is a unit interval graph, indifference graph, or proper interval graph", Discrete Mathematics 40 (1): 21–24, doi:10.1016/0012-365X(82)90184-4 .
  10. ↑ Kaplan, Haim; Shamir, Ron (1996), "Pathwidth, bandwidth, and completion problems to proper interval graphs with small cliques", SIAM Journal on Computing 25 (3): 540–561, doi:10.1137/S0097539793258143 .
  11. ↑ "The clique-width of unit interval graphs is unbounded", Proceedings of the Thirtieth Southeastern International Conference on Combinatorics, Graph Theory, and Computing (Boca Raton, FL, 1999), Congressus Numerantium, 140, 1999, pp. 5–17 .
  12. ↑ 12.0 12.1 Lozin, Vadim V. (2008), "From tree-width to clique-width: excluding a unit interval graph", Algorithms and computation, Lecture Notes in Comput. Sci., 5369, Springer, Berlin, pp. 871–882, doi:10.1007/978-3-540-92182-0_76 .
  13. ↑ 13.0 13.1 Bertossi, Alan A. (1983), "Finding Hamiltonian circuits in proper interval graphs", Information Processing Letters 17 (2): 97–101, doi:10.1016/0020-0190(83)90078-9 .
  14. ↑ 14.0 14.1 Panda, B. S.; Das, Sajal K. (2003), "A linear time recognition algorithm for proper interval graphs", Information Processing Letters 87 (3): 153–161, doi:10.1016/S0020-0190(03)00298-9 .
  15. ↑ von Rimscha, Michael (1983), "Reconstructibility and perfect graphs", Discrete Mathematics 47 (2-3): 283–291, doi:10.1016/0012-365X(83)90099-7 .
  16. ↑ "The complexity of finding fixed-radius near neighbors", Information Processing Letters 6 (6): 209–212, 1977, doi:10.1016/0020-0190(77)90070-9 .
  17. ↑ "Simple linear time recognition of unit interval graphs", Information Processing Letters 55 (2): 99–104, 1995, doi:10.1016/0020-0190(95)00046-F .
  18. ↑ Herrera de Figueiredo, Celina M.; Meidanis, João; Picinin de Mello, Célia (1995), "A linear-time algorithm for proper interval graph recognition", Information Processing Letters 56 (3): 179–184, doi:10.1016/0020-0190(95)00133-W .
  19. ↑ "A simple 3-sweep LBFS algorithm for the recognition of unit interval graphs", Discrete Applied Mathematics 138 (3): 371–379, 2004, doi:10.1016/j.dam.2003.07.001 .
  20. ↑ "Certifying LexBFS recognition algorithms for proper interval graphs and proper interval bigraphs", SIAM Journal on Discrete Mathematics 18 (3): 554–570, 2004, doi:10.1137/S0895480103430259 .
  21. ↑ Keil, J. Mark (1985), "Finding Hamiltonian circuits in interval graphs", Information Processing Letters 20 (4): 201–206, doi:10.1016/0020-0190(85)90050-X .
  22. ↑ Ibarra, Louis (2009), "A simple algorithm to find Hamiltonian cycles in proper interval graphs", Information Processing Letters 109 (18): 1105–1108, doi:10.1016/j.ipl.2009.07.010 .
  23. ↑ Marx, Dániel (2006), "Precoloring extension on unit interval graphs", Discrete Applied Mathematics 154 (6): 995–1002, doi:10.1016/j.dam.2005.10.008 .
  24. ↑ "On nontransitive indifference", Journal of Mathematical Psychology 7: 243–258, 1970, doi:10.1016/0022-2496(70)90047-7 .
  25. ↑ Goldberg, Paul W.; Golumbic, Martin C.; Kaplan, Haim; Shamir, Ron (2009), "Four strikes against physical mapping of DNA", Journal of Computational Biology 2 (2), doi:10.1089/cmb.1995.2.139, PMID 7497116 .

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Indifference_graph&oldid=3361784"