Utility
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings.
- In a normative context, utility refers to a goal or objective that we wish to maximize, i.e., an objective function. This kind of utility bears a closer resemblance to the original utilitarian concept, developed by moral philosophers such as Jeremy Bentham and John Stuart Mill.
- In a descriptive context, the term refers to an apparent objective function; such a function is revealed by a person's behavior, and specifically by their preferences over lotteries, which can be any quantified choice.
The relationship between these two kinds of utility functions has been a source of controversy among both economists and ethicists, with most maintaining that the two are distinct but generally related.
Utility function
Consider a set of alternatives among which a person has a preference ordering. A utility function represents that ordering if it is possible to assign a real number to each alternative in such a manner that alternative a is assigned a number greater than alternative b if and only if the individual prefers alternative a to alternative b. In this situation, someone who selects the most preferred alternative must also choose one that maximizes the associated utility function.
Suppose James has utility function such that is the number of apples and is the number of chocolates. Alternative A has apples and chocolates; alternative B has apples and chocolates. Putting the values into the utility function yields for alternative A and for B, so James prefers alternative B. In general economic terms, a utility function ranks preferences concerning a set of goods and services.
Gérard Debreu derived the conditions required for a preference ordering to be representable by a utility function.[1] For a finite set of alternatives, these require only that the preference ordering is complete (so the individual can determine which of any two alternatives is preferred or that they are indifferent), and that the preference order is transitive.
Suppose the set of alternatives is not finite (for example, even if the number of goods is finite, the quantity chosen can be any real number on an interval). In that case, a continuous utility function exists representing a consumer's preferences if and only if the consumer's preferences are complete, transitive, and continuous.[2]
Applications
Utility can be represented through sets of indifference curve, which are level curves of the function itself and which plot the combination of commodities that an individual would accept to maintain a given level of satisfaction. Combining indifference curves with budget constraints allows for individual demand curves derivation.

In an indifference curve, the vertical and horizontal axes represent an individual's consumption of commodity Y and X respectively. All the combinations of commodity X and Y along the same indifference curve are regarded indifferently by individuals, which means all the combinations along an indifference curve result in the same utility value.
Individual and social utility can be construed as the value of a utility function and a social welfare function, respectively. When coupled with production or commodity constraints, by some assumptions, these functions can be used to analyze Pareto efficiency, such as illustrated by Edgeworth boxes in contract curves. Such efficiency is a major concept in welfare economics.
Preference
While preferences are the conventional foundation of choice theory in microeconomics, it is often convenient to represent preferences with a utility function. Let X be the consumption set, the set of all mutually exclusive baskets the consumer could consume. The consumer's utility function ranks each possible outcome in the consumption set. If the consumer strictly prefers x to y or is indifferent between them, then .
For example, suppose a consumer's consumption set is X = {nothing, 1 apple,1 orange, 1 apple and 1 orange, 2 apples, 2 oranges}, and his utility function is u(nothing) = 0, u(1 apple) = 1, u(1 orange) = 2, u(1 apple and 1 orange) = 5, u(2 apples) = 2 and u(2 oranges) = 4. Then this consumer prefers 1 orange to 1 apple but prefers one of each to 2 oranges.
In micro-economic models, there is usually a finite set of L commodities, and a consumer may consume an arbitrary amount of each commodity. This gives a consumption set of , and each package is a vector containing the amounts of each commodity. For the example, there are two commodities: apples and oranges. If we say apples are the first commodity, and oranges the second, then the consumption set is and u(0, 0) = 0, u(1, 0) = 1, u(0, 1) = 2, u(1, 1) = 5, u(2, 0) = 2, u(0, 2) = 4 as before. For u to be a utility function on X, however, it must be defined for every package in X, so now the function must be defined for fractional apples and oranges too. One function that would fit these numbers is
Preferences have three main properties:
- Completeness
Assume an individual has two choices, A and B. By ranking the two choices, one and only one of the following relationships is true: an individual strictly prefers A (A > B); an individual strictly prefers B (B>A); an individual is indifferent between A and B (A = B). Either a ≥ b OR b ≥ a (OR both) for all (a,b)
- Transitivity
Individuals' preferences are consistent over bundles. If an individual prefers bundle A to bundle B and bundle B to bundle C, then it can be assumed that the individual prefers bundle A to bundle C. (If a ≥ b and b ≥ c, then a ≥ c for all (a,b,c)).
- Non-satiation or monotonicity
If bundle A contains all the goods that a bundle B contains, but A also includes more of at least one good than B. The individual prefers A over B.[3] If, for example, bundle A = {1 apple,2 oranges}, and bundle B = {1 apple,1 orange}, then A is preferred over B.
Revealed preference
It was recognized that utility could not be measured or observed directly, so instead economists devised a way to infer relative utilities from observed choice. These 'revealed preferences', as termed by Paul Samuelson, were revealed e.g. in people's willingness to pay:
Utility is assumed to be correlative to Desire or Want. It has been argued already that desires cannot be measured directly, but only indirectly, by the outward phenomena which they cause: and that in those cases with which economics is mainly concerned the measure is found by the price which a person is willing to pay for the fulfillment or satisfaction of his desire.[4]: 78
Functions
Utility functions, expressing utility as a function of the amounts of the various goods consumed, are treated as either cardinal or ordinal, depending on whether they are or are not interpreted as providing more information than simply the rank ordering of preferences among bundles of goods, such as information concerning the strength of preferences.
Cardinal
Cardinal utility states that the utilities obtained from consumption can be measured and ranked objectively and are representable by numbers.[5] There are fundamental assumptions of cardinal utility. Economic agents should be able to rank different bundles of goods based on their preferences or utilities and sort different transitions between two bundles of goods.[6]
A cardinal utility function can be transformed to another utility function by a positive linear transformation (multiplying by a positive number, and adding some other number); however, both utility functions represent the same preferences.[7]
When cardinal utility is assumed, the magnitude of utility differences is treated as an ethically or behaviorally significant quantity. For example, suppose a cup of orange juice has utility of 120 "utils", a cup of tea has a utility of 80 utils, and a cup of water has a utility of 40 utils. With cardinal utility, it can be concluded that the cup of orange juice is better than the cup of tea by the same amount by which the cup of tea is better than the cup of water. This means that if a person has a cup of tea, they would be willing to take any bet with a probability, p, greater than .5 of getting a cup of juice, with a risk of getting a cup of water equal to 1-p. One cannot conclude, however, that the cup of tea is two-thirds of the goodness of the cup of juice because this conclusion would depend not only on magnitudes of utility differences but also on the "zero" of utility. For example, if the "zero" of utility were located at -40, then a cup of orange juice would be 160 utils more than zero, a cup of tea 120 utils more than zero. Cardinal utility can be considered as the assumption that quantifiable characteristics, such as height, weight, temperature, etc can measure utility.
Neoclassical economics has largely retreated from using cardinal utility functions as the basis of economic behavior. A notable exception is in the context of analyzing choice with conditions of risk (see below).
Sometimes cardinal utility is used to aggregate utilities across persons, to create a social welfare function.
Ordinal
Instead of giving actual numbers over different bundles, ordinal utilities are only the rankings of utilities received from different bundles of goods or services.[5] For example, ordinal utility could tell that having two ice creams provide a greater utility to individuals in comparison to one ice cream but could not tell exactly how much extra utility received by the individual. Ordinal utility, it does not require individuals to specify how much extra utility they received from the preferred bundle of goods or services in comparison to other bundles. They are only needed to tell which bundles they prefer.
When ordinal utilities are used, differences in utils (values assumed by the utility function) are treated as ethically or behaviorally meaningless: the utility index encodes a full behavioral ordering between members of a choice set, but tells nothing about the related strength of preferences. For the above example, it would only be possible to say that juice is preferred to tea to water. Thus, ordinal utility utilizes comparisons, such as "preferred to", "no more", "less than", etc.
If a function is ordinal and non-negative, it is equivalent to the function , because taking the square is an increasing monotone (or monotonic) transformation. This means that the ordinal preference induced by these functions is the same (although they are two different functions). In contrast, if is cardinal, it is not equivalent to .
Examples
In order to simplify calculations, various alternative assumptions have been made concerning details of human preferences, and these imply various alternative utility functions such as:
- CES (constant elasticity of substitution).
- Isoelastic utility
- Exponential utility
- Quasilinear utility
- Homothetic preferences
- Stone–Geary utility function
- Gorman polar form
- Hyperbolic absolute risk aversion
Most utility functions used for modeling or theory are well-behaved. They are usually monotonic and quasi-concave. However, it is possible for rational preferences not to be representable by a utility function. An example is lexicographic preferences which are not continuous and cannot be represented by a continuous utility function.[8]
Marginal utility
Economists distinguish between total utility and marginal utility. Total utility is the utility of an alternative, an entire consumption bundle or situation in life. The rate of change of utility from changing the quantity of one good consumed is termed the marginal utility of that good. Marginal utility therefore measures the slope of the utility function with respect to the changes of one good.[9] Marginal utility usually decreases with consumption of the good, the idea of "diminishing marginal utility". In calculus notation, the marginal utility of good X is . When a good's marginal utility is positive, additional consumption of it increases utility; if zero, the consumer is satiated and indifferent about consuming more; if negative, the consumer would pay to reduce his consumption.[10]
Law of diminishing marginal utility
Rational individuals only consume additional units of goods if it increases the marginal utility. However, the law of diminishing marginal utility means an additional unit consumed brings a lower marginal utility than that carried by the previous unit consumed. For example, drinking one bottle of water makes a thirsty person satisfied; as the consumption of water increases, he may feel begin to feel bad which causes the marginal utility to decrease to zero or even become negative. Furthermore, this is also used to analyze progressive taxes as the greater taxes can result in the loss of utility.
Marginal rate of substitution (MRS)
Marginal rate of substitution is the absolute value of the slope of the indifference curve, which measures how much an individual is willing to switch from one good to another. Using a mathematic equation, keeping U(x1,x2) constant. Thus, MRS is how much an individual is willing to pay for consuming a greater amount of x1.
MRS is related to marginal utility. The relationship between marginal utility and MRS is:[9]
Expected utility
Expected utility theory deals with the analysis of choices among risky projects with multiple (possibly multidimensional) outcomes.
The St. Petersburg paradox was first proposed by Nicholas Bernoulli in 1713 and solved by Daniel Bernoulli in 1738, although the Swiss mathematician Gabriel Cramer proposed taking the expectation of a square-root utility function of money in an 1728 letter to N. Bernoulli. D. Bernoulli argued that the paradox could be resolved if decision-makers displayed risk aversion and argued for a logarithmic cardinal utility function. (Analysis of international survey data during the 21st century has shown that insofar as utility represents happiness, as for utilitarianism, it is indeed proportional to log of income.)
The first important use of the expected utility theory was that of John von Neumann and Oskar Morgenstern, who used the assumption of expected utility maximization in their formulation of game theory.
In finding the probability-weighted average of the utility from each possible outcome:
Von Neumann–Morgenstern
Von Neumann and Morgenstern addressed situations in which the outcomes of choices are not known with certainty, but have probabilities associated with them.
A notation for a lottery is as follows: if options A and B have probability p and 1 − p in the lottery, we write it as a linear combination:
More generally, for a lottery with many possible options:
where .
By making some reasonable assumptions about the way choices behave, von Neumann and Morgenstern showed that if an agent can choose between the lotteries, then this agent has a utility function such that the desirability of an arbitrary lottery can be computed as a linear combination of the utilities of its parts, with the weights being their probabilities of occurring.
This is termed the expected utility theorem. The required assumptions are four axioms about the properties of the agent's preference relation over 'simple lotteries', which are lotteries with just two options. Writing to mean 'A is weakly preferred to B' ('A is preferred at least as much as B'), the axioms are:
- completeness: For any two simple lotteries and , either or (or both, in which case they are viewed as equally desirable).
- transitivity: for any three lotteries , if and , then .
- convexity/continuity (Archimedean property): If , then there is a between 0 and 1 such that the lottery is equally desirable as .
- independence: for any three lotteries and any probability p, if and only if . Intuitively, if the lottery formed by the probabilistic combination of and is no more preferable than the lottery formed by the same probabilistic combination of and then and only then .
Axioms 3 and 4 enable us to decide about the relative utilities of two assets or lotteries.
In more formal language: A von Neumann–Morgenstern utility function is a function from choices to the real numbers:
which assigns a real number to every outcome in a way that represents the agent's preferences over simple lotteries. Using the four assumptions mentioned above, the agent will prefer a lottery to a lottery if and only if, for the utility function characterizing that agent, the expected utility of is greater than the expected utility of :
- .
Of all the axioms, independence is the most often discarded. A variety of generalized expected utility theories have arisen, most of which omit or relax the independence axiom.
Indirect utility
An indirect utility function gives the optimal attainable value of a given utility function, which depends on the prices of the goods and the income or wealth level that the individual possesses.
Money
One use of the indirect utility concept is the notion of the utility of money. The (indirect) utility function for money is a nonlinear function that is bounded and asymmetric about the origin. The utility function is concave in the positive region, representing the phenomenon of diminishing marginal utility. The boundedness represents the fact that beyond a certain amount money ceases being useful at all, as the size of any economy at that time is itself bounded. The asymmetry about the origin represents the fact that gaining and losing money can have radically different implications both for individuals and businesses. The non-linearity of the utility function for money has profound implications in decision-making processes: in situations where outcomes of choices influence utility by gains or losses of money, which are the norm for most business settings, the optimal choice for a given decision depends on the possible outcomes of all other decisions in the same time-period.[11]
Budget constraints
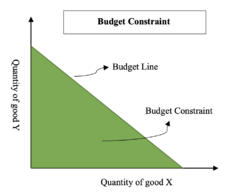
Individuals' consumptions are constrained by their budget allowance. The graph of budget line is a linear, downward-sloping line between X and Y axes. All the bundles of consumption under the budget line allow individuals to consume without using the whole budget as the total budget is greater than the total cost of bundles. If only considers prices and quantities of two goods in one bundle, a budget constraint could be formulated as , where and are prices of the two goods, and are quantities of the two goods.
Constrained utility optimisation
Rational consumers wish to maximise their utility. However, as they have budget constraints, a change of price would affect the quantity of demand. There are two factors could explain this situation:
- Purchasing power. Individuals obtain greater purchasing power when the price of a good decreases. The reduction of the price allows individuals to increase their savings so they could afford to buy other products.
- Substitution effect. If the price of good A decreases, then the good becomes relatively cheaper with respect to its substitutes. Thus, individuals would consume more of good A as the utility would increase by doing so.
Interpersonal comparisons of utility
Template:LLM The concept of interpersonal comparisons of utility refers to the evaluation of satisfaction or well-being across multiple individuals, aiming to determine the relative levels of utility (happiness or benefit) experienced by each person. This concept is widely regarded as problematic in economics, as subjective well-being lacks an objective metric, making direct measurement and comparison between individuals inherently challenging.[12]
Challenges
The primary challenge lies in the inability to directly observe or access another individual's internal thoughts and emotions, rendering it impossible to objectively determine whether one person experiences greater utility than another in a given context.[13][14]
Normative aspect
Comparing utility between individuals typically depends on subjective judgments and ethical assumptions regarding the nature of "well-being" or "happiness," making such analyses inherently normative rather than purely empirical.[14]
Applications despite limitations
Despite the inherent difficulties, certain economic theories, particularly within welfare economics, incorporate interpersonal comparisons of utility to assess the effects of policies on different population groups. However, such analyses are typically conducted with substantial caveats and methodological limitations.[15]
Types of interpersonal utility comparisons
- Utility level: Interpersonal utility comparisons are widely debated, with many economists and philosophers asserting that the inability to fully understand others' mental states renders such comparisons unreliable. A key distinction exists between comparisons of absolute utility levels and differences in utility between individuals. Utilitarianism relies on the comparability of utility differences to optimize a social welfare function, whereas Rawls’s maximin principle depends on the comparability of absolute utility levels. The extent to which interpersonal utility comparisons are considered valid is influenced by whether one adopts an ordinalist or cardinalist interpretation of utility functions.[12]
- Utility differences: Utility differences refer to the measurable variations in utility levels between individuals, particularly in relation to their ability to perceive changes in well-being. Psychological studies suggest that humans have finite sensitivity, meaning small differences in utility may go unnoticed. This concept, explored by economists such as Francis Edgeworth and Jeremy Bentham, underpins the idea that a "just perceivable" change in utility can serve as a unit of comparison across individuals. The Weak Majority Preference Criterion (WMP) supports interpersonal utility comparisons by prioritizing utility differences that influence the preferences of at least half of a population. This principle leads to a utilitarian social welfare function, where social welfare is determined by the unweighted sum of individual utilities.[15]
Criticism
Utility is a subjective measure of satisfaction that differs among individuals based on personal values, experiences, and circumstances. Cultural background, psychological factors, and socio-economic conditions influence how utility is perceived. This variability complicates economic analyses, as utility cannot be objectively measured or directly compared across different individuals.[13]
It is argued that, by being inherently subjective, it is impossible to objectively quantify utility and compare individual levels of well-being. Differences in personal preferences, perceptions, and circumstances prevent the establishment of a universal measurement standard. As a result, economic theories relying on interpersonal utility comparisons face significant methodological and philosophical challenges.[13]
Some argue that making interpersonal utility comparisons can raise ethical issues if it implies that some individuals' happiness is inherently more valuable than others.[16]
Discussion and criticism
Cambridge economist Joan Robinson famously criticized utility for being a circular concept: "Utility is the quality in commodities that makes individuals want to buy them, and the fact that individuals want to buy commodities shows that they have utility".[17]: 48 Robinson also stated that because the theory assumes that preferences are fixed this means that utility is not a testable assumption. This is so because if we observe changes of peoples' behavior in relation to a change in prices or a change in budget constraint we can never be sure to what extent the change in behavior was due to the change of price or budget constraint and how much was due to a change of preference.[18] This criticism is similar to that of the philosopher Hans Albert who argued that the ceteris paribus (all else equal) conditions on which the marginalist theory of demand rested rendered the theory itself a meaningless tautology, incapable of being tested experimentally.[19] .
Other questions of what arguments ought to be included in a utility function are difficult to answer, yet seem necessary to understanding utility. Whether people gain utility from coherence of wants, beliefs or a sense of duty is important to understanding their behavior in the utility organon.[20] Likewise, choosing between alternatives is itself a process of determining what to consider as alternatives, a question of choice within uncertainty.[21]
An evolutionary psychology theory is that utility may be better considered as due to preferences that maximized evolutionary fitness in the ancestral environment but not necessarily in the current one.[22]
Measuring utility functions
There are many empirical works trying to estimate the form of utility functions of agents with respect to money.[23]
See also
- Happiness economics
- Law of demand
- Utility maximization problem - a problem faced by consumers in a market: how to maximize their utility given their budget.
- Utility assessment - processes for estimating the utility functions of human subjects.
References
- ↑ Debreu, Gérard (1954), "Representation of a preference ordering by a numerical function", Decision processes, New York: Wiley, pp. 159–167, OCLC 639321.
- ↑ Jehle, Geoffrey; Reny, Philipp (2011), Advanced Microeconomic Theory, Prentice Hall, Financial Times, pp. 13–16, ISBN 978-0-273-73191-7.
- ↑ "nonsatiation" (in en). https://www.oxfordreference.com/display/10.1093/oi/authority.20110803100237926.
- ↑ Marshall, Alfred (1920). Principles of Economics. An introductory volume (8th ed.). London: Macmillan.
- ↑ 5.0 5.1 Dominick, Salvatore (2008). Principles Of Microeconomics. New Delhi: Oxford Higher Education/Oxford University Press. pp. 60. ISBN 9780198062301.
- ↑ Lin, Chung-Cheng; Peng, Shi-Shu (2019). "The role of diminishing marginal utility in the ordinal and cardinal utility theories". Australian Economic Papers 58 (3): 233–246. doi:10.1111/1467-8454.12151. https://onlinelibrary.wiley.com/doi/abs/10.1111/1467-8454.12151.
- ↑ Moscati, Ivan (2013). "How Cardinal Utility Entered Economic Analysis, 1909-1944". SSRN Electronic Journal. doi:10.2139/ssrn.2296881. ISSN 1556-5068.
- ↑ Ingersoll, Jonathan E. Jr. (1987). Theory of Financial Decision Making. Totowa: Rowman and Littlefield. p. 21. ISBN 0-8476-7359-6. https://archive.org/details/theoryoffinancia1987inge.
- ↑ 9.0 9.1 Castro, Luiz Carvalho; Araujo, Antônio Souza (2019). "Marginal Utility & its Diminishing Methods". International Journal of Tax Economics and Management: 36–47. https://journals.seagullpublications.com/ijtem/archive/f_IJ0320191627.pdf.
- ↑ Bloomenthal, Andrew. "Marginal Utility". https://www.investopedia.com/terms/m/marginalutility.asp.
- ↑ Berger, J. O. (1985). "Utility and Loss". Statistical Decision Theory and Bayesian Analysis (2nd ed.). Berlin: Springer-Verlag. ISBN 3-540-96098-8.
- ↑ 12.0 12.1 Interpersonal Comparisons of Utility. doi:10.1057/978-1-349-95121-5_1119-2. https://link.springer.com/referenceworkentry/10.1057/978-1-349-95121-5_1119-2. Retrieved 4 February 2025.
- ↑ 13.0 13.1 13.2 Ken Binmore. "Interpersonal Comparison of Utility". https://discovery.ucl.ac.uk/id/eprint/14435/1/14435.pdf. Retrieved 4 February 2025.
- ↑ 14.0 14.1 John B. Davis (Summer 1992). "Interpretation of Interpersonal Utility Comparisons: Positive, Normative or Descriptive". https://epublications.marquette.edu/cgi/viewcontent.cgi?article=1452&context=econ_fac. Retrieved 4 February 2025.
- ↑ 15.0 15.1 Peter J. Hammond (1977). "Dual Interpersonal Comparisons of Utility and the Welfare Economics of Income Distribution". Journal of Public Economics 7 (1): 51–71. doi:10.1016/0047-2727(77)90036-6. https://www.sciencedirect.com/science/article/abs/pii/0047272777900366. Retrieved 4 February 2025.
- ↑ "Interpersonal Comparison of Utility". https://www.oxfordreference.com/display/10.1093/oi/authority.20110803100008271. Retrieved 4 February 2025.
- ↑ Robinson, Joan (1962). Economic Philosophy. Harmondsworth, Middle-sex, UK: Penguin Books.
- ↑ Pilkington, Philip (17 February 2014). "Joan Robinson's Critique of Marginal Utility Theory". Fixing the Economists. https://fixingtheeconomists.wordpress.com/2014/02/17/joan-robinsons-critique-of-marginal-utility-theory/.
- ↑ Pilkington, Philip (27 February 2014). "utility Hans Albert Expands Robinson's Critique of Marginal Utility Theory to the Law of Demand". Fixing the Economists. https://fixingtheeconomists.wordpress.com/2014/02/27/hans-albert-expands-robinsons-critique-of-marginal-utility-theory-to-the-law-of-demand/.
- ↑ Klein, Daniel (May 2014). "Professor". Econ Journal Watch 11 (2): 97–105. http://econjwatch.org/file_download/826/CompleteIssueMay2014.pdf. Retrieved November 15, 2014.
- ↑ Burke, Kenneth (1932). Towards a Better Life. Berkeley, Calif: University of California Press.
- ↑ Capra, C. Monica; Rubin, Paul H. (2011). "The Evolutionary Psychology of Economics". Applied Evolutionary Psychology. Oxford University Press. doi:10.1093/acprof:oso/9780199586073.003.0002. ISBN 9780191731358.
- ↑ Kirby, Kris N. (2011). "An empirical assessment of the form of utility functions" (in en). https://psycnet.apa.org/record/2011-03782-002.
Further reading
- Anand, Paul (1993). Foundations of Rational Choice Under Risk. Oxford University Press. ISBN 0-19-823303-5. https://archive.org/details/foundationsofrat00anan.
- Fishburn, Peter C. (1970). Utility Theory for Decision Making. Huntington, NY: Robert E. Krieger. ISBN 0-88275-736-9.
- Georgescu-Roegen, Nicholas (Aug 1936). "The Pure Theory of Consumer's Behavior". Quarterly Journal of Economics 50 (4): 545–593. doi:10.2307/1891094.
- Gilboa, Itzhak (2009). Theory of Decision under Uncertainty. Cambridge University Press. ISBN 978-0-521-74123-1.
- Kreps, David M. (1988). Notes on the Theory of Choice. Boulder, CO: West-view Press. ISBN 0-8133-7553-3.
- Nash, John F. (1950). "The Bargaining Problem". Econometrica 18 (2): 155–162. doi:10.2307/1907266.
- Neumann, John von; Morgenstern, Oskar (1944). Theory of Games and Economic Behavior. Princeton University Press. https://archive.org/details/in.ernet.dli.2015.215284.
- Nicholson, Walter (1978). Micro-economic Theory (Second ed.). Hinsdale: Dryden Press. pp. 53–87. ISBN 0-03-020831-9.
- Plous, S. (1993). The Psychology of Judgement and Decision Making. McGraw-Hill. ISBN 0-07-050477-6.
- Viner, Jacob (1925). "The Utility Concept in Value Theory and Its Critics". Journal of Political Economy. 33 (4): 369–387.
- Viner, Jacob (1925). "The Utility Concept in Value Theory and Its Critics". Journal of Political Economy. 33 (6): 638–659.
External links
- Definition of Utility by Investopedia
- Anatomy of Cobb-Douglas Type Utility Functions in 3D
- Anatomy of CES Type Utility Functions in 3D
- Simpler Definition with example from Investopedia
- Maximization of Originality - redefinition of classic utility
- Utility Model of Marketing - Form , Place , Time
, Possession and perhaps also Task
 |
