Intersection number (graph theory)

From HandWiki
Short description: Fewest cliques covering a graph's edges

In the mathematical field of graph theory, the intersection number of a graph [math]\displaystyle{ G=(V,E) }[/math] is the smallest number of elements in a representation of [math]\displaystyle{ G }[/math] as an intersection graph of finite sets. In such a representation, each vertex is represented as a set, and two vertices are connected by an edge whenever their sets have a common element. Equivalently, the intersection number is the smallest number of cliques needed to cover all of the edges of [math]\displaystyle{ G }[/math].[1][2]

A set of cliques that cover all edges of a graph is called a clique edge cover[3] or edge clique cover,[4] or even just a clique cover, although the last term is ambiguous: a clique cover can also be a set of cliques that cover all vertices of a graph.[5] Sometimes "covering" is used in place of "cover".[6] As well as being called the intersection number, the minimum number of these cliques has been called the R-content,[7] edge clique cover number,[4] or clique cover number.[8] The problem of computing the intersection number has been called the intersection number problem,[9] the intersection graph basis problem,[10] covering by cliques,[10] the edge clique cover problem,[9] and the keyword conflict problem.[2]

Every graph with [math]\displaystyle{ n }[/math] vertices and [math]\displaystyle{ m }[/math] edges has intersection number at most [math]\displaystyle{ \min(m,n^2/4) }[/math]. The intersection number is NP-hard to compute or approximate, but fixed-parameter tractable.

Definitions

Intersection graphs

Let [math]\displaystyle{ \mathcal{F} }[/math] be any family of sets, allowing sets in [math]\displaystyle{ \mathcal{F} }[/math] to be repeated. Then the intersection graph of [math]\displaystyle{ \mathcal{F} }[/math] is an undirected graph that has a vertex for each set in [math]\displaystyle{ \mathcal{F} }[/math] and an edge between each two sets that have a nonempty intersection. Every graph can be represented as an intersection graph in this way.[11] The intersection number of the graph is the smallest number [math]\displaystyle{ k }[/math] such that there exists a representation of this type for which the union of the sets in [math]\displaystyle{ \mathcal{F} }[/math] has [math]\displaystyle{ k }[/math] elements.[1] The problem of finding an intersection representation of a graph with a given number of elements is known as the intersection graph basis problem.[10]

Clique edge covers

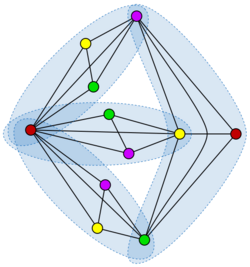
A graph with intersection number four. The four shaded regions indicate cliques that cover all the edges of the graph.

An alternative definition of the intersection number of a graph [math]\displaystyle{ G }[/math] is that it is the smallest number of cliques in [math]\displaystyle{ G }[/math] (complete subgraphs of [math]\displaystyle{ G }[/math]) that together cover all of the edges of [math]\displaystyle{ G }[/math].[1][12] A set of cliques with this property is known as a clique edge cover or edge clique cover, and for this reason the intersection number is also sometimes called the edge clique cover number.[4]

Equivalence

The equality of the intersection number and the edge clique cover number is straightforward to prove. In one direction, suppose that [math]\displaystyle{ G }[/math] is the intersection graph of a family [math]\displaystyle{ \mathcal{F} }[/math] of sets whose union [math]\displaystyle{ U }[/math] has [math]\displaystyle{ k }[/math] elements. Then for any element [math]\displaystyle{ x\in U }[/math], the subset of vertices of [math]\displaystyle{ G }[/math] corresponding to sets that contain [math]\displaystyle{ x }[/math] forms a clique: any two vertices in this subset are adjacent, because their sets have a nonempty intersection containing [math]\displaystyle{ x }[/math]. Further, every edge in [math]\displaystyle{ G }[/math] is contained in one of these cliques: if an edge comes from a non-empty intersection of sets containing an element [math]\displaystyle{ y }[/math], then that edge is contained in the clique for [math]\displaystyle{ y }[/math]. Therefore, the edges of [math]\displaystyle{ G }[/math] can be covered by [math]\displaystyle{ k }[/math] cliques, one per element of [math]\displaystyle{ U }[/math].[12]

In the other direction, if a graph [math]\displaystyle{ G }[/math] can be covered by [math]\displaystyle{ k }[/math] cliques, then each vertex [math]\displaystyle{ v }[/math] of [math]\displaystyle{ G }[/math] may be represented by a subset of the cliques, the ones that contain vertex [math]\displaystyle{ v }[/math]. Two of these subsets, for two vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math], have a nonempty intersection if and only if there is a clique in the intersection that contains both of them, if and only if there is an edge [math]\displaystyle{ uv }[/math] included in one of the covering cliques.[12]

Applications

The representation of a graph as an abstract intersection graph of sets can be used to construct more concrete geometric intersection representations of the same graph. In particular, if a graph has intersection number [math]\displaystyle{ k }[/math], it can be represented as an intersection graph of [math]\displaystyle{ k }[/math]-dimensional unit hypercubes (implying that its boxicity is at most [math]\displaystyle{ k }[/math]), or as an intersection graph of [math]\displaystyle{ k }[/math]-dimensional unit hyperspheres (its sphericity is at most [math]\displaystyle{ k }[/math]).[4]

A clique cover can be used as a kind of adjacency labelling scheme for a graph, in which one labels each vertex by a binary value with a bit for each clique, zero if it does not belong to the clique and one if it belongs. Then two vertices are adjacent if and only if the bitwise and of their labels is nonzero. The length of the labels is the intersection number of the graph. This method was used in an early application of intersection numbers, for labeling a set of keywords so that conflicting keywords could be quickly detected, by E. Kellerman of IBM. For this reason, another name for the problem of computing intersection numbers is the keyword conflict problem.[13][14] Similarly, in computational geometry, representations based on the intersection number have been considered as a compact representation for visibility graphs, but there exist geometric inputs for which this representation requires a near-quadratic number of cliques.[15]

Another class of applications comes from scheduling problems in which multiple users of a shared resource should be scheduled for time slots, in such a way that incompatible requests are never scheduled for the same time slot but all pairs of compatible requests are given at least one time slot together. The intersection number of a graph of compatibilities gives the minimum number of time slots needed for such a schedule.[2] In the design of compilers for very long instruction word computers, a small clique cover of a graph of incompatible operations can be used to represent their incompatibilities by a small number of artificial resources, allowing resource-based scheduling techniques to be used to assign operations to instruction slots.[16]

Shephard and Vetta observe that the intersection number of any network equals the minimum number of constraints needed in an integer programming formulation of the problem of computing maximum independent sets, in which one has a 0-1 variable per vertex and a constraint that in each clique of a clique cover the variables sum to at most one. They argue that, for the intersection graphs of paths in certain fiber optic communications networks, these intersection numbers are small, explaining the relative ease of solving certain optimization problems in allocating bandwidth on the networks.[3]

In statistics and data visualization, edge clique covers of a graph representing statistically indistinguishable pairs of variables are used to produce compact letter displays that assist in visualizing multiple pairwise comparisons, by assigning a letter or other visual marker for each clique and using these to provide a graphical representation of which variables are indistinguishable.[17][18]

In the analysis of food webs describing predator-prey relationships among animal species, a competition graph or niche overlap graph is an undirected graph in which the vertices represent species, and edges represent pairs of species that both compete for the same prey. These can be derived from a directed acyclic graph representing predator-prey relations by drawing an edge [math]\displaystyle{ u-v }[/math] in the competition graph whenever there exists a prey species [math]\displaystyle{ w }[/math] such that the predator-prey relation graph has edges [math]\displaystyle{ u\to w }[/math] and [math]\displaystyle{ v\to w }[/math]. Every competition graph must have at least one isolated vertex, and the competition number of an arbitrary graph represents the smallest number of isolated vertices that could be added to make it into a competition graph. Biologically, if part of a competition graph is observed, then the competition number represents the smallest possible number of unobserved prey species needed to explain it. The competition number is at most equal to the intersection number: one can transform any undirected graph into a competition graph by adding a prey species for each clique in an edge clique cover. However, this relation is not exact, because it is also possible for the predator species to be prey of other species. In a graph with [math]\displaystyle{ n }[/math] vertices, at most [math]\displaystyle{ n-2 }[/math] of them can be the prey of more than one other species, so the competition number is at least the intersection number minus [math]\displaystyle{ n-2 }[/math].[19]

Edge clique covers have also been used to infer the existence of protein complexes, systems of mutually interacting proteins, from protein–protein interaction networks describing only the pairwise interactions between proteins.[20] More generally, Guillaume and Latapy have argued that, for complex networks of all types, replacing the network by a bipartite graph connecting its vertices to the cliques in a clique cover highlights the structure in the network.[21]

Upper bounds

Trivially, a graph with [math]\displaystyle{ m }[/math] edges has intersection number at most [math]\displaystyle{ m }[/math]. Each edge is itself a two-vertex clique. There are [math]\displaystyle{ m }[/math] of these cliques and together they cover all the edges.[22] It is also true that every graph with [math]\displaystyle{ n }[/math] vertices has intersection number at most [math]\displaystyle{ \lfloor n^2/4\rfloor }[/math]. More strongly, the edges of every [math]\displaystyle{ n }[/math]-vertex graph can be covered by at most [math]\displaystyle{ \lfloor n^2/4\rfloor }[/math] cliques, all of which are either single edges or triangles. An algorithm for finding this cover is simple: remove any two adjacent vertices and inductively cover the remaining graph. Restoring the two removed vertices, cover edges to their shared neighbors by triangles, leaving edges to unshared neighbors as two-vertex cliques. The inductive cover has at most [math]\displaystyle{ \lfloor (n-2)^2/4\rfloor }[/math] cliques, and the two removed vertices contribute at most [math]\displaystyle{ n-1 }[/math] cliques, maximized when all other vertices are unshared neighbors and the edge between the two vertices must be used as a clique. Adding these two quantities gives [math]\displaystyle{ \lfloor n^2/4\rfloor }[/math] cliques total.[2][12] This generalizes Mantel's theorem that a triangle-free graph has at most [math]\displaystyle{ \lfloor n^2/4\rfloor }[/math] edges, for in a triangle-free graph the only optimal clique edge cover has one clique per edge and therefore the intersection number equals the number of edges.[2]

An even tighter bound is possible when the number of edges is strictly greater than [math]\displaystyle{ \tfrac{n^2}{4} }[/math]. Let [math]\displaystyle{ p }[/math] be the number of pairs of vertices that are not connected by an edge in the given graph [math]\displaystyle{ G }[/math], and let [math]\displaystyle{ t }[/math] be the unique integer for which [math]\displaystyle{ (t-1)t\le p \lt t(t+1) }[/math]. Then the intersection number of [math]\displaystyle{ G }[/math] is at most [math]\displaystyle{ p+t }[/math].[2][23] Graphs that are the complement of a sparse graph have small intersection numbers: the intersection number of any [math]\displaystyle{ n }[/math]-vertex graph [math]\displaystyle{ G }[/math] is at most [math]\displaystyle{ 2e^2(d+1)^2\ln n }[/math], where [math]\displaystyle{ e }[/math] is the base of the natural logarithm and [math]\displaystyle{ d }[/math] is the maximum degree of the complement graph of [math]\displaystyle{ G }[/math].[6]

It follows from deep results on the structure of claw-free graphs that, when a connected [math]\displaystyle{ n }[/math]-vertex claw-free graph has at least three independent vertices, it has intersection number at most [math]\displaystyle{ n }[/math]. It remains an unsolved problem whether this is true of all claw-free graphs without requiring them to have large independent sets.[8] An important subclass of the claw-free graphs are the line graphs, graphs representing edges and touching pairs of edges of some other graph [math]\displaystyle{ G }[/math]. An optimal clique cover of the line graph [math]\displaystyle{ L(G) }[/math] may be formed with one clique for each triangle in [math]\displaystyle{ G }[/math] that has two or three degree-2 vertices, and one clique for each vertex that has degree at least two and is not a degree-two vertex of one of these triangles. The intersection number is the number of cliques of these two types.[7]

In the Erdős–Rényi–Gilbert model of random graphs, in which all graphs on [math]\displaystyle{ n }[/math] labeled vertices are equally likely (or equivalently, each edge is present or absent, independently of other edges, with probability [math]\displaystyle{ \tfrac12 }[/math]) the intersection number of an [math]\displaystyle{ n }[/math]-vertex random graph is with high probability [math]\displaystyle{ \Theta\left(\frac{n^2}{\log^2n}\right), }[/math] smaller by a factor of [math]\displaystyle{ \log^2 n }[/math] than the number of edges. In these graphs, the maximum cliques have (with high probability) only a logarithmic number of vertices, implying that this many of them are needed to cover all edges. The tricker part of the bound is proving that it is possible to find enough logarithmically-sized cliques to cover many edges, allowing the remaining leftover edges to be covered by two-vertex cliques.[24][25]

Much of the early research on intersection numbers involved calculating these numbers on various specific graphs, such as the graphs formed by removing a complete subgraph or a perfect matching from a larger complete graph.[26]

Computational complexity

Testing whether a given graph [math]\displaystyle{ G }[/math] has intersection number at most a given number [math]\displaystyle{ k }[/math] is NP-complete.[10][7][14] Therefore, it is also NP-hard to compute the intersection number of a given graph. In turn, the hardness of the intersection number has been used to prove that it is NP-complete to recognize the squares of split graphs.[27]

The problem of computing the intersection number is, however, fixed-parameter tractable: that is, it can be solved in an amount of time bounded by a polynomial in [math]\displaystyle{ n }[/math] multiplied by a larger but computable function of the intersection number [math]\displaystyle{ k }[/math].[5][28] This may be shown by observing that there are at most [math]\displaystyle{ 2^k }[/math] distinct closed neighborhoods in the graph – two vertices that belong to the same set of cliques have the same neighborhood – and that the graph formed by selecting one vertex per closed neighborhood has the same intersection number as the original graph.[5][29] Therefore, in polynomial time the input can be reduced to a smaller kernel with at most [math]\displaystyle{ 2^k }[/math] vertices and [math]\displaystyle{ O(4^k) }[/math] edges. Applying an exponential time dynamic programming search procedure over subsets of edges of this kernel gives time [math]\displaystyle{ 2^{O(4^k)}+n^{O(1)} }[/math], double exponential in [math]\displaystyle{ k }[/math].[5][28] The double-exponential dependence on [math]\displaystyle{ k }[/math] cannot be reduced to single exponential by a kernelization of polynomial size, unless the polynomial hierarchy collapses,[30] and if the exponential time hypothesis is true then double-exponential dependence is necessary regardless of whether kernelization is used.[28] On graphs of bounded treewidth, dynamic programming on a tree decomposition of the graph can find the intersection number in linear time,[31][20] but simpler algorithms based on finite sets of reduction rules do not work.[31]

The problem cannot be approximated in polynomial time with an approximation ratio better than [math]\displaystyle{ n^c }[/math], for some constant [math]\displaystyle{ c }[/math],[32] and the best approximation ratio is known is better than the trivial [math]\displaystyle{ O(n^2) }[/math] by only a polylogarithmic factor.[5] Researchers in this area have also investigated the computational efficiency of heuristics, without guarantees on the solution quality they produce, and their behavior on real-world networks.[5][33]

More efficient algorithms are known for certain special classes of graphs. The intersection number of an interval graph is always equal to its number of maximal cliques, which may be computed in polynomial time.[34][35] More generally, in chordal graphs, the intersection number may be computed by an algorithm that considers the vertices in an elimination ordering of the graph (an ordering in which each vertex and its later neighbors form a clique) and that, for each vertex [math]\displaystyle{ v }[/math], forms a clique for [math]\displaystyle{ v }[/math] and its later neighbors whenever at least one of the edges incident to [math]\displaystyle{ v }[/math] is not covered by any earlier clique.[35] It is also possible to find the intersection number in linear time in circular-arc graphs.[36] However, although these graphs have only a polynomial number of cliques to choose among for the cover, having few cliques alone is not enough to make the problem easy: there exist families of graphs with polynomially many cliques for which the intersection number remains NP-hard.[9] The intersection number can also be found in polynomial time for graphs whose maximum degree is five, but is NP-hard for graphs of maximum degree six.[37][38] On planar graphs, computing the intersection number exactly remains NP-hard, but it has a polynomial-time approximation scheme based on Baker's technique.[20]

See also

  • Bipartite dimension, the smallest number of bicliques needed to cover all edges of a graph
  • Bound graph, a type of graph characterized by clique edge covers of a special form
  • Clique cover, the NP-hard problem of finding a small number of cliques that cover all vertices of a graph

References

  1. ↑ 1.0 1.1 1.2 Gross, Jonathan L.; Yellen, Jay (2006), Graph Theory and its Applications, CRC Press, p. 440, ISBN 978-1-58488-505-4 
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 "Applications of edge coverings by cliques", Discrete Applied Mathematics 10 (1): 93–109, 1985, doi:10.1016/0166-218X(85)90061-7 
  3. ↑ 3.0 3.1 Shepherd, F.B.; Vetta, A. (November 2004), "Lighting fibers in a dark network", IEEE Journal on Selected Areas in Communications 22 (9): 1583–1588, doi:10.1109/jsac.2004.833850, https://www.math.mcgill.ca/~vetta/Research.dir/fiber.ps 
  4. ↑ 4.0 4.1 4.2 4.3 Michael, T. S.; Quint, Thomas (2006), "Sphericity, cubicity, and edge clique covers of graphs", Discrete Applied Mathematics 154 (8): 1309–1313, doi:10.1016/j.dam.2006.01.004 
  5. ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Gramm, Jens; Guo, Jiong; Hüffner, Falk (2009), "Data reduction and exact algorithms for clique cover", Journal of Experimental Algorithmics 13 (2): 2–15, doi:10.1145/1412228.1412236, http://www.hueffner.de/falk/clique-cover-jea07.pdf 
  6. ↑ 6.0 6.1 "Covering graphs by the minimum number of equivalence relations", Combinatorica 6 (3): 201–206, 1986, doi:10.1007/bf02579381, https://www.math.tau.ac.il/~nogaa/PDFS/Publications/Covering%20graphs%20by%20the%20minimum%20number%20of%20equivalence%20relations.pdf 
  7. ↑ 7.0 7.1 7.2 Orlin, J. (1977), "Contentment in graph theory: covering graphs with cliques", Indagationes Mathematicae 80 (5): 406–424, doi:10.1016/1385-7258(77)90055-5 
  8. ↑ 8.0 8.1 Javadi, Ramin; Hajebi, Sepehr (2019), "Edge clique cover of claw-free graphs", Journal of Graph Theory 90 (3): 311–405, doi:10.1002/jgt.22403 
  9. ↑ 9.0 9.1 9.2 Rosgen, Bill (2007), "Complexity results on graphs with few cliques", Discrete Mathematics & Theoretical Computer Science 9 (1): 127–135, doi:10.46298/dmtcs.387, https://hal.inria.fr/hal-00966509 
  10. ↑ 10.0 10.1 10.2 10.3 Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman, ISBN 0-7167-1045-5 , Problems GT17 (covering by cliques) and GT59 (intersection graph basis)
  11. ↑ "Sur deux propriétés des classes d'ensembles" (in fr), Fundamenta Mathematicae 33: 303–307, 1945, doi:10.4064/fm-33-1-303-307 
  12. ↑ 12.0 12.1 12.2 12.3 "The representation of a graph by set intersections", Canadian Journal of Mathematics 18 (1): 106–112, 1966, doi:10.4153/CJM-1966-014-3, http://www.renyi.hu/~p_erdos/1966-21.pdf 
  13. ↑ Kellerman, E. (1973), "Determination of keyword conflict", IBM Technical Disclosure Bulletin 16 (2): 544–546 , as cited by (Kou Stockmeyer)
  14. ↑ 14.0 14.1 Kou, L. T. (1978), "Covering edges by cliques with regard to keyword conflicts and intersection graphs", Communications of the ACM 21 (2): 135–139, doi:10.1145/359340.359346 
  15. ↑ "Can visibility graphs be represented compactly?", Discrete & Computational Geometry 12 (3): 347–365, 1994, doi:10.1007/BF02574385 
  16. ↑ Rajagopalan, Subramanian; Vachharajani, Manish; Malik, Sharad (2000), "Handling irregular ILP within conventional VLIW schedulers using artificial resource constraints", Proceedings of the 2000 International Conference on Compilers, Architectures and Synthesis for Embedded Systems, CASES 2000, San Jose, California, USA, November 7–18, 2000, Association for Computing Machinery, pp. 157–164, doi:10.1145/354880.354902 
  17. ↑ Piepho, Hans-Peter (2004), "An algorithm for a letter-based representation of all-pairwise comparisons", Journal of Computational and Graphical Statistics 13 (2): 456–466, doi:10.1198/1061860043515 
  18. ↑ Gramm, Jens; Guo, Jiong; Hüffner, Falk; Niedermeier, Rolf; Piepho, Hans-Peter; Schmid, Ramona (2008), "Algorithms for compact letter displays: Comparison and evaluation", Computational Statistics & Data Analysis 52 (2): 725–736, doi:10.1016/j.csda.2006.09.035 
  19. ↑ Opsut, Robert J. (1982), "On the computation of the competition number of a graph", SIAM Journal on Algebraic and Discrete Methods 3 (4): 420–428, doi:10.1137/0603043 
  20. ↑ 20.0 20.1 20.2 Blanchette, Mathieu; Kim, Ethan; Vetta, Adrian (2012), "Clique cover on sparse networks", in Bader, David A., Proceedings of the 14th Meeting on Algorithm Engineering & Experiments, ALENEX 2012, The Westin Miyako, Kyoto, Japan, January 16, 2012, Society for Industrial and Applied Mathematics, pp. 93–102, doi:10.1137/1.9781611972924.10 
  21. ↑ Guillaume, Jean-Loup; Latapy, Matthieu (2004), "Bipartite structure of all complex networks", Information Processing Letters 90 (5): 215–221, doi:10.1016/j.ipl.2004.03.007, https://hal.archives-ouvertes.fr/hal-00016855/file/guillaume04ipl.pdf 
  22. ↑ Balakrishnan, V. K. (1997), Schaum's Outline of Theory and Problems of Graph Theory, McGraw-Hill Professional, p. 40, ISBN 978-0-07-005489-9 
  23. ↑ "On covering of graphs", Proceedings of the Colloquium held at Tihany, Hungary, 1966, Academic Press, 1968, pp. 231–236 ; as cited by (Roberts 1985)
  24. ↑ "Clique coverings of the edges of a random graph", Combinatorica 13 (1): 1–5, 1993, doi:10.1007/BF01202786, https://faculty.math.illinois.edu/~west/pubs/cliqcovrand.pdf 
  25. ↑ "Covering the edges of a random graph by cliques", Combinatorica 15 (4): 489–497, 1995, doi:10.1007/BF01192522 
  26. ↑ Pullman, Norman J. (1983), "Clique coverings of graphs – A survey", in Reynolds, Louis; Casse, Antoine, Combinatorial Mathematics X: Proceedings of the Conference Held in Adelaide, Australia, August 23-27, 1982, Lecture Notes in Mathematics, 1036, Springer, pp. 72–85, doi:10.1007/bfb0071509, ISBN 978-3-540-12708-6 
  27. ↑ Lau, Lap Chi (2004), "Recognizing powers of proper interval, split, and chordal graphs", SIAM Journal on Discrete Mathematics 18 (1): 83–102, doi:10.1137/S0895480103425930 
  28. ↑ 28.0 28.1 28.2 Cygan, Marek; Pilipczuk, Marcin; Pilipczuk, Michał (2016), "Known algorithms for edge clique cover are probably optimal", SIAM Journal on Computing 45 (1): 67–83, doi:10.1137/130947076 
  29. ↑ "A simple lower bound on edge coverings by cliques", Discrete Mathematics 85 (1): 103–104, 1990, doi:10.1016/0012-365X(90)90168-H 
  30. ↑ Cygan, Marek; Kratsch, Stefan; Pilipczuk, Marcin; Pilipczuk, Michal; Wahlström, Magnus (2014), "Clique cover and graph separation: new incompressibility results", ACM Transactions on Computation Theory 6 (2): 6:1–6:19, doi:10.1145/2594439, http://wrap.warwick.ac.uk/66073/1/WRAP_1371795-cs-270115-main.pdf 
  31. ↑ 31.0 31.1 "Reduction algorithms for graphs of small treewidth", Information and Computation 167 (2): 86–119, 2001, doi:10.1006/inco.2000.2958 
  32. ↑ "On the hardness of approximating minimization problems", Journal of the ACM 41 (5): 960–981, 1994, doi:10.1145/185675.306789 
  33. ↑ Conte, Alessio; Grossi, Roberto; Marino, Andrea (2020), "Large-scale clique cover of real-world networks", Information and Computation 270: Article 104464, 15pp, doi:10.1016/j.ic.2019.104464 
  34. ↑ Opsut, R. J. (1981), "On the fleet maintenance, mobile radio frequency, task assignment, and traffic phasing problems", Proceedings of the 4th International Conference on the Theory and Applications of Graphs, Western Michigan University, Kalamazoo, Michigan, May 6-9, 1980, New York: Wiley, pp. 479–492 ; as cited by (Roberts 1985)
  35. ↑ 35.0 35.1 "On the fractional intersection number of a graph", Graphs and Combinatorics 15 (3): 341–351, 1999, doi:10.1007/s003730050068 
  36. ↑ Hsu, Wen Lian; Tsai, Kuo-Hui (1991), "Linear time algorithms on circular-arc graphs", Information Processing Letters 40 (3): 123–129, doi:10.1016/0020-0190(91)90165-E 
  37. ↑ Pullman, Norman J. (1984), "Clique covering of graphs, IV: Algorithms", SIAM Journal on Computing 13 (1): 57–75, doi:10.1137/0213005 
  38. ↑ Hoover, D. N. (1992), "Complexity of graph covering problems for graphs of low degree", Journal of Combinatorial Mathematics and Combinatorial Computing 11: 187–208 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Intersection_number_(graph_theory)&oldid=3430055"