Inverse-chi-squared distribution

Short description: Probability distribution

Inverse-chi-squared

Probability density function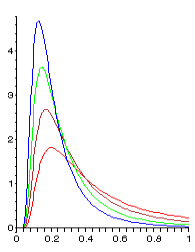
Cumulative distribution function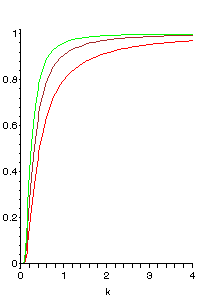
Parameters	$\nu >0$
Support	$x\in (0,\mathrm{\infty })$
PDF	$\frac{2^{-\nu /2}}{\mathrm{\Gamma }(\nu /2)}{x}^{-\nu /2-1}{e}^{-1/(2x)}$
CDF	$\mathrm{\Gamma }(\frac{\nu }{2},\frac{1}{2x})/\mathrm{\Gamma }\left(\frac{\nu }{2}\right)$
Mean	$\frac{1}{\nu -2}$ for $\nu >2$
Median	$\approx \frac{1}{\nu (1-\frac{2}{9\nu }{)}^3}$
Mode	$\frac{1}{\nu +2}$
Variance	$\frac{2}{(\nu -2{)}^2(\nu -4)}$ for $\nu >4$
Skewness	$\frac{4}{\nu -6}\sqrt{2(\nu -4)}$ for $\nu >6$
Kurtosis	$\frac{12(5\nu -22)}{(\nu -6)(\nu -8)}$ for $\nu >8$
Entropy	$\frac{\nu }{2}+\ln \left(\frac{\nu }{2}\mathrm{\Gamma }\left(\frac{\nu }{2}\right)\right)$ $-(1+\frac{\nu }{2})\psi \left(\frac{\nu }{2}\right)$
MGF	$\frac{2}{\mathrm{\Gamma }(\frac{\nu }{2})}{\left(\frac{-t}{2i}\right)}^{\frac{\nu }{4}}{K}_{\frac{\nu }{2}}\left(\sqrt{-2t}\right)$; does not exist as real valued function
CF	$\frac{2}{\mathrm{\Gamma }(\frac{\nu }{2})}{\left(\frac{-it}{2}\right)}^{\frac{\nu }{4}}{K}_{\frac{\nu }{2}}\left(\sqrt{-2it}\right)$

In probability and statistics, the inverse-chi-squared distribution (or inverted-chi-square distribution) is a continuous probability distribution of a positive-valued random variable. It is closely related to the chi-squared distribution. It is used in Bayesian inference as conjugate prior for the variance of the normal distribution.

Definition

The inverse chi-squared distribution (or inverted-chi-square distribution ) is the probability distribution of a random variable whose multiplicative inverse (reciprocal) has a chi-squared distribution.

If $X$ follows a chi-squared distribution with $\nu$ degrees of freedom then $1/X$ follows the inverse chi-squared distribution with $\nu$ degrees of freedom.

The probability density function of the inverse chi-squared distribution is given by

$f(x;\nu )=\frac{2^{-\nu /2}}{\mathrm{\Gamma }(\nu /2)}{x}^{-\nu /2-1}{e}^{-1/(2x)}$

In the above $x>0$ and $\nu$ is the degrees of freedom parameter. Further, $\mathrm{\Gamma }$ is the gamma function.

The inverse chi-squared distribution is a special case of the inverse-gamma distribution. with shape parameter $\alpha =\frac{\nu }{2}$ and scale parameter $\beta =\frac{1}{2}$.

Related distributions

• chi-squared: If $X\sim {\chi }^2(\nu )$ and $Y=\frac{1}{X}$, then $Y\sim \text{Inv-}{\chi }^2(\nu )$
• scaled-inverse chi-squared: If $X\sim \text{Scale-inv-}{\chi }^2(\nu ,1/\nu )$, then $X\sim \text{inv-}{\chi }^2(\nu )$
• Inverse gamma with $\alpha =\frac{\nu }{2}$ and $\beta =\frac{1}{2}$
• Inverse chi-squared distribution is a special case of type 5 Pearson distribution

See also

• Scaled-inverse-chi-squared distribution
• Inverse-Wishart distribution

External links

• InvChisquare in geoR package for the R Language.