Josephus problem

Short description: Mathematical counting-out question

Claude Gaspar Bachet de Méziriac's interpretation of the Josephus problem with 41 soldiers and a step size of 3, showing that places 16 and 31 are last to be killed – time progresses inwards along the spiral, green dots denoting live soldiers, grey dead soldiers, and crosses killings

In computer science and mathematics, the Josephus problem (or Josephus permutation) is a theoretical problem related to a certain counting-out game. Such games are used to pick out a person from a group, e.g. eeny, meeny, miny, moe.

A drawing for the Josephus problem sequence for 500 people and skipping value of 6. The horizontal axis is the number of the person. The vertical axis (top to bottom) is time (the number of cycle). A live person is drawn as green, a dead one is drawn as black.

In the particular counting-out game that gives rise to the Josephus problem, a number of people are standing in a circle waiting to be executed. Counting begins at a specified point in the circle and proceeds around the circle in a specified direction. After a specified number of people are skipped, the next person is executed. The procedure is repeated with the remaining people, starting with the next person, going in the same direction and skipping the same number of people, until only one person remains, and is freed.

The problem—given the number of people, starting point, direction, and number to be skipped—is to choose the position in the initial circle to avoid execution.

History

The problem is named after Flavius Josephus, a Jewish historian living in the 1st century. According to Josephus' firsthand account of the siege of Yodfat, he and his 40 soldiers were trapped in a cave by Roman soldiers. They chose suicide over capture, and settled on a serial method of committing suicide by drawing lots. Josephus states that by luck or possibly by the hand of God, he and another man remained until the end and surrendered to the Romans rather than killing themselves. This is the story given in Book 3, Chapter 8, part 7 of Josephus' The Jewish War (writing of himself in the third person):

However, in this extreme distress, he was not destitute of his usual sagacity; but trusting himself to the providence of God, he put his life into hazard [in the manner following]: "And now," said he, "since it is resolved among you that you will die, come on, let us commit our mutual deaths to determination by lot. He whom the lot falls to first, let him be killed by him that hath the second lot, and thus fortune shall make its progress through us all; nor shall any of us perish by his own right hand, for it would be unfair if, when the rest are gone, somebody should repent and save himself." This proposal appeared to them to be very just; and when he had prevailed with them to determine this matter by lots, he drew one of the lots for himself also. He who had the first lot laid his neck bare to him that had the next, as supposing that the general would die among them immediately; for they thought death, if Josephus might but die with them, was sweeter than life; yet was he with another left to the last, whether we must say it happened so by chance, or whether by the providence of God. And as he was very desirous neither to be condemned by the lot, nor, if he had been left to the last, to imbrue his right hand in the blood of his countrymen, he persuaded him to trust his fidelity to him, and to live as well as himself.

The details of the mechanism used in this feat are rather vague. According to James Dowdy and Michael Mays, in 1612 Claude Gaspard Bachet de Méziriac suggested the specific mechanism of arranging the men in a circle and counting by threes to determine the order of elimination. This story has been often repeated and the specific details vary considerably from source to source. For instance, Israel Nathan Herstein and Irving Kaplansky (1974) have Josephus and 39 comrades stand in a circle with every seventh man eliminated. A history of the problem can be found in S. L. Zabell's Letter to the editor of the Fibonacci Quarterly.

As to intentionality, Josephus asked: “shall we put it down to divine providence or just to luck?” But the surviving Slavonic manuscript of Josephus tells a different story: that he “counted the numbers cunningly and so managed to deceive all the others”. Josephus had an accomplice; the problem was then to find the places of the two last remaining survivors (whose conspiracy would ensure their survival). It is alleged that he placed himself and the other man in the 31st and 16th place respectively (for k = 3 below).

Variants and generalizations

Variant of the Josephus problem with 15 Christians and 15 Turks and a step size of 9 – time progresses inwards along the spiral, green dots denoting live soldiers, grey dead soldiers, and crosses killings

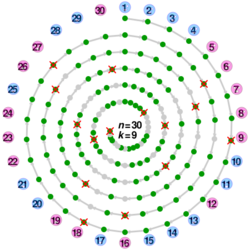
A medieval version of the Josephus problem involves 15 Turks and 15 Christians aboard a ship in a storm which will sink unless half the passengers are thrown overboard. All 30 stand in a circle and every ninth person is to be tossed into the sea. The Christians need to determine where to stand to ensure that only the Turks are tossed. In other versions the roles of Turks and Christians are interchanged.

Graham, Knuth & Patashnik 1989, p. 8 describe and study a "standard" variant: Determine where the last survivor stands if there are n people to start and every second person (k = 2 below) is eliminated.

A generalization of this problem is as follows. It is supposed that every mth person will be executed from a group of size n, in which the pth person is the survivor. If there is an addition of x people to the circle, then the survivor is in the p + mx-th position if this is less than or equal to n + x. If x is the smallest value for which p + mx > n + x, then the survivor is in position (p + mx) − (n + x).

Solution

Penultimate (pink) and ultimate (ultramarine) places in the Josephus problem for various group size, n and step size, k. In the SVG file, hover over the values to show the full order of killing.

In the following, [math]\displaystyle{ n }[/math] denotes the number of people in the initial circle, and [math]\displaystyle{ k }[/math] denotes the count for each step, that is, [math]\displaystyle{ k-1 }[/math] people are skipped and the [math]\displaystyle{ k }[/math]-th is executed. The people in the circle are numbered from [math]\displaystyle{ 1 }[/math] to [math]\displaystyle{ n }[/math], the starting position being [math]\displaystyle{ 1 }[/math] and the counting being inclusive.

k = 2

The problem is explicitly solved when every second person will be killed (every person kills the person on their left or right), i.e. [math]\displaystyle{ k=2 }[/math]. (For the more general case [math]\displaystyle{ k\neq 2 }[/math], a solution is outlined below.) The solution is expressed recursively. Let [math]\displaystyle{ f(n) }[/math] denote the position of the survivor when there are initially n people (and [math]\displaystyle{ k=2 }[/math]). The first time around the circle, all of the even-numbered people die. The second time around the circle, the new 2nd person dies, then the new 4th person, etc.; it is as though there were no first time around the circle.

If the initial number of people was even, then the person in position x during the second time around the circle was originally in position [math]\displaystyle{ 2x - 1 }[/math] (for every choice of x). Let [math]\displaystyle{ n=2j }[/math]. The person at [math]\displaystyle{ f(j) }[/math] who will now survive was originally in position [math]\displaystyle{ 2f(j) - 1 }[/math]. This yields the recurrence

[math]\displaystyle{ f(2j) = 2f(j)-1\;. }[/math]

If the initial number of people was odd, then person 1 can be thought of as dying at the end of the first time around the circle. Again, during the second time around the circle, the new 2nd person dies, then the new 4th person, etc. In this case, the person in position x was originally in position [math]\displaystyle{ 2x+1 }[/math]. This yields the recurrence

[math]\displaystyle{ f(2j+1) = 2f(j)+1\;. }[/math]

When the values are tabulated of [math]\displaystyle{ n }[/math] and [math]\displaystyle{ f(n) }[/math] a pattern emerges (OEIS: A006257, also the leftmost column of blue numbers in the figure above):

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
[math]\displaystyle{ f(n) }[/math]	1	1	3	1	3	5	7	1	3	5	7	9	11	13	15	1

This suggests that [math]\displaystyle{ f(n) }[/math] is an increasing odd sequence that restarts with [math]\displaystyle{ f(n)=1 }[/math] whenever the index n is a power of 2. Therefore, if m and l are chosen so that [math]\displaystyle{ n = 2^m+l }[/math] and [math]\displaystyle{ 0 \leq l \lt 2^m }[/math], then [math]\displaystyle{ f(n) = 2l + 1 }[/math]. It is clear that values in the table satisfy this equation. Or it can be thought that after l people are dead there are only [math]\displaystyle{ 2^m }[/math] people and it goes to the [math]\displaystyle{ 2l+1 }[/math]st person. This person must be the survivor. So [math]\displaystyle{ f(n) = 2l+1 }[/math]. Below, a proof is given by induction.

Theorem: If [math]\displaystyle{ n = 2^m+l }[/math] and [math]\displaystyle{ 0 \leq l \lt 2^m }[/math], then [math]\displaystyle{ f(n) = 2l+1 }[/math].

Proof: The strong induction is used on n. The base case [math]\displaystyle{ n=1 }[/math] is true. The cases are considered separately when n is even and when n is odd.

If n is even, then choose [math]\displaystyle{ l_1 }[/math] and [math]\displaystyle{ m_1 }[/math] such that [math]\displaystyle{ n/2 = 2^{m_1}+l_1 }[/math] and [math]\displaystyle{ 0\leq l_1 \lt 2^{m_1} }[/math]. Note that [math]\displaystyle{ l_1 = l/2 }[/math]. [math]\displaystyle{ f(n) = 2f(n/2)-1=2((2l_1)+1) - 1=2l+1 }[/math] is had where the second equality follows from the induction hypothesis.

If n is odd, then choose [math]\displaystyle{ l_1 }[/math] and [math]\displaystyle{ m_1 }[/math] such that [math]\displaystyle{ (n-1)/2 = 2^{m_1}+l_1 }[/math] and [math]\displaystyle{ 0\leq l_1 \lt 2^{m_1} }[/math]. Note that [math]\displaystyle{ l_1 = (l-1)/2 }[/math]. [math]\displaystyle{ f(n) = 2f((n-1)/2)+1=2((2l_1)+1) + 1=2l+1 }[/math] is had where the second equality follows from the induction hypothesis. This completes the proof.

l can be solved to get an explicit expression for [math]\displaystyle{ f(n) }[/math]:

[math]\displaystyle{ f(n) = 2(n-2^{\lfloor \log_2(n) \rfloor})+1 }[/math]

The most elegant form of the answer involves the binary representation of size n: [math]\displaystyle{ f(n) }[/math] can be obtained by a one-bit left cyclic shift of n itself. If n is represented in binary as [math]\displaystyle{ n = 1 b_1 b_2 b_3\dots b_m }[/math], then the solution is given by [math]\displaystyle{ f(n)=b_1 b_2 b_3 \dots b_m 1 }[/math]. The proof of this follows from the representation of n as [math]\displaystyle{ 2^m+l }[/math] or from the above expression for [math]\displaystyle{ f(n) }[/math].

Implementation: If n denotes the number of people, the safe position is given by the function [math]\displaystyle{ f(n) = 2l+1 }[/math], where [math]\displaystyle{ n=2^m+l }[/math] and [math]\displaystyle{ 0\leq l\lt 2^m }[/math].

Now if the number is represented in binary format, the first bit denotes [math]\displaystyle{ 2^m }[/math] and remaining bits will denote l. For example, when [math]\displaystyle{ n=41 }[/math], its binary representation is:

n    = 1   0   1   0   0   1
2m   = 1   0   0   0   0   0
l    =     0   1   0   0   1

/**
 * @param n the number of people standing in the circle
 * @return the safe position who will survive the execution 
 *   f(N) = 2L + 1 where N =2^M + L and 0 <= L < 2^M
 */
public int getSafePosition(int n) {
	// find value of L for the equation
	int valueOfL = n - Integer.highestOneBit(n);
	return 2 * valueOfL  + 1;
}

Bitwise

The easiest way to find the safe position is by using bitwise operators. In this approach, shifting the most-significant set bit of n to the least significant bit will return the safe position. Input must be a positive integer.

n    = 1   0   1   0   0   1
n    = 0   1   0   0   1   1

/**
 * @param n (41) the number of people standing in the circle
 * @return the safe position who will survive the execution 
 */
public int getSafePosition(int n) {
    return ~Integer.highestOneBit(n*2) & ((n<<1) | 1);
    //     ---------------------- ---  | ------------
    //     Get the first set bit   |   | Left Shift n and flipping the last bit
    //    and take its complement  |   |
    //                             |   |
    //                Multiply n by 2  |
    //                         Bitwise And to copy bits exists in both operands.
}

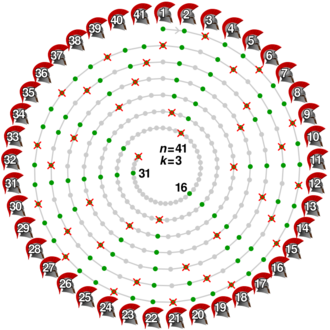
k = 3

In 1997, Lorenz Halbeisen and Norbert Hungerbühler discovered a closed-form for the case [math]\displaystyle{ k=3 }[/math]. They showed that there is a certain constant

[math]\displaystyle{ \alpha \approx 0.8111... }[/math]

that can be computed to arbitrary precision. Given this constant, choose m to be the greatest integer such that [math]\displaystyle{ \operatorname{round}(\alpha \cdot (3/2)^m) \le n }[/math] (this will be either [math]\displaystyle{ m^\prime = \operatorname{round}(\log_{3/2} n/\alpha) }[/math] or [math]\displaystyle{ m^\prime - 1 }[/math]). Then, the final survivor is

[math]\displaystyle{ f(n) = 3(n - \operatorname{round}(\alpha \cdot (3/2)^m)) + (2 }[/math] if is rounded up else [math]\displaystyle{ 1) }[/math]

for all [math]\displaystyle{ n \ge 5 }[/math].

As an example computation, Halbeisen and Hungerbühler give [math]\displaystyle{ n = 41, k = 3 }[/math] (which is actually the original formulation of Josephus' problem). They compute:

[math]\displaystyle{ m^\prime \approx \operatorname{round}(\log_{3/2} 41/0.8111) \approx \operatorname{round}(9.68) = 10 }[/math]

[math]\displaystyle{ \operatorname{round}(\alpha \cdot (3/2)^{m^\prime}) \approx \operatorname{round}(0.8111 \cdot (3/2)^{10}) = 47 }[/math] and therefore [math]\displaystyle{ m = 9 }[/math]

[math]\displaystyle{ \operatorname{round}(0.8111 \cdot (3/2)^9) \approx \operatorname{round}(31.18) = 31 }[/math] (note that this has been rounded down)

[math]\displaystyle{ f(n) = 3(41 - 31) + 1 = 31 }[/math]

This can be verified by looking at each successive pass on the numbers 1 through 41:

1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23, 25, 26, 28, 29, 31, 32, 34, 35, 37, 38, 40, 41

2, 4, 7, 8, 11, 13, 16, 17, 20, 22, 25, 26, 29, 31, 34, 35, 38, 40

2, 4, 8, 11, 16, 17, 22, 25, 29, 31, 35, 38

2, 4, 11, 16, 22, 25, 31, 35

2, 4, 16, 22, 31, 35

4, 16, 31, 35

16, 31

31

The general case

Dynamic programming is used to solve this problem in the general case by performing the first step and then using the solution of the remaining problem. When the index starts from one, then the person at [math]\displaystyle{ s }[/math] shifts from the first person is in position [math]\displaystyle{ ((s-1)\bmod n)+1 }[/math], where n is the total number of people. Let [math]\displaystyle{ f(n,k) }[/math] denote the position of the survivor. After the [math]\displaystyle{ k }[/math]-th person is killed, a circle of [math]\displaystyle{ n-1 }[/math] remains, and the next count is started with the person whose number in the original problem was [math]\displaystyle{ (k\bmod n)+1 }[/math]. The position of the survivor in the remaining circle would be [math]\displaystyle{ f(n-1,k) }[/math] if counting is started at [math]\displaystyle{ 1 }[/math]; shifting this to account for the fact that the starting point is [math]\displaystyle{ (k\bmod n)+1 }[/math] yields the recurrence

[math]\displaystyle{ f(n,k) = ((f(n-1,k)+k-1) \bmod n)+1,\text{ with }f(1,k)=1\,, }[/math]

which takes the simpler form

[math]\displaystyle{ g(n,k) = (g(n-1,k)+k) \bmod n,\text{ with }g(1,k)=0 }[/math]

if the positions are numbered from [math]\displaystyle{ 0 }[/math] to [math]\displaystyle{ n-1 }[/math] instead.

This approach has running time [math]\displaystyle{ O(n) }[/math], but for small [math]\displaystyle{ k }[/math] and large [math]\displaystyle{ n }[/math] there is another approach. The second approach also uses dynamic programming but has running time [math]\displaystyle{ O(k\log n) }[/math]. It is based on considering killing k-th, 2k-th, ..., [math]\displaystyle{ (\lfloor n/k \rfloor k) }[/math]-th people as one step, then changing the numbering.

This improved approach takes the form

[math]\displaystyle{ g(n,k) = \begin{cases} 0 & \text{if } n=1\\ (g(n-1,k)+k) \bmod n & \text{if } 1 \lt n \lt k\\ \begin{Bmatrix} g(n- \left \lfloor \frac{n}{k} \right \rfloor,k)-n \bmod k + n & \text{if } g(n- \left \lfloor \frac{n}{k} \right \rfloor,k)\lt n \bmod k \\ \lfloor \frac{k(g(n- \left \lfloor \frac{n}{k} \right \rfloor,k)-n \bmod k) }{k-1} \rfloor & \text{if } g(n- \left \lfloor \frac{n}{k} \right \rfloor,k) \ge n \bmod k \end{Bmatrix} & \text{if } k \le n\\ \end{cases} }[/math]

References

Sources

• Bachet, C. G. (1612) (in fr). Problemes Plaisants ed Delectables qui se font par les Nombres. 
• Graham, R. L.; Knuth, D. E.; Patashnik, O. (1989). Concrete Mathematics: A Foundation for Computer Science. Addison Wesley. ISBN 978-0-201-14236-5. 
• Herstein, I. N.; Kaplansky, I. (1974). Matters Mathematical. Harper and Row. ISBN 9780060428037. https://archive.org/details/mattersmathemati00hers/page/121. 
• Josephus, Flavius (n.d.). The works of Flavius Josephus : in three volumes ; with illustrations. London: George Routledge & Sons. https://archive.org/details/worksofflaviusjo1873jose/page/578/mode/2up. 
• Newman, J. R. (1988). The World of Mathematics. 4. Tempus. 
• Park, Jang-Woo; Teixeira, Ricardo (2018). "Serial execution Josephus Problem". Korean J. Math 26 (1): 1–7. doi:10.11568/kjm.2018.26.1.1. 
• Robinson, W. J. (1960). "The Josephus problem". Math. Gaz. 44 (347): 47–52. doi:10.2307/3608532. 
• Rouse Ball, W. W. (1905). Mathematical Recreations and Essays (2nd ed.). London: Macmillan. https://www.gutenberg.org/ebooks/26839. 
• Zabell, S. L. (1976). "Letter to the editor". Fibonacci Quarterly 14: 48–51. https://www.fq.math.ca/Issues/14-1.pdf. 

Further reading

• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Chapter 14: Augmenting Data Structures". Introduction to Algorithms (Second ed.). MIT Press and McGraw-Hill. p. 318. ISBN 0-262-03293-7. 
• Dowdy, James; Mays, Michael E. (1989). "Josephus Permutations". Journal of Combinatorial Mathematics and Combinatorial Computing 6: 125–130. https://www.researchgate.net/publication/266756060. 
• Halbeisen, L.; Hungerbühler, N. (1997). "The Josephus Problem". J. Théor. Nombres Bordeaux 9 (2): 303–318. doi:10.5802/jtnb.204. http://www.numdam.org/item/JTNB_1997__9_2_303_0. 
• Jakóbczyk, F. (1973). "On the generalized Josephus problem". Glasow Math. J. 14 (2): 168–173. doi:10.1017/S0017089500001919. 
• Lloyd, Errol L. (1983). "An O(n logm) algorithm for the Josephus Problem". J. Algor. 4 (3): 262–270. doi:10.1016/0196-6774(83)90025-1. 
• Odlyzko, Andrew M.; Wilf, Herbert S. (1991). "Functional iteration and the Josephus problem". Glasgow Math. J. 33 (2): 235–240. doi:10.1017/S0017089500008272. 
• Ruskey, Frank; Williams, Aaron (2010). "The Feline Josephus Problem". Lect. Not. Comp. Sci.. Lecture Notes in Computer Science 6099: 343–354. doi:10.1007/978-3-642-13122-6_33. ISBN 978-3-642-13121-9. Bibcode: 2010LNCS.6099..343R.  FUN2010
• Ruskey, Frank; Williams, Aaron (2012). "The Feline Josephus Problem". Theory Comput. Syst. 50: 20–34. doi:10.1007/s00224-011-9343-6. 
• Sullivan, Shaun; Insko, Erik (2018). "A variant on the Feline Josephus Problem". arXiv:1803.11340 [math.CO].
• Theriault, Nicolas (2001). "Generilazations of the Josephus Problem". Util. Math. (58): 161–173. 
• Woodhouse, David (1973). "The extended Josephus problem". Rev. Mat. Hisp.-Amer. 33 (4): 207–218. 

External links

• Josephus Flavius game (Java Applet) at cut-the-knot allowing selection of every n^th out of 50 (maximum).
• Weisstein, Eric W.. "Josephus Problem". http://mathworld.wolfram.com/JosephusProblem.html. 
• Generalized Josephus Problem