Kirchhoff's diffraction formula

Kirchhoff's diffraction formula (also called Fresnel–Kirchhoff diffraction formula) approximates light intensity and phase in optical diffraction: light fields in the boundary regions of shadows. The approximation can be used to model light propagation in a wide range of configurations, either analytically or using numerical modelling. It gives an expression for the wave disturbance when a monochromatic spherical wave is the incoming wave of a situation under consideration. This formula is derived by applying the Kirchhoff integral theorem, which uses the Green's second identity to derive the solution to the homogeneous scalar wave equation, to a spherical wave with some approximations.

The Huygens–Fresnel principle is derived by the Fresnel–Kirchhoff diffraction formula.

Derivation of Kirchhoff's diffraction formula

Kirchhoff's integral theorem, sometimes referred to as the Fresnel–Kirchhoff integral theorem, uses Green's second identity to derive the solution of the homogeneous scalar wave equation at an arbitrary spatial position P in terms of the solution of the wave equation and its first order derivative at all points on an arbitrary closed surface [math]\displaystyle{ S }[/math] as the boundary of some volume including P.

The solution provided by the integral theorem for a monochromatic source is [math]\displaystyle{ U(\textbf{P}) = \frac{1}{4\pi} \int_{S} \left[ U \frac{\partial}{\partial \textbf{n}} \left( \frac{e^{iks}}{s} \right) - \frac{e^{iks}}{s} \frac{\partial U}{\partial \textbf{n}} \right]dS, }[/math] where [math]\displaystyle{ U }[/math] is the spatial part of the solution of the homogeneous scalar wave equation (i.e., [math]\displaystyle{ V(\mathbf{r},t) = U(\mathbf{r}) e^{-i\omega t} }[/math] as the homogeneous scalar wave equation solution), k is the wavenumber, and s is the distance from P to an (infinitesimally small) integral surface element, and [math]\displaystyle{ \frac{\partial}{\partial n} }[/math] denotes differentiation along the integral surface element normal unit vector [math]\displaystyle{ n }[/math] (i.e., a normal derivative), i.e., [math]\displaystyle{ \frac{\partial f}{\partial n} = \nabla f \cdot n }[/math]. Note that the surface normal or the direction of [math]\displaystyle{ n }[/math] is toward the inside of the enclosed volume in this integral; if the more usual outer-pointing normal is used, the integral will have the opposite sign. And also note that, in the integral theorem shown here, [math]\displaystyle{ n }[/math] and P are vector quantities while other terms are scalar quantities.

For the below cases, the following basic assumptions are made.

• The distance between a point source of waves and an integral area, the distance between the integral area and an observation point P, and the dimension of opening S are much greater than the wave wavelength [math]\displaystyle{ \lambda }[/math].
• [math]\displaystyle{ U }[/math] and [math]\displaystyle{ \frac{\partial U}{\partial n} = \nabla U \cdot n }[/math] are discontinuous at the boundaries of the aperture, called Kirchhoff's boundary conditions. This may be related with another assumption that waves on an aperture (or an open area) is same to the waves that would be present if there was no obstacle for the waves.

Point source

A geometrical arrangement used in deriving the Kirchhoff's diffraction formula. The area designated by A₁ is the aperture (opening), the areas marked by A₂ are opaque areas, and A₃ is the hemisphere as a part of the closed integral surface (consisted of the areas A₁, A₂, and A₃) for the Kirchhoff's integral theorem.

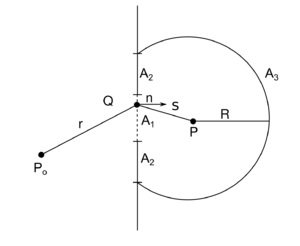
Consider a monochromatic point source at P₀, which illuminates an aperture in a screen. The intensity of the wave emitted by a point source falls off as the inverse square of the distance traveled, so the amplitude falls off as the inverse of the distance. The complex amplitude of the disturbance at a distance [math]\displaystyle{ r }[/math] is given by

[math]\displaystyle{ U(r) = \frac{a e^{ikr}}{r}, }[/math] where [math]\displaystyle{ a }[/math] represents the magnitude of the disturbance at the point source.

The disturbance at a spatial position P can be found by applying the Kirchhoff's integral theorem to the closed surface formed by the intersection of a sphere of radius R with the screen. The integration is performed over the areas A₁, A₂ and A₃, giving [math]\displaystyle{ U(P) = \frac{1}{4\pi} \left[\int_{A_1} + \int_{A_2} + \int_{A_3} \right]\left( U \frac{\partial}{\partial n} \left( \frac{e^{iks}}{s} \right) - \frac{e^{iks}}{s} \frac{\partial U}{\partial n} \right) dS. }[/math]

To solve the equation, it is assumed that the values of [math]\displaystyle{ U }[/math] and [math]\displaystyle{ \frac{\partial U}{\partial n} }[/math] in the aperture area A₁ are the same as when the screen is not present, so at the position Q, [math]\displaystyle{ U_{A_1} = \frac{a e^{ikr}}{r}, }[/math] [math]\displaystyle{ \frac{\partial U_{A_1}}{\partial n} = \nabla U_{A_1} \cdot n = \frac{ae^{ikr}}{r} \left[ik - \frac{1}{r} \right] \cos(n,r), }[/math] where [math]\displaystyle{ r }[/math] is the length of the straight line P₀Q, and [math]\displaystyle{ (n,r) }[/math] is the angle between a straightly extended version of P₀Q and the (inward) normal to the aperture. Note that [math]\displaystyle{ 0 \lt (n,r) \lt \frac{\pi}{2} }[/math] so [math]\displaystyle{ \cos(n,r) }[/math] is a positive real number on A₁.

At Q, we also have [math]\displaystyle{ \frac{\partial}{\partial n} \left( \frac{e^{iks}}{s} \right) = \frac{e^{iks}}{s} \left[ik - \frac{1}{s} \right] \cos(n,s), }[/math] where [math]\displaystyle{ s }[/math] is the length of the straight line PQ, and [math]\displaystyle{ (n,s) }[/math] is the angle between a straightly extended version of PQ and the (inward) normal to the aperture. Note that [math]\displaystyle{ \frac{\pi}{2} \lt (n,s) \lt \frac{3 \pi}{2} }[/math] so [math]\displaystyle{ \cos(n,s) }[/math] is a negative real number on A₁.

Two more following assumptions are made.

• In the above normal derivatives, the terms [math]\displaystyle{ \frac{1}{r} }[/math] and [math]\displaystyle{ \frac{1}{s} }[/math] in the both square brackets are assumed to be negligible compared with the wavenumber [math]\displaystyle{ k=\frac{2\pi}{\lambda} }[/math], means [math]\displaystyle{ r }[/math] and [math]\displaystyle{ s }[/math] are much greater than the wavelength [math]\displaystyle{ \lambda }[/math].
• Kirchhoff assumes that the values of [math]\displaystyle{ U }[/math] and [math]\displaystyle{ \frac{\partial U}{\partial n} }[/math] on the opaque areas marked by A₂ are zero. This implies that [math]\displaystyle{ U }[/math] and [math]\displaystyle{ \frac{\partial U}{\partial n} }[/math] are discontinuous at the edge of the aperture A₁. This is not the case, and this is one of the approximations used in deriving the Kirchhoff's diffraction formula. These assumptions are sometimes referred to as Kirchhoff's boundary conditions.

The contribution from the hemisphere A₃ to the integral is expected to be zero, and it can be justified by one of the following reasons.

1. Make the assumption that the source starts to radiate at a particular time, and then make R large enough, so that when the disturbance at P is being considered, no contributions from A₃ will have arrived there. Such a wave is no longer monochromatic, since a monochromatic wave must exist at all times, but that assumption is not necessary, and a more formal argument avoiding its use has been derived.
2. A wave emanated from the aperture A₁ is expected to evolve toward a spherical wave as it propagates (Water wave examples of this can be found in many pictures showing a water wave passing through a relatively narrow opening.). So, if R is large enough, then the integral on A₃ becomes [math]\displaystyle{ U(P) \sim -\frac{ia}{2\lambda} \int_{A_3} \frac{e^{2ik(r')}}{r'^2} [\cos(n,r') - \cos(n,r')] d{A_3} = -\frac{ia}{2\lambda} \int_{A_3} e^{2ik(r')} [\cos(n,r') - \cos(n,r')] d{\Omega} = 0 }[/math] where [math]\displaystyle{ r' }[/math] and [math]\displaystyle{ d\Omega }[/math] are the distance from the center of the aperture A₁ to an integral surface element and the differential solid angle in the spherical coordinate system respectively.

As a result, finally, the integral above, which represents the complex amplitude at P, becomes [math]\displaystyle{ U(P) = -\frac{ia}{2\lambda} \int_{A_1} \frac{e^{ik(r+s)}}{rs} [\cos(n,r) - \cos(n,s)] d{A_1}. }[/math]

This is the Kirchhoff or Fresnel–Kirchhoff diffraction formula.

Equivalence to Huygens–Fresnel principle

Geometric arrangement used to express Kirchhoff's formula in a form similar to Huygens–Fresnel

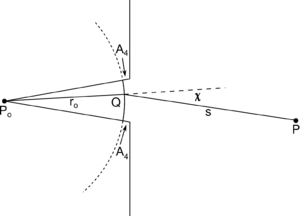
The Huygens–Fresnel principle can be derived by integrating over a different closed surface (the boundary of some volume having an observation point P). The area A₁ above is replaced by a part of a wavefront (emitted from a P₀) at r₀, which is the closest to the aperture, and a portion of a cone with a vertex at P₀, which is labeled A₄ in the right diagram. If the wavefront is positioned such that the wavefront is very close to the edges of the aperture, then the contribution from A₄ can be neglected (assumed here). On this new A₁, the inward (toward the volume enclosed by the closed integral surface, so toward the right side in the diagram) normal [math]\displaystyle{ n }[/math] to A₁ is along the radial direction from P₀, i.e., the direction perpendicular to the wavefront. As a result, the angle [math]\displaystyle{ (n,r)=0 }[/math] and the angle [math]\displaystyle{ (n,s) }[/math] is related with the angle [math]\displaystyle{ \chi }[/math] (the angle as defined in Huygens–Fresnel principle) as [math]\displaystyle{ (n,s) = \pi - \chi. }[/math]

The complex amplitude of the wavefront at r₀ is given by [math]\displaystyle{ U(r_0) = \frac{ae^{ikr_0}}{r_0}. }[/math]

So, the diffraction formula becomes [math]\displaystyle{ U(P) = -\frac{i}{2\lambda} \frac{ae^{ikr_0}}{r_0} \int_{S} \frac{e^{iks}}{s} (1 + \cos\chi) dS, }[/math] where the integral is done over the part of the wavefront at r₀ which is the closest to the aperture in the diagram. This integral leads to the Huygens–Fresnel principle (with the obliquity factor [math]\displaystyle{ \frac {1 + \cos\chi}{2} }[/math]).

In the derivation of this integral, instead of the geometry depicted in the right diagram, double spheres centered at P₀ with the inner sphere radius r₀ and an infinite outer sphere radius can be used. In this geometry, the observation point P is located in the volume enclosed by the two spheres so the Fresnel-Kirchhoff diffraction formula is applied on the two spheres. (The surface normal on these integral surfaces are, say again, toward the enclosed volume in the diffraction formula above.) In the formula application, the integral on the outer sphere is zero by a similar reason of the integral on the hemisphere as zero above.

Extended source

Assume that the aperture is illuminated by an extended source wave. The complex amplitude at the aperture is given by U₀(r).

It is assumed, as before, that the values of [math]\displaystyle{ U }[/math] and [math]\displaystyle{ \frac{\partial U}{\partial n} }[/math] in the area A₁ are the same as when the screen is not present, that the values of [math]\displaystyle{ U }[/math] and [math]\displaystyle{ \frac{\partial U}{\partial n} }[/math] in A₂ are zero (Kirchhoff's boundary conditions) and that the contribution from A₃ to the integral are also zero. It is also assumed that 1/s is negligible compared with k. We then have [math]\displaystyle{ U(P) = \frac{1}{4\pi} \int_{A_1} \frac{e^{iks}}{s} \left[ ik U_0(r) \cos(n,s) - \frac{\partial U_0(r)}{\partial n} \right]\, dS. }[/math]

This is the most general form of the Kirchhoff diffraction formula. To solve this equation for an extended source, an additional integration would be required to sum the contributions made by the individual points in the source. If, however, we assume that the light from the source at each point in the aperture has a well-defined direction, which is the case if the distance between the source and the aperture is significantly greater than the wavelength, then we can write [math]\displaystyle{ U_0(r) \approx a(r) e^{ikr}, }[/math] where a(r) is the magnitude of the disturbance at the point r in the aperture. We then have [math]\displaystyle{ \frac{\partial {U_0(r)}}{\partial n} = ik a(r) \cos(n,r) }[/math] and thus [math]\displaystyle{ U(P) = -\frac{i}{2\lambda} \int_S a(r) \frac{e^{iks}}{s} [ \cos\chi + \cos(n,r)]\, dS. }[/math]

Fraunhofer and Fresnel diffraction equations

In spite of the various approximations that were made in arriving at the formula, it is adequate to describe the majority of problems in instrumental optics. This is mainly because the wavelength of light is much smaller than the dimensions of any obstacles encountered. Analytical solutions are not possible for most configurations, but the Fresnel diffraction equation and Fraunhofer diffraction equation, which are approximations of Kirchhoff's formula for the near field and far field, can be applied to a very wide range of optical systems.

One of the important assumptions made in arriving at the Kirchhoff diffraction formula is that r and s are significantly greater than λ. Another approximation can be made, which significantly simplifies the equation further: this is that the distances P₀Q and QP are much greater than the dimensions of the aperture. This allows one to make two further approximations:

• cos(n, r) − cos(n, s) is replaced with 2cos β, where β is the angle between P₀P and the normal to the aperture. The factor 1/rs is replaced with 1/r's', where r' and s' are the distances from P₀ and P to the origin, which is located in the aperture. The complex amplitude then becomes:[math]\displaystyle{ U(P) = -\frac{ia \cos\beta}{\lambda r's'} \int_S e^{ik(r+s)}\,ds. }[/math]
• Assume that the aperture lies in the xy plane, and the coordinates of P₀, P and Q (a general point in the aperture) are (x₀, y₀, z₀), (x, y, z) and (x', y', 0) respectively. We then have:

  [math]\displaystyle{ ~r^2 = (x_0 - x')^2 + (y_0 - y')^2 + z_0^2, }[/math]

  [math]\displaystyle{ ~s^2 = (x - x')^2 + (y - y')^2 + z^2, }[/math]

  [math]\displaystyle{ ~r'^2 = x_0^2 + y_0^2 + z_0^2, }[/math]

  [math]\displaystyle{ ~s'^2 = x^2 + y^2 + z^2. }[/math]

We can express r and s as follows: [math]\displaystyle{ r = r'\left[1 - \frac{2(x_0x' + y_0y')}{r'^2} + \frac{x'^2 + y'^2}{r'^2}\right]^{1/2}, }[/math] [math]\displaystyle{ s = s'\left[1 - \frac{2(xx' + yy')}{s'^2} + \frac{x'^2 + y'^2}{s'^2}\right]^{1/2}. }[/math]

These can be expanded as power series: [math]\displaystyle{ r = r'\left[1 - \frac{1}{2r'^2}\left[2(x_0x' + y_0y') - (x'^2 + y'^2)\right] + \frac{1}{8r'^4}\left[2(x_0x' + y_0y') - (x'^2 + y'^2)\right]^2 + \cdots\right], }[/math] [math]\displaystyle{ s = s'\left[1 - \frac{1}{2s'^2}\left[2(xx' + yy') - (x'^2 + y'^2)\right] + \frac{1}{8s'^4}\left[2(xx' + yy') - (x'^2 + y'^2)\right]^2 + \cdots\right]. }[/math]

The complex amplitude at P can now be expressed as [math]\displaystyle{ U(P) = -\frac{i\cos\beta}{\lambda} \frac{ae^{ik(r' + s')}}{r's'} \int_S e^{ikf(x',y')}\, dx' dy', }[/math] where f(x', y') includes all the terms in the expressions above for s and r apart from the first term in each expression and can be written in the form [math]\displaystyle{ f(x',y') = c_1 x' + c_2 y' + c_3 x'^2 + c_4 y'^2 + c_5x'y' \cdots, }[/math] where the c_i are constants.

Fraunhofer diffraction

If all the terms in f(x', y') can be neglected except for the terms in x' and y', we have the Fraunhofer diffraction equation. If the direction cosines of P₀Q and PQ are [math]\displaystyle{ \begin{align} l_0 &= -x_0/r', \\ m_0 &= -y_0/r', \\ l &= x/s', \\ m &= y/s'. \end{align} }[/math]

The Fraunhofer diffraction equation is then [math]\displaystyle{ U(P) = C \int_S e^{ik[(l_0 - l)x' + (m_0 - m)y']}\, dx' dy', }[/math] where C is a constant. This can also be written in the form [math]\displaystyle{ U(P) = C\int_S e^{i(\mathbf k_0 - \mathbf k) \cdot \mathbf r'}\, dr', }[/math] where k₀ and k are the wave vectors of the waves traveling from P₀ to the aperture and from the aperture to P respectively, and r' is a point in the aperture.

If the point source is replaced by an extended source whose complex amplitude at the aperture is given by U₀(r' ), then the Fraunhofer diffraction equation is: [math]\displaystyle{ U(P) \propto \int_S a_0 (\mathbf r') e^{i(\mathbf k_0 - \mathbf k) \cdot \mathbf r'}\, dr', }[/math] where a₀(r') is, as before, the magnitude of the disturbance at the aperture.

In addition to the approximations made in deriving the Kirchhoff equation, it is assumed that

• r and s are significantly greater than the size of the aperture,
• second- and higher-order terms in the expression f(x', y') can be neglected.

Fresnel diffraction

When the quadratic terms cannot be neglected but all higher order terms can, the equation becomes the Fresnel diffraction equation. The approximations for the Kirchhoff equation are used, and additional assumptions are:

• r and s are significantly greater than the size of the aperture,
• third- and higher-order terms in the expression f(x', y') can be neglected.

Further reading

• Baker, B.B.; Copson, E.T. (1939, 1950). The Mathematical Theory of Huygens' Principle. Oxford.
• Woan, Graham (2000). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 9780521575072. https://archive.org/details/cambridgehandboo0000woan. 
• J. Goodman (2005). Introduction to Fourier Optics (3rd ed.). Roberts & Co Publishers. ISBN 978-0-9747077-2-3. https://books.google.com/books?id=ow5xs_Rtt9AC. 
• Griffiths, David J. (2012). Introduction to Electrodynamics. Pearson Education, Limited. ISBN 978-0-321-85656-2. https://books.google.com/books?id=t-Q6LgEACAAJ. 
• Band, Yehuda B. (2006). Light and Matter: Electromagnetism, Optics, Spectroscopy and Lasers. John Wiley & Sons. ISBN 978-0-471-89931-0. https://books.google.com/books?id=0Rar9yGfQfgC. 
• Kenyon, Ian (2008). The Light Fantastic: A Modern Introduction to Classical and Quantum Optics. Oxford University Press. ISBN 978-0-19-856646-5. https://archive.org/details/lightfantasticmo0000keny. 
• Lerner, Rita G.; George L., Trigg (1991). Encyclopedia of physics. VCH. ISBN 978-0-89573-752-6. https://archive.org/details/encyclopediaofph00lern. 
• Sybil P., Parker (1993). MacGraw-Hill Encyclopedia of Physics. McGraw-Hill Ryerson, Limited. ISBN 978-0-07-051400-3. https://books.google.com/books?id=q-H4MQEACAAJ.