Kobon triangle problem

Kobon triangles generated with 3, 4 and 5 straight line segments.

Unsolved problem in mathematics: How many non-overlapping triangles can be formed in an arrangement of [math]\displaystyle{ k }[/math] lines? (more unsolved problems in mathematics)

The Kobon triangle problem is an unsolved problem in combinatorial geometry first stated by Kobon Fujimura (1903-1983). The problem asks for the largest number N(k) of nonoverlapping triangles whose sides lie on an arrangement of k lines. Variations of the problem consider the projective plane rather than the Euclidean plane, and require that the triangles not be crossed by any other lines of the arrangement.

Known upper bounds

Saburo Tamura proved that the number of nonoverlapping triangles realizable by [math]\displaystyle{ k }[/math] lines is at most [math]\displaystyle{ \lfloor k(k-2)/3\rfloor }[/math]. G. Clément and J. Bader proved more strongly that this bound cannot be achieved when [math]\displaystyle{ k }[/math] is congruent to 0 or 2 (mod 6). The maximum number of triangles is therefore at most one less in these cases. The same bounds can be equivalently stated, without use of the floor function, as: [math]\displaystyle{ \begin{cases} \frac 13 k (k-2) & \text{when } k \equiv 3,5 \pmod{6}; \\ \frac 13 (k+1)(k-3) & \text{when } k \equiv 0,2 \pmod{6}; \\ \frac 13 (k^2-2k-2) & \text{when } k \equiv 1,4 \pmod{6}. \end{cases} }[/math]

Solutions yielding this number of triangles are known when [math]\displaystyle{ k }[/math] is 3, 4, 5, 6, 7, 8, 9, 13, 15 or 17. For k = 10, 11 and 12, the best solutions known reach a number of triangles one less than the upper bound.

Known constructions

Given an optimal solution with k₀ > 3 lines, other Kobon triangle solution numbers can be found for all k_i-values where [math]\displaystyle{ k_{n+1} = 2\cdot k_{n} - 1, }[/math] by using the procedure by D. Forge and J. L. Ramirez Alfonsin. For example, the solution for k₀ = 5 leads to the maximal number of nonoverlapping triangles for k = 5, 9, 17, 33, 65, ....

k	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	OEIS
Tamura's upper bound on N(k)	1	2	5	8	11	16	21	26	33	40	47	56	65	74	85	96	107	120	133	A032765
Clément and Bader's upper bound	1	2	5	7	11	15	21	26	33	39	47	55	65	74	85	95	107	119	133	-
best known solution	1	2	5	7	11	15	21	25	32	38	47	53	65	72	85	93	104	115	130	A006066

Examples

• 

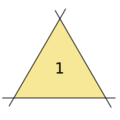
  3 lines, 1 triangle

• 

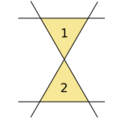
  4 lines, 2 triangles

• 

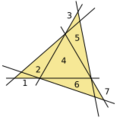
  5 lines, 5 triangles

• 

  6 lines, 7 triangles

• 

  7 lines, 11 triangles

See also

• Roberts's triangle theorem, on the minimum number of triangles that [math]\displaystyle{ n }[/math] lines can form

External links

• Johannes Bader, "Kobon Triangles"