Roberts's triangle theorem

Short description: On triangles in line arrangements

Seven lines tangent to a semicircle form five triangular faces

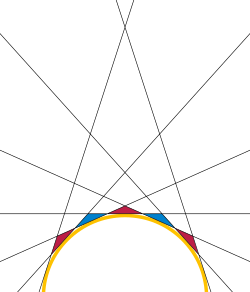
Roberts's triangle theorem, a result in discrete geometry, states that every simple arrangement of [math]\displaystyle{ n }[/math] lines has at least [math]\displaystyle{ n-2 }[/math] triangular faces. Thus, three lines form a triangle, four lines form at least two triangles, five lines form at least three triangles, etc. It is named after Samuel Roberts, a British mathematician who published it in 1889.

Statement and example

The theorem states that every simple arrangement of [math]\displaystyle{ n }[/math] lines in the Euclidean plane has at least [math]\displaystyle{ n-2 }[/math] triangular faces. Here, an arrangement is simple when it has no two parallel lines and no three lines through the same point. A face is one of the polygons formed by the arrangement, but not crossed by any of its lines. Faces may be bounded or infinite, but only the bounded faces with exactly three sides count as triangles for the purposes of the theorem.

One way to form an arrangement of [math]\displaystyle{ n }[/math] lines with exactly [math]\displaystyle{ n-2 }[/math] triangular faces is to choose the lines to be tangent to a semicircle. For lines arranged in this way, the only triangles are the ones formed by three lines with consecutive points of tangency. The other faces of this arrangement are either bounded quadrilaterals, or unbounded. As the [math]\displaystyle{ n }[/math] lines have [math]\displaystyle{ n-2 }[/math] consecutive triples, they also have [math]\displaystyle{ n-2 }[/math] triangles.

Proof

Branko Grünbaum found the proof in Roberts's original paper "unconvincing", and credits the first correct proof of Roberts's theorem to Robert W. Shannon, in 1979. He presents instead the following more elementary argument, first published in Russian by Alexei Belov. It depends implicitly on a simpler version of the same theorem, according to which every simple arrangement of three or more lines has at least one triangular face. This follows easily by induction from the fact that adding a line to an arrangement cannot decrease the number of triangular faces: if the line cuts an existing triangle, one of the resulting two pieces is again a triangle. If it were true more strongly that adding a line always increased the number of triangles, then a similar induction would prove Roberts's theorem, but it is not true. There exist arrangements for which, after adding a line, the number of triangles remains unchanged.

Instead, Belov uses the following argument. If the [math]\displaystyle{ n }[/math] given lines are all moved without changing their slopes, their new positions can be described by a system of [math]\displaystyle{ n }[/math] real numbers, the offsets of each line from its original position. For each triangular face, there is a linear equation on the offsets of its three lines that, if satisfied, causes the face to retain its original area. If there could be fewer than [math]\displaystyle{ n-2 }[/math] triangles, then (because there would be more variables than equations constraining them) it would be possible to fix two of the lines in place and find a simultaneous linear motion of all remaining lines, keeping their slopes fixed, that preserves all of the triangle areas. Such a motion must pass through arrangements that are not simple, for instance when one of the moving lines passes over the crossing point of the two fixed lines. At the time when the moving lines first form a non-simple arrangement, three or more lines meet at a point. Just before these lines meet, this subset of lines would have a triangular face (also present in the original arrangement) whose area approaches zero. But this contradicts the invariance of the face areas. The contradiction shows that the assumption that there are fewer than [math]\displaystyle{ n-2 }[/math] triangles cannot be true.

Related results

Five triangles solve the Kobon triangle problem for five lines

Whereas Roberts's theorem concerns the fewest possible triangles made by a given number of lines, the related Kobon triangle problem concerns the largest number possible. The two problems differ already for [math]\displaystyle{ n=5 }[/math], where Roberts's theorem guarantees that three triangles will exist, but the solution to the Kobon triangle problem has five triangles.

Roberts's theorem can be generalized from simple line arrangements to some non-simple arrangements, to arrangements in the projective plane rather than in the Euclidean plane, and to arrangements of hyperplanes in higher-dimensional spaces. Beyond line arrangements, the same bound as Roberts's theorem holds for arrangements of pseudolines.