Lewis's triviality result

In the mathematical theory of probability, David Lewis's triviality result is a theorem about the impossibility of systematically equating the conditional probability [math]\displaystyle{ P(B\mid A) }[/math] with the probability of a so-called conditional event, [math]\displaystyle{ A \rightarrow B }[/math].

Conditional probability and conditional events

The statement "The probability that if [math]\displaystyle{ A }[/math], then [math]\displaystyle{ B }[/math], is 20%" means (put intuitively) that event [math]\displaystyle{ B }[/math] may be expected to occur in 20% of the outcomes where event [math]\displaystyle{ A }[/math] occurs. The standard formal expression of this is [math]\displaystyle{ P(B\mid A)=0.20 }[/math], where the conditional probability [math]\displaystyle{ P(B\mid A) }[/math] equals, by definition, [math]\displaystyle{ P(A \cap B)/P(A) }[/math].

Beginning in the 1960s, several philosophical logicians—most notably Ernest Adams and Robert Stalnaker—floated the idea that one might also write [math]\displaystyle{ P(A \rightarrow B) = 0.20 }[/math], where [math]\displaystyle{ A \rightarrow B }[/math] is the conditional event "If [math]\displaystyle{ A }[/math], then [math]\displaystyle{ B }[/math]". That is, given events [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], one might suppose there is an event, [math]\displaystyle{ A \rightarrow B }[/math], such that [math]\displaystyle{ P(A \rightarrow B) }[/math] could be counted on to equal [math]\displaystyle{ P(B\mid A) }[/math], so long as [math]\displaystyle{ P(A) \gt 0 }[/math].

Part of the appeal of this move would be the possibility of embedding conditional expressions within more complex constructions. One could write, say, [math]\displaystyle{ P(A \cup (B \rightarrow C)) = 0.75 }[/math], to express someone's high subjective degree of confidence ("75% sure") that either [math]\displaystyle{ A }[/math], or else if [math]\displaystyle{ B }[/math], then [math]\displaystyle{ C }[/math]. Compound constructions containing conditional expressions might also be useful in the programming of automated decision-making systems.

Fig. 1 – A diagram of [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ A \rightarrow B }[/math]. The [math]\displaystyle{ \rightarrow }[/math] symbol is not assumed to represent any particular operation. Specifically, it is not assumed that [math]\displaystyle{ A \rightarrow B }[/math] can be identified with [math]\displaystyle{ A' \cup B }[/math].

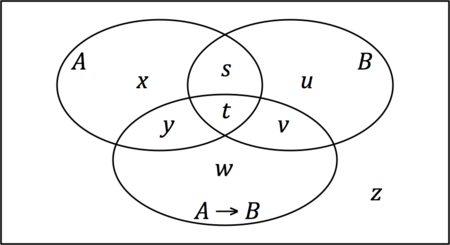
How might such a convention be combined with standard probability theory? The most direct extension of the standard theory would be to treat [math]\displaystyle{ A \rightarrow B }[/math] as an event like any other, i.e., as a set of outcomes. Adding [math]\displaystyle{ A \rightarrow B }[/math] to the familiar Venn- or Euler diagram of [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] would then result in something like Fig. 1, where [math]\displaystyle{ s,t,\ldots, z }[/math] are probabilities allocated to the eight respective regions, such that [math]\displaystyle{ s + t + \cdots + z = 1 }[/math].

For [math]\displaystyle{ P(A \rightarrow B) }[/math] to equal [math]\displaystyle{ P(B\mid A) }[/math] requires that [math]\displaystyle{ t + v + w + y = (s + t)/(s + t + x + y) }[/math], i.e., that the probability inside the [math]\displaystyle{ A \rightarrow B }[/math] region equal the [math]\displaystyle{ A \cap B }[/math] region's proportional share of the probability inside the [math]\displaystyle{ A }[/math] region. In general the equality will of course not be true, so that making it reliably true requires a new constraint on probability functions: in addition to satisfying Kolmogorov's probability axioms, they must also satisfy a new constraint, namely that [math]\displaystyle{ P(A \rightarrow B) = P(B\mid A) }[/math] for any events [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] such that [math]\displaystyle{ P(A) \gt 0 }[/math].

Lewis's result

(Lewis 1976) pointed out a seemingly fatal problem with the above proposal: assuming a nontrivial set of events, the new, restricted class of [math]\displaystyle{ P }[/math]-functions will not be closed under conditioning, the operation that turns probability function [math]\displaystyle{ P }[/math] into new function [math]\displaystyle{ P_C (\cdot) = P(\cdot\mid C) }[/math], predicated on event [math]\displaystyle{ C }[/math]'s occurrence. That is, if [math]\displaystyle{ P(A \rightarrow B) = P(B\mid A) }[/math], it will not in general be true that [math]\displaystyle{ P_C(A \rightarrow B) = P_C(B\mid A) }[/math] as long as [math]\displaystyle{ P(C)\gt 0 }[/math]. This implies that if rationality requires having a well-behaved probability function, then a fully rational person (or computing system) would become irrational simply in virtue of learning that arbitrary event [math]\displaystyle{ C }[/math] had occurred. Bas van Fraassen called this result "a veritable bombshell" (van Fraassen|1976}}|1976, p. 273).

Lewis's proof is as follows. Let a set of events be non-trivial if it contains two possible events, [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], that are mutually exclusive but do not together exhaust all possibilities, so that [math]\displaystyle{ P(A) \gt 0 }[/math], [math]\displaystyle{ P(B) \gt 0 }[/math], [math]\displaystyle{ P(A \cap B) = 0 }[/math], and [math]\displaystyle{ P(A \cup B) \lt 1 }[/math]. The existence of two such events implies the existence of the event [math]\displaystyle{ A \cup B }[/math], as well, and, if conditional events are admitted, the event [math]\displaystyle{ (A \cup B) \rightarrow A }[/math]. The proof derives a contradiction from the assumption that such a minimally non-trivial set of events exists.

1. Consider the probability of [math]\displaystyle{ (A \cup B) \rightarrow A }[/math] after conditioning, first on [math]\displaystyle{ A }[/math] and then instead on [math]\displaystyle{ A' }[/math].
   • Conditioning on [math]\displaystyle{ A }[/math] gives [math]\displaystyle{ P_A((A \cup B) \rightarrow A) = P(((A \cup B) \rightarrow A) \cap A)/P(A) }[/math]. But also, by the new constraint on [math]\displaystyle{ P }[/math]-functions, [math]\displaystyle{ P_A((A \cup B) \rightarrow A) = P_A((A \cup B) \cap A)/P_A(A \cup B) = }[/math] [math]\displaystyle{ P((A \cup B) \cap A\mid A)/P(A \cup B\mid A) = 1/1 = 1 }[/math]. Therefore, [math]\displaystyle{ P(((A \cup B) \rightarrow A) \cap A) = P(A) }[/math].
   • Conditioning on [math]\displaystyle{ A' }[/math] gives [math]\displaystyle{ P_{A'}((A \cup B) \rightarrow A) = P(((A \cup B) \rightarrow A) \cap A')/P(A') }[/math]. But also, [math]\displaystyle{ P_{A'}((A \cup B) \rightarrow A) = P_{A'}((A \cup B) \cap A)/P_{A'}(A \cup B) = }[/math] [math]\displaystyle{ P((A \cup B) \cap A\mid A')/P(A \cup B\mid A') = 0/P(A \cup B\mid A') = 0 }[/math]. (The mutual exclusivity of [math]\displaystyle{ B }[/math] and [math]\displaystyle{ A }[/math] ensures that [math]\displaystyle{ P(A \cup B\mid A') \neq 0 }[/math].) Therefore, [math]\displaystyle{ P(((A \cup B) \rightarrow A) \cap A') = 0 }[/math].
2. Instantiate the identity [math]\displaystyle{ P(X \cap Y) + P(X \cap Y') = P(X) }[/math] as [math]\displaystyle{ P(((A \cup B) \rightarrow A) \cap A) + P(((A \cup B) \rightarrow A) \cap A') = }[/math] [math]\displaystyle{ P((A \cup B) \rightarrow A) }[/math]. By the results from Step 1, the left side reduces to [math]\displaystyle{ P(A) }[/math], while the right side, by the new constraint on [math]\displaystyle{ P }[/math]-functions, equals [math]\displaystyle{ P((A \cup B) \cap A)/P(A \cup B) = P(A)/P(A \cup B) }[/math]. Therefore, [math]\displaystyle{ P(A) = P(A)/P(A \cup B) }[/math], which means that [math]\displaystyle{ P(A \cup B) = 1 }[/math], which contradicts the stipulation that [math]\displaystyle{ P(A \cup B) \lt 1 }[/math]. This completes the proof.

Graphical version

Fig. 2 – A diagram of disjoint [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], and [math]\displaystyle{ (A \cup B) \rightarrow A }[/math].

A graphical version of the proof starts with Fig. 2, where the [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] from Fig. 1 are now disjoint and [math]\displaystyle{ A \rightarrow B }[/math] has been replaced by [math]\displaystyle{ (A \cup B) \rightarrow A }[/math]. By the assumption that [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are possible, [math]\displaystyle{ x+y\gt 0 }[/math] and [math]\displaystyle{ u+v\gt 0 }[/math]. By the assumption that together [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] do not together exhaust all possibilities, [math]\displaystyle{ u + v + x + y \lt 1 }[/math]. And by the new constraint on probability functions, [math]\displaystyle{ P((A \cup B) \rightarrow A) = P(A\mid A \cup B) = }[/math] [math]\displaystyle{ P(A \cap (A \cup B))/P(A \cup B) = P(A)/P(A \cup B) }[/math], which means that

(1) [math]\displaystyle{ y + v + w =\frac{x + y}{x + y + u + v}, }[/math]

Conditioning on an event involves zeroing out the probabilities outside the event's region and increasing the probabilities inside the region by a common scale factor. Here, conditioning on [math]\displaystyle{ A }[/math] will zero out [math]\displaystyle{ u, v }[/math] and [math]\displaystyle{ w }[/math] and scale up [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math], to [math]\displaystyle{ x_A }[/math] and [math]\displaystyle{ y_A }[/math], respectively, and so

(2) [math]\displaystyle{ y_A + 0 + 0 = \frac{x_A + y_A}{x_A + y_A + 0 + 0}, }[/math] which simplifies to [math]\displaystyle{ y_A = 1. }[/math]

Conditioning instead on [math]\displaystyle{ A' }[/math] will zero out [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] and scale up [math]\displaystyle{ u, v }[/math] and [math]\displaystyle{ w }[/math], and so

(3) [math]\displaystyle{ 0 + v_{A'} + w_{A'} = \frac{0 + 0}{0 + 0 + u_A + v_A}, }[/math] which simplifies to [math]\displaystyle{ v_{A'} + w_{A'} = 0. }[/math]

From (2), it follows that [math]\displaystyle{ x_A = 0 }[/math], and since [math]\displaystyle{ x_A }[/math] is the scaled-up value of [math]\displaystyle{ x }[/math], it must also be that [math]\displaystyle{ x = 0 }[/math]. Similarly, from (3), [math]\displaystyle{ v = w = 0 }[/math]. But then (1) reduces to [math]\displaystyle{ y = y/(y + u) }[/math], which implies that [math]\displaystyle{ y + u = 1 }[/math], which contradicts the stipulation that [math]\displaystyle{ u + v + x + y \lt 1 }[/math].

Later developments

In a follow-up article, (Lewis 1986) noted that the triviality proof can proceed by conditioning not on [math]\displaystyle{ A }[/math] and [math]\displaystyle{ A' }[/math] but instead, by turns, on each of a finite set of mutually exclusive and jointly exhaustive events [math]\displaystyle{ A, C, D, E, \ldots\,. }[/math] He also gave a variant of the proof that involved not total conditioning, in which the probability of either [math]\displaystyle{ A }[/math] or [math]\displaystyle{ A' }[/math] is set to 1, but partial conditioning (i.e., Jeffrey conditioning), by which probability is incrementally shifted from [math]\displaystyle{ A' }[/math] to [math]\displaystyle{ A }[/math].

Separately, (Hájek 1989) pointed out that even without conditioning, if the number of outcomes is large but finite, then in general [math]\displaystyle{ P(B\mid A) = P(A \cap B)/P(A) }[/math], being a ratio of two outputs of the [math]\displaystyle{ P }[/math]-function, will take on more values than any single output of the function can. So, for instance, if in Fig. 1 [math]\displaystyle{ s, t, \ldots }[/math] are all multiples of 0.01 (as would be the case if there were exactly 100 equiprobable outcomes), then [math]\displaystyle{ P(A \rightarrow B) }[/math] must be a multiple of 0.01, as well, but [math]\displaystyle{ P(A \cap B)/P(A) }[/math] need not be. That being the case, [math]\displaystyle{ P(A \rightarrow B) }[/math] cannot reliably be made to equal [math]\displaystyle{ P(B \mid A) }[/math].

(Hájek 1994) also argued that the condition [math]\displaystyle{ P(A \rightarrow B) = P(B\mid A) }[/math] caused acceptable [math]\displaystyle{ P }[/math]-functions to be implausibly sparse and isolated from one another. One way to put the point: standardly, any weighted average of two probability function is itself a probability function, so that between any two [math]\displaystyle{ P }[/math]-functions there will be a continuum of weighted-average [math]\displaystyle{ P }[/math]-functions along which one of the original [math]\displaystyle{ P }[/math]-functions gradually transforms into the other. But these continua disappear if the added [math]\displaystyle{ P(A \rightarrow B) = P(B\mid A) }[/math] condition is imposed. Now an average of two acceptable [math]\displaystyle{ P }[/math]-functions will in general not be an acceptable [math]\displaystyle{ P }[/math]-function.

Possible rejoinders

Assuming that [math]\displaystyle{ P(A \rightarrow B) = P(B\mid A) }[/math] holds for a minimally nontrivial set of events and for any [math]\displaystyle{ P }[/math]-function leads to a contradiction. Thus [math]\displaystyle{ P(A \rightarrow B) = P(B\mid A) }[/math] can hold for any [math]\displaystyle{ P }[/math]-function only for trivial sets of events—that is the triviality result. However, the proof relies on background assumptions that may be challenged. It may be proposed, for instance, that the referent event of an expression like “[math]\displaystyle{ A \rightarrow B }[/math]” is not fixed for a given [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], but instead changes as the probability function changes. Or it may be proposed that conditioning on [math]\displaystyle{ C }[/math] should follow a rule other than [math]\displaystyle{ P_C(\cdot) = P(\cdot\mid C) }[/math].

But the most common response, among proponents of the [math]\displaystyle{ P(A \rightarrow B) = P(B\mid A) }[/math] condition, has been to explore ways to model conditional events as something other than subsets of a universe set of outcomes. Even before Lewis published his result, (Schay 1968) had modeled conditional events as ordered pairs of sets of outcomes. With that approach and others in the same spirit, conditional events and their associated combination and complementation operations do not constitute the usual algebra of sets of standard probability theory, but rather a more exotic type of structure, known as a conditional event algebra.

References

• Hájek, Alan (1989). "Probabilities of conditionals – Revisited". Journal of Philosophical Logic 18 (4): 423–428. doi:10.1007/BF00262944. 
• Hájek, Alan (1994). "Triviality on the cheap?". in Eells, Ellery; Skyrms, Brian. Probability and Conditionals. Cambridge UP. pp. 113–140. ISBN 978-0521039338. 
• Hájek, Alan; Hall, Ned (1994). "The hypothesis of the conditional construal of conditional probability". in Eells, Ellery; Skyrms, Brian. Probability and Conditionals. Cambridge UP. pp. 75–111. ISBN 978-0521039338. 
• Lewis, David (1976). "Probabilities of conditionals and conditional probabilities". Philosophical Review 85 (3): 297–315. doi:10.2307/2184045. 
• Lewis, David (1986). "Probabilities of conditionals and conditional probabilities II". Philosophical Review 95 (4): 581–589. doi:10.2307/2185051. 
• Schay, Geza (1968). "An algebra of conditional events". Journal of Mathematical Analysis and Applications 24 (2): 334–344. doi:10.1016/0022-247X(68)90035-8. 
• van Fraassen, Bas C. (1976). "Probabilities of conditionals". in Harper, W.; Hooker, C.. Foundations and Philosophy of Epistemic Applications of Probability Theory. Foundations of Probability Theory, Statistical Inference, and Statistical Theories of Science, Volume I. D. Reidel. pp. 261–308. ISBN 978-9027706171.