List of irreducible Tits indices

Short description: none

In the mathematical theory of linear algebraic groups, a Tits index (or index) is an object used to classify semisimple algebraic groups defined over a base field k, not assumed to be algebraically closed. The possible irreducible indices were classified by Jacques Tits, and this classification is reproduced below. (Because every index is a direct sum of irreducible indices, classifying all indices amounts to classifying irreducible indices.)

Organization of the list

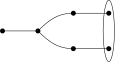
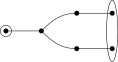
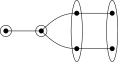
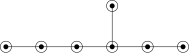
An index can be represented as a Dynkin diagram with certain vertices drawn close to each other (the orbit of the vertices under the *-action of the Galois group of k) and with certain sets of vertices circled (the orbits of the non-distinguished vertices under the *-action). This representation captures the full information of the index except when the underlying Dynkin diagram is D₄, in which case one must distinguish between an action by the cyclic group C₃ or the permutation group S₃.

Alternatively, an index can be represented using the name of the underlying Dykin diagram together with additional superscripts and subscripts, to be explained momentarily. This representation, together with the labeled Dynkin diagram described in the previous paragraph, captures the full information of the index.

The notation for an index is of the form ^gXtn,r, where

• X is the letter of the underlying Dynkin diagram (A, B, C, D, E, F, or G),
• n is the number of vertices of the Dynkin diagram,
• r is the relative rank of the corresponding algebraic group,
• g is the order of the quotient of the absolute Galois group that acts faithfully on the Dynkin diagram (so g = 1, 2, 3, or 6), and
• t is either
  • the degree of a certain division algebra (that is, the square root of its dimension) arising in the construction of the algebraic group when the group is of classical type (A, B, C, or D), in which case t is written in parentheses, or
  • the dimension of the anisotropic kernel of the algebraic group when the group is of exceptional type (E, F, or G), in which case t is written without parentheses.

A_n

¹A_n

Image:

Full name: ¹A(d)n,r

Conditions: d · (r + 1) = n + 1, d ≥ 1.

Algebraic group: The special linear group SL_r+1(D) where D is a central division algebra over k.

Special fields: Over a finite field, d = 1; over the reals, d = 1 or 2; over a p-adic field or a number field, d is arbitrary.

²A_n

Image:

Full name: ²A(d)n,r

Conditions: d | n + 1, d ≥ 1, 2rd ≤ n + 1.

Algebraic group: The special unitary group SU_(n+1)/d(D,h), where D is a central division algebra of degree d over a separable quadratic extension k' of k, and where h is a nondegenerate hermitian form of index r relative to the unique non-trivial k-automorphism of k' .

Special fields: Over a finite field, d = 1 and r = ⌊(n+1)/2⌋; over the reals, d = 1; over a p-adic field, d = 1 and n = 2r − 1; over a number field, d and r are arbitrary.

B_n

Image:

Full name: B_n,r

Conditions: None.

Algebraic group: The special orthogonal group SO_2n+1(k,q), where q is a quadratic form of index r, and defect 1 if k has characteristic 2.

Special fields: Over a finite field, r = n; over a p-adic field, r = n or n − 1; over the reals or a number field, r is arbitrary.

C_n

Image:

Full name: C(d)n,r

Conditions: d = 2^a | 2n, d ≥ 1; n = r if d = 1.

Algebraic group: The special unitary group SU_2n/d(D,h), where D is a division algebra of degree d over k and h is a nondegenerate antihermitian form relative to a k-linear involution σ of D (also called an "involution of the first kind") such that the fixed-point subring D^σ has dimension 1/2 d(d + 1); or equivalently, when d > 1 and char k ≠ 2, the group SU_2n/d where D and h are as above except that h is hermitian and D has dimension 1/2 d(d − 1). When d = 1, this group is the symplectic group Sp_2n(k).

Special fields: Over a finite field, d = 1; over the reals or a number field, d = 1 (and r = n) or d = 2; over a p-adic field, d = 1 (and r = n) or d = 2, and n = 2r or 2r − 1.

D_n

¹D_n

Image:

Full name: ¹D(d)n,r

Conditions: d is a power of 2, d | 2n, d ≥ 1, rd ≤ n, n ≠ rd + 1.

Algebraic group: If k has characteristic 2, the same as for C_n except that h is a hermitian form of discriminant 1 and index r.

Special fields: Over a finite field, d = 1 and n = r; over the reals, d = 1 and n − r = 2m, or d = 2 and n = 2r; over a p-adic field, d = 1 and r = n or n − 2, or d = 2 and n = 2r or 2r + 3; over a number field, d = 1 and n − r = 2m, or d = 2 and n − 2r = 2m or 3.

²D_n

Full name: ²D(d)n,r

Image:

³D284,0

Image:

⁶D284,0

Image:

³D94,1

Image:

⁶D94,1

Image:

³D24,2

Image:

⁶D24,2

Image:

E₆

¹E786,0

Image:

¹E286,2

Image:

¹E166,2

Image:

¹E06,6

Image:

²E786,0

Image:

²E356,1

Image:

²E296,1

Image:

²E16'6,2

Image:

²E16"6,2

Image:

²E26,4

Image:

E₇

E1337,0

Image:

E787,1

Image:

E667,1

Image:

E487,1

Image:

E317,2

Image:

E287,3

Image:

E97,4

Image:

E07,7

Image:

E₈

E2488,0

Image:

E1338,1

Image:

E918,1

Image:

E788,2

Image:

E668,2

Image:

E288,4

Image:

E08,8

Image:

F₄

F524,0

Image:

Algebraic Group: The automorphism group of an exceptional simple Jordan algebra J that does not contain nonzero nilpotent elements.

F214,1

Image:

Algebraic Group: The automorphism group of an exceptional simple Jordan algebra J containing nonzero nilpotent elements, no two of which are nonproportional and orthogonal.

F04,4

Image:

Algebraic Group: The automorphism group of an exceptional simple Jordan algebra J containing nonproportional orthogonal nilpotent elements.

G₂

A group of type G₂ is always the automorphism group of an octonion algebra.

G142,0

Image:

Algebraic group: the automorphism group of a division octonion algebra.

Special fields: Exists over the reals and number fields; does not exist over finite fields or a p-adic field.

G02,2

Image:

Algebraic group: the automorphism group of a split octonion algebra.

Special fields: Exists over a finite field, the reals, a p-adic field, and a number field.

References

• Tits, Jacques (1966), "Classification of algebraic semisimple groups", Algebraic Groups and Discontinuous Subgroups (Proc. Sympos. Pure Math., Boulder, Colo., 1965), Providence, R.I.: American Mathematical Society, pp. 33–62 
• Jacobson, Nathan (1939), "Cayley numbers and simple Lie algebras of type G", Duke Mathematical Journal 5: 775–783, doi:10.1215/s0012-7094-39-00562-4 
• Linear Algebraic Groups (2nd ed.), New York: Birkhäuser, 1998, ISBN 0-8176-4021-5