Log-Laplace distribution
From HandWiki
|
Probability density function  Probability density functions for Log-Laplace distributions with varying parameters [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ b }[/math]. | |||
|
Cumulative distribution function  Cumulative distribution functions for Log-Laplace distributions with varying parameters [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ b }[/math]. |
In probability theory and statistics, the log-Laplace distribution is the probability distribution of a random variable whose logarithm has a Laplace distribution. If X has a Laplace distribution with parameters μ and b, then Y = eX has a log-Laplace distribution. The distributional properties can be derived from the Laplace distribution.
Characterization
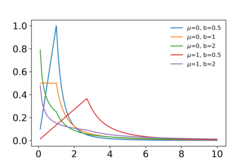
A random variable has a log-Laplace(μ, b) distribution if its probability density function is:[1]
- [math]\displaystyle{ f(x|\mu,b) = \frac{1}{2bx} \exp \left( -\frac{|\ln x-\mu|}{b} \right) }[/math]
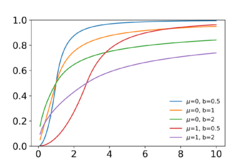
The cumulative distribution function for Y when y > 0, is
- [math]\displaystyle{ F(y) = 0.5\,[1 + \sgn(\ln(y)-\mu)\,(1-\exp(-|\ln(y)-\mu|/b))]. }[/math]
Generalization
Versions of the log-Laplace distribution based on an asymmetric Laplace distribution also exist.[2] Depending on the parameters, including asymmetry, the log-Laplace may or may not have a finite mean and a finite variance.[2]
References
- ↑ Lindsey, J.K. (2004). Statistical analysis of stochastic processes in time. Cambridge University Press. p. 33. ISBN 978-0-521-83741-5.
- ↑ 2.0 2.1 "A Log-Laplace Growth Rate Model". University of Nevada-Reno. p. 4. http://wolfweb.unr.edu/homepage/tkozubow/0_logs.pdf.
External links
 |  |
