Magic square of squares

Short description: Unsolved problem in mathematics

Unsolved problem in {{{1}}}: {{{2}}} (more unsolved problems in {{{1}}})

The magic square of squares is an unsolved problem in mathematics which asks whether it is possible to construct a three-by-three magic square, the elements of which are all square numbers. The problem was first posed anonymously by Martin LaBar in 1984, before being included in Richard Guy's Unsolved problems in number theory (2nd edition) in 1994.

The problem has been a popular choice for recreational mathematicians following two articles Martin Gardner published in Quantum Magazine on the problem, offering a prize of US$100 in 1996. Other prizes have subsequently been offered for the first solution.

Background

Main article: Magic square

The smallest (and unique up to rotation and reflection) non-trivial case of a magic square, order 3

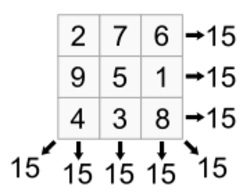
A magic square is a square array of integer numbers in which each row, column and diagonal sums to the same number. The order of the square refers to the number of integers along each side. A trivial magic square is a magic square which has at least one repeated element, and a semimagic square is a magic square in which the rows and columns, but not both diagonals sum to the same number.

Problem

The problem asks whether it is possible to construct a third-order magic square such that every element is itself a square number. A square which solves the problem would thus be of the form

$x_1^2$	$x_2^2$	$x_3^2$
$x_4^2$	$x_5^2$	$x_6^2$
$x_7^2$	$x_8^2$	$x_9^2$

and satisfy the following equations

$\begin{array}{rl}{x}_1^2+x_2^2+x_3^2& =x_4^2+x_5^2+x_6^2\\ & =x_7^2+x_8^2+x_9^2\\ & =x_1^2+x_5^2+x_9^2\\ & =x_3^2+x_5^2+x_7^2\\ & =x_1^2+x_4^2+x_7^2\\ & =x_2^2+x_5^2+x_8^2\\ & =x_3^2+x_6^2+x_9^2\end{array}$

Current research

It has been shown that the problem is equivalent to several other problems.

1. Do there exist three arithmetic progressions such that each has three terms, each has the same difference between terms as the other two, the terms are all perfect squares, and the middle terms of the three arithmetic progressions themselves form an arithmetic progression?
2. Do there exist three rational right triangles with the same area, such that the squares of the hypotenuses are in arithmetic progression?
3. Does there exist an elliptic curve, $y^2=x^3-n^{2}x$, where $n$ is a congruent number, with three rational points on the curve, $(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$, such that each point is "double" another rational point on the curve ("double" in the sense of the group structure for points on an elliptic curve), and $x_1$, $x_2$ and $x_3$ are in arithmetic progression?

Brute force searches for solutions have been unsuccessful, and suggest that if a solution exists, it would consist of numbers greater than at least $10^{14}$.

Rice University professor of mathematics Anthony Várilly-Alvarado has expressed his doubt as to the existence of the magic square of squares.

Notable attempts

There have been a number of attempts to construct a magic square of squares by recreational mathematicians.

Sallows' Square

Following Gardner's prize offer for anyone who could find a magic square of squares in 1996, Lee Sallows published his attempt in The Mathematical Intelligencer. His attempt is unique in that the all of the rows and columns, and one of the diagonals all sum to a square number.

Sallows' Square

	1272	462	582	1472
	22	1132	942	1472
	742	822	972	1472
1472	1472	1472	1472	38307

Bremner Square

In 1999, Andrew Bremner published his attempt at the problem, and further research surrounding magic squares of squares. Bremner's attempt differs from others in that not all elements of the square are square numbers, while all the rows, columns and diagonals sum to the same number.

Bremner Square

	3732	2892	5652	541875
	360721	4252	232	541875
	2052	5272	222121	541875
541875	541875	541875	541875	541875

Parker square

The Parker square is an attempt by Matt Parker to solve the problem. His solution is a trivial, semimagic square of squares, as $41^2$, $29^2$ and $1^2$ all appear twice, and the diagonal $23^2+37^2+47^2$ sums to 4107, instead of 3051.

The Parker Square, with sums shown in bold.

	292	12	472	3051
	412	372	12	3051
	232	412	292	3051
4107	3051	3051	3051	3051

Non third-order magic squares of squares

Magic squares of squares of orders greater than 3 have been known since as early as 1770, when Leonard Euler sent a letter to Joseph-Louis Lagrange detailing a fourth-order magic square.

Euler's magic square of squares

682	292	412	372
172	312	792	322
592	282	232	612
112	772	82	492

Multimagic squares are magic squares which remain magic after raising every element to some power. In 1890, Georges Pfeffermann published a solution to a problem he posed involving the construction of an eighth-order 2-multimagic square.

Pfeffermann's eighth order 2-multimagic square

	56	34	8	57	18	47	9	31	260
	33	20	54	48	7	29	59	10	260
	26	43	13	23	64	38	4	49	260
	19	5	35	30	53	12	46	60	260
	15	25	63	2	41	24	50	40	260
	6	55	17	11	36	58	32	45	260
	61	16	42	52	27	1	39	22	260
	44	62	28	37	14	51	21	3	260
260	260	260	260	260	260	260	260	260	260