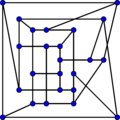
McGee graph

From HandWiki
Short description: Graph with 24 vertices and 36 edges
McGee graph
File:220px
The McGee graph
Named afterW. F. McGee
Vertices24
Edges36
Radius4
Diameter4[1]
Girth7[1]
Automorphisms32[1]
Chromatic number3[1]
Chromatic index3[1]
Book thickness3
Queue number2
PropertiesCubic
Cage
Hamiltonian
Table of graphs and parameters

In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.[1]

The McGee graph is the unique (3,7)-cage (the smallest cubic graph of girth 7). It is also the smallest cubic cage that is not a Moore graph.

First discovered by Sachs but unpublished,[2] the graph is named after McGee who published the result in 1960.[3] Then, the McGee graph was proven the unique (3,7)-cage by Tutte in 1966.[4][5][6]

The McGee graph requires at least eight crossings in any drawing of it in the plane. It is one of three non-isomorphic graphs tied for being the smallest cubic graph that requires eight crossings. Another of these three graphs is the generalized Petersen graph G(12,5), also known as the Nauru graph.[7][8]

The McGee graph has radius 4, diameter 4, chromatic number 3 and chromatic index 3. It is also a 3-vertex-connected and a 3-edge-connected graph. It has book thickness 3 and queue number 2.[9]

Algebraic properties

The characteristic polynomial of the McGee graph is

x3(x−3)(x−2)3(x+1)2(x+2)(x2+x−4)(x3+x2−4x−2)4.

The automorphism group of the McGee graph is of order 32 and doesn't act transitively upon its vertices: there are two vertex orbits, of lengths 8 and 16. The McGee graph is the smallest cubic cage that is not a vertex-transitive graph.[10]

The automorphism group of the McGee graph, meaning its group of symmetries, has 32 elements. This group is isomorphic to the group of all affine transformations of ℤ/8ℤ, i.e., transformations of the form

x↦ax+b

where a,b∈ℤ/8ℤ and a is invertible, so a=1,3,5,7.[11] This is one of the two smallest possible group G with an outer automorphism that maps every element g∈G to an element conjugate to g.[12]

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Weisstein, Eric W.. "McGee Graph". http://mathworld.wolfram.com/McGeeGraph.html. 
  2. ↑ Kárteszi, F. "Piani finit ciclici come risoluzioni di un certo problemo di minimo." Boll. Un. Mat. Ital. 15, 522-528, 1960
  3. ↑ McGee, W. F. (1960). "A Minimal Cubic Graph of Girth Seven". Canadian Mathematical Bulletin 3 (2): 149–152. doi:10.4153/CMB-1960-018-1. 
  4. ↑ Tutte, W. T. Connectivity in Graphs. Toronto, Ontario: University of Toronto Press, 1966
  5. ↑ Wong, Pak-Ken (1982). "Cages—A Survey". Journal of Graph Theory 6: 1–22. doi:10.1002/jgt.3190060103. 
  6. ↑ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance Regular Graphs. New York: Springer-Verlag, p. 209, 1989
  7. ↑ Sloane, N. J. A., ed. "Sequence A110507 (Number of nodes in the smallest cubic graph with crossing number n)". OEIS Foundation. https://oeis.org/A110507. 
  8. ↑ Pegg, E. T.; Exoo, G. (2009). "Crossing number graphs". Mathematica Journal 11 (2). doi:10.3888/tmj.11.2-2. http://www.mathematica-journal.com/issue/v11i2/CrossingNumberGraphs.html. .
  9. ↑ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
  10. ↑ Jajcay, Robert; Širáň, Jozef (2011). "Small vertex-transitive graphs of given degree and girth". Ars Mathematica Contemporanea 4 (2): 375–384. doi:10.26493/1855-3974.124.06d. 
  11. ↑ John C. Baez, What algebraic structures are related to the McGee graph?, https://mathoverflow.net/q/215211
  12. ↑ Peter A. Brooksbank and Matthew S. Mizuhara (2014). On groups with a class-preserving outer automorphism, Involve. Vol. 7, No. 2, 171–179. doi:10.2140/involve.2014.7.171 https://msp.org/involve/2014/7-2/p04.xhtml



Retrieved from "https://handwiki.org/wiki/index.php?title=McGee_graph&oldid=3979128"