Cage (graph theory)

Short description: Regular graph with fewest possible nodes for its girth

The Tutte (3,8)-cage.

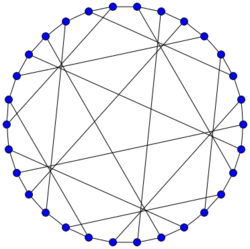
In the mathematical field of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.

Formally, an (r, g)-graph is defined to be a graph in which each vertex has exactly r neighbors, and in which the shortest cycle has length exactly g. An (r, g)-cage is an (r, g)-graph with the smallest possible number of vertices, among all (r, g)-graphs. A (3, g)-cage is often called a g-cage.

It is known that an (r, g)-graph exists for any combination of r ≥ 2 and g ≥ 3. It follows that all (r, g)-cages exist.

If a Moore graph exists with degree r and girth g, it must be a cage. Moreover, the bounds on the sizes of Moore graphs generalize to cages: any cage with odd girth g must have at least

[math]\displaystyle{ 1+r\sum_{i=0}^{(g-3)/2}(r-1)^i }[/math]

vertices, and any cage with even girth g must have at least

[math]\displaystyle{ 2\sum_{i=0}^{(g-2)/2}(r-1)^i }[/math]

vertices. Any (r, g)-graph with exactly this many vertices is by definition a Moore graph and therefore automatically a cage.

There may exist multiple cages for a given combination of r and g. For instance there are three nonisomorphic (3, 10)-cages, each with 70 vertices: the Balaban 10-cage, the Harries graph and the Harries–Wong graph. But there is only one (3, 11)-cage: the Balaban 11-cage (with 112 vertices).

Known cages

A 1-regular graph has no cycle, and a connected 2-regular graph has girth equal to its number of vertices, so cages are only of interest for r ≥ 3. The (r,3)-cage is a complete graph K_r+1 on r+1 vertices, and the (r,4)-cage is a complete bipartite graph K_r,r on 2r vertices.

Notable cages include:

• (3,5)-cage: the Petersen graph, 10 vertices
• (3,6)-cage: the Heawood graph, 14 vertices
• (3,7)-cage: the McGee graph, 24 vertices
• (3,8)-cage: the Tutte–Coxeter graph, 30 vertices
• (3,10)-cage: the Balaban 10-cage, 70 vertices
• (3,11)-cage: the Balaban 11-cage, 112 vertices
• (4,5)-cage: the Robertson graph, 19 vertices
• (7,5)-cage: The Hoffman–Singleton graph, 50 vertices.
• When r − 1 is a prime power, the (r,6) cages are the incidence graphs of projective planes.
• When r − 1 is a prime power, the (r,8) and (r,12) cages are generalized polygons.

The numbers of vertices in the known (r,g) cages, for values of r > 2 and g > 2, other than projective planes and generalized polygons, are:

g r	3	4	5	6	7	8	9	10	11	12
3	4	6	10	14	24	30	58	70	112	126
4	5	8	19	26	67	80				728
5	6	10	30	42		170				2730
6	7	12	40	62		312				7812
7	8	14	50	90

Asymptotics

For large values of g, the Moore bound implies that the number n of vertices must grow at least singly exponentially as a function of g. Equivalently, g can be at most proportional to the logarithm of n. More precisely,

[math]\displaystyle{ g\le 2\log_{r-1} n + O(1). }[/math]

It is believed that this bound is tight or close to tight (Bollobás Szemerédi). The best known lower bounds on g are also logarithmic, but with a smaller constant factor (implying that n grows singly exponentially but at a higher rate than the Moore bound). Specifically, the construction of Ramanujan graphs defined by (Lubotzky Phillips) satisfy the bound

[math]\displaystyle{ g\ge \frac{4}{3}\log_{r-1} n + O(1). }[/math]

This bound was improved slightly by (Lazebnik Ustimenko).

It is unlikely that these graphs are themselves cages, but their existence gives an upper bound to the number of vertices needed in a cage.

References

• Algebraic Graph Theory (2nd ed.), Cambridge Mathematical Library, 1993, pp. 180–190, ISBN 0-521-45897-8 .
• "Girth of sparse graphs", Journal of Graph Theory 39 (3): 194–200, 2002, doi:10.1002/jgt.10023 .
• Exoo, G; Jajcay, R (2008), "Dynamic Cage Survey", Electronic Journal of Combinatorics DS16, http://www.combinatorics.org/ojs/index.php/eljc/article/download/ds16/pdf, retrieved 2012-03-25 .
• Erdős, Paul; Rényi, Alfréd; Sós, Vera T. (1966), "On a problem of graph theory", Studia Sci. Math. Hungar. 1: 215–235, http://www.math-inst.hu/~p_erdos/1966-06.pdf, retrieved 2010-02-23 .
• Hartsfield, Nora; Ringel, Gerhard (1990), Pearls in Graph Theory: A Comprehensive Introduction, Academic Press, pp. 77–81, ISBN 0-12-328552-6 .
• Holton, D. A.; Sheehan, J. (1993), The Petersen Graph, Cambridge University Press, pp. 183–213, ISBN 0-521-43594-3 .
• Lazebnik, F.; Ustimenko, V. A.; Woldar, A. J. (1995), "A new series of dense graphs of high girth", Bulletin of the American Mathematical Society, New Series 32 (1): 73–79, doi:10.1090/S0273-0979-1995-00569-0 .
• "Ramanujan graphs", Combinatorica 8 (3): 261–277, 1988, doi:10.1007/BF02126799 .
• "A family of cubical graphs", Proc. Cambridge Philos. Soc. 43 (4): 459–474, 1947, doi:10.1017/S0305004100023720, Bibcode: 1947PCPS...43..459T .

External links

• Brouwer, Andries E. Cages
• Royle, Gordon. Cubic Cages and Higher valency cages
• Weisstein, Eric W.. "Cage Graph". http://mathworld.wolfram.com/CageGraph.html.