Mean absolute error
In statistics, mean absolute error (MAE) is a measure of errors between paired observations expressing the same phenomenon. Examples of Y versus X include comparisons of predicted versus observed, subsequent time versus initial time, and one technique of measurement versus an alternative technique of measurement. MAE is calculated as the sum of absolute errors divided by the sample size:[1][math]\displaystyle{ \mathrm{MAE} = \frac{\sum_{i=1}^n\left| y_i - x_i\right|}{n} =\frac{\sum_{i=1}^n\left| e_i \right|}{n}. }[/math]It is thus an arithmetic average of the absolute errors [math]\displaystyle{ |e_i| = |y_i - x_i| }[/math], where [math]\displaystyle{ y_i }[/math] is the prediction and [math]\displaystyle{ x_i }[/math] the true value. Alternative formulations may include relative frequencies as weight factors. The mean absolute error uses the same scale as the data being measured. This is known as a scale-dependent accuracy measure and therefore cannot be used to make comparisons between predicted values that use different scales.[2] The mean absolute error is a common measure of forecast error in time series analysis,[3] sometimes used in confusion with the more standard definition of mean absolute deviation. The same confusion exists more generally.
Quantity disagreement and allocation disagreement
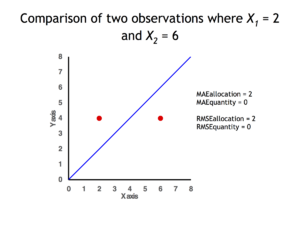
In remote sensing the MAE is sometimes expressed as the sum of two components: quantity disagreement and allocation disagreement. Quantity disagreement is the absolute value of the mean error:[4][math]\displaystyle{ \left|\frac{\sum_{i=1}^n y_i-x_i}{n}\right|. }[/math]Allocation disagreement is MAE minus quantity disagreement.
It is also possible to identify the types of difference by looking at an [math]\displaystyle{ (x,y) }[/math] plot. Quantity difference exists when the average of the X values does not equal the average of the Y values. Allocation difference exists if and only if points reside on both sides of the identity line.[4][5]
Related measures
The mean absolute error is one of a number of ways of comparing forecasts with their eventual outcomes. Well-established alternatives are the mean absolute scaled error (MASE) and the mean squared error. These all summarize performance in ways that disregard the direction of over- or under- prediction; a measure that does place emphasis on this is the mean signed difference.
Where a prediction model is to be fitted using a selected performance measure, in the sense that the least squares approach is related to the mean squared error, the equivalent for mean absolute error is least absolute deviations.
MAE is not identical to root-mean square error (RMSE), although some researchers report and interpret it that way. The MAE is conceptually simpler and also easier to interpret than RMSE: it is simply the average absolute vertical or horizontal distance between each point in a scatter plot and the Y=X line. In other words, MAE is the average absolute difference between X and Y. Furthermore, each error contributes to MAE in proportion to the absolute value of the error. This is in contrast to RMSE which involves squaring the differences, so that a few large differences will increase the RMSE to a greater degree than the MAE.[4]
Optimality property
The mean absolute error of a real variable c with respect to the random variable X is[math]\displaystyle{ E(\left|X-c\right|). }[/math]Provided that the probability distribution of X is such that the above expectation exists, then m is a median of X if and only if m is a minimizer of the mean absolute error with respect to X.[6] In particular, m is a sample median if and only if m minimizes the arithmetic mean of the absolute deviations.[7]
More generally, a median is defined as a minimum of[math]\displaystyle{ E(|X-c| - |X| ), }[/math]as discussed at Multivariate median (and specifically at Spatial median). This optimization-based definition of the median is useful in statistical data-analysis, for example, in k-medians clustering.
Proof of optimality
Statement: The classifier minimising [math]\displaystyle{ \mathbb{E}|y-\hat{y}| }[/math] is [math]\displaystyle{ \hat{f}(x)=\text{Median}(y|X=x) }[/math] .
Proof:
The Loss functions for classification is[math]\displaystyle{ \begin{align} L &= \mathbb{E}[|y-a||X=x]\\ &= \int_{-\infty}^{\infty}|y-a|f_{Y|X}(y)\, dy\\ &= \int_{-\infty}^a (a-y)f_{Y|X}(y)\, dy+\int_a^{\infty}(y-a)f_{Y|X}(y)\, dy.\\ \end{align} }[/math]Differentiating with respect to a gives[math]\displaystyle{ \frac{\partial }{\partial a}L = \int_{-\infty}^af_{Y|X}(y)\, dy+\int_a^{\infty}-f_{Y|X}(y)\, dy=0 . }[/math]This means[math]\displaystyle{ \int_{-\infty}^a f(y)\, dy = \int_a^{\infty} f(y)\, dy . }[/math]Hence,[math]\displaystyle{ F_{Y|X}(a)=0.5 . }[/math]
See also
- Least absolute deviations
- Mean absolute percentage error
- Mean percentage error
- Symmetric mean absolute percentage error
References
- ↑ Willmott, Cort J.; Matsuura, Kenji (December 19, 2005). "Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance". Climate Research 30: 79–82. doi:10.3354/cr030079.
- ↑ "2.5 Evaluating forecast accuracy | OTexts". https://www.otexts.org/fpp/2/5.
- ↑ Hyndman, R. and Koehler A. (2005). "Another look at measures of forecast accuracy" [1]
- ↑ Jump up to: 4.0 4.1 4.2 Pontius Jr., Robert Gilmore; Thontteh, Olufunmilayo; Chen, Hao (2008). "Components of information for multiple resolution comparison between maps that share a real variable". Environmental and Ecological Statistics 15 (2): 111–142. doi:10.1007/s10651-007-0043-y. https://commons.clarku.edu/context/faculty_geography/article/1769/viewcontent/GeogFacWorks_Pontius_Components_2006.pdf.
- ↑ Willmott, C. J.; Matsuura, K. (January 2006). "On the use of dimensioned measures of error to evaluate the performance of spatial interpolators". International Journal of Geographical Information Science 20: 89–102. doi:10.1080/13658810500286976.
- ↑ Stroock, Daniel (2011). Probability Theory. Cambridge University Press. pp. 43. ISBN 978-0-521-13250-3. https://archive.org/details/probabilitytheor00stro.
- ↑ DeGroot, Morris H. (1970). Optimal Statistical Decisions. McGraw-Hill Book Co., New York-London-Sydney. p. 232. ISBN 9780471680291. https://books.google.com/books?id=7rDY2_r4bmEC&pg=PA232.
 |