Mylar balloon (geometry)
In geometry, a mylar balloon is a surface of revolution. While a sphere is the surface that encloses a maximal volume for a given surface area, the mylar balloon instead maximizes volume for a given generatrix arc length. It resembles a slightly flattened sphere.
The shape is approximately realized by inflating a physical balloon made of two circular sheets of flexible, inelastic material; for example, a popular type of toy balloon made of aluminized plastic. Perhaps counterintuitively, the surface area of the inflated balloon is less than the surface area of the circular sheets. This is due to physical crimping of the surface, which increases near the rim.
"Mylar balloon" is the name for the figure given by W. Paulson, who first investigated the shape. The term was subsequently adopted by other writers. "Mylar" is a trademark of DuPont.
Definition
The positive portion of the generatrix of the balloon is the function z(x) where for a given generatrix length a:
- [math]\displaystyle{ z(r)=0 }[/math]
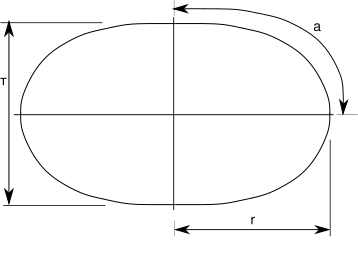
- [math]\displaystyle{ \int_0^r \!\sqrt{1+z'(x)^2}\,dx \, = a }[/math] (i.e.: the generatrix length is given)
- [math]\displaystyle{ \int_0^r \! 4\pi x z(x) \, dx }[/math] is a maximum (i.e.: the volume is maximum)
Here, the radius r is determined from the constraints.
Parametric characterization
The parametric equations for the generatrix of a balloon of radius r are given by:
- [math]\displaystyle{ x(u) = r \cos u;\qquad z(u) = r \sqrt{2} \left[ E(u,\frac{1}{\sqrt{2}})-\frac{1}{2}F(u, \frac{1}{\sqrt{2}})\right]\text{ for }u \in [0, \frac{\pi}{2}] \, }[/math]
(where E and F are elliptic integrals of the second and first kind)
Measurement
The "thickness" of the balloon (that is, the distance across at the axis of rotation) can be determined by calculating [math]\displaystyle{ 2 z({\frac{\pi}{2}} ) }[/math] from the parametric equations above. The thickness τ is given by
- [math]\displaystyle{ {\tau} = 2Br, }[/math]
while the generatrix length a is given by
- [math]\displaystyle{ a = Ar }[/math]
where r is the radius; A ≈ 1.3110287771 and B ≈ 0.5990701173 are the first and second lemniscate constants.
Volume
The volume of the balloon is given by:
- [math]\displaystyle{ V = \frac{2}{3} \pi a r^2, }[/math]
where a is the arc length of the generatrix).
or alternatively:
- [math]\displaystyle{ V = \frac{4}{3} \tau a^2, }[/math]
where τ is the thickness at the axis of rotation.
Surface area
The surface area S of the balloon is given by
- [math]\displaystyle{ S = \pi^2r^2 }[/math]
where r is the radius of the balloon.
Derivation
Substituting [math]\displaystyle{ u = \arccos(x/r) }[/math] into the parametric equation for z(u) given in § Parametric characterization yields the following equation for z in terms of x:
[math]\displaystyle{ z(x) = r \sqrt{2} \left[ E(\arccos(x/r),\frac{1}{\sqrt{2}})-\frac{1}{2}F(\arccos(x/r), \frac{1}{\sqrt{2}}) \right] }[/math]
The above equation has the following derivative:
[math]\displaystyle{ \frac{dz}{dx} = -\frac{x^2}{\sqrt{r^4 - x^4}} }[/math]
Thus, the surface area is given by the following:
[math]\displaystyle{ S = \int_0^r \! 4\pi x \sqrt{1 + \left(\frac{dz}{dx}\right)^2}\, dx }[/math]
Solving the above integral yields [math]\displaystyle{ S = \pi^2r^2 }[/math].
Surface geometry
The ratio of the principal curvatures at every point on the mylar balloon is exactly 2, making it an interesting case of a Weingarten surface. Moreover, this single property fully characterizes the balloon. The balloon is evidently flatter at the axis of rotation; this point is actually has zero curvature in any direction.
See also
References
- Mladenov, I. M. (2001). "On the Geometry of the Mylar Balloon". C. R. Acad. Bulg. Sci. 54: 39–44. Bibcode: 2001CRABS..54i..39M.
- Paulsen, W. H. (1994). "What Is the Shape of a Mylar Balloon?". American Mathematical Monthly 101 (10): 953–958. doi:10.2307/2975161.
- Finch, Steven (13 August 2013). "Inflating an Inelastic Membrane". http://www.people.fas.harvard.edu/~sfinch/csolve/mylr.pdf.
 |  |
