NM-method

Short description: Statistical NM-method

NM-method

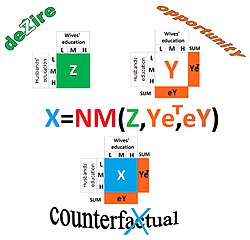
The NM-method or Naszodi–Mendonca method is the operation that can be applied in statistics, econometrics, economics, sociology, and demography to construct counterfactual contingency tables. The method finds the matrix [math]\displaystyle{ X }[/math] ([math]\displaystyle{ X \in \mathbb{R}^{n \times m } }[/math]) which is "closest" to matrix [math]\displaystyle{ Z }[/math] ([math]\displaystyle{ Z \in \mathbb{N}^{n \times m } }[/math] called the seed table) in the sense of being ranked the same but with the row and column totals of a target matrix [math]\displaystyle{ Y }[/math] [math]\displaystyle{ ( Y \in \mathbb{N}^{n \times m }) }[/math]. While the row totals and column totals of [math]\displaystyle{ Y }[/math] are known, matrix [math]\displaystyle{ Y }[/math] itself may not be known.

Since the solution for matrix [math]\displaystyle{ X }[/math] is unique, the NM-method is a function: [math]\displaystyle{ X=\text{NM}(Z, Y e^T_m, e_nY): \mathbb{N}^{n \times m} \times \mathbb{N}^{n} \times \mathbb{N}^{m} \mapsto \mathbb{R}^{n \times m} }[/math], where [math]\displaystyle{ e_n }[/math] is a row vector of size [math]\displaystyle{ 1\times n }[/math], while [math]\displaystyle{ e^T_m }[/math] is a column vector of size [math]\displaystyle{ m\times 1 }[/math].

The NM-method was developed by Naszodi and Mendonca (2021) (and first applied by Naszodi and Mendonca (2019)) to solve for matrix [math]\displaystyle{ X }[/math] in problems, where matrix [math]\displaystyle{ \boldsymbol{Z} }[/math] is not a sample from the population characterized by the row totals and column totals of matrix [math]\displaystyle{ Y }[/math], but represents another population.

Their application aimed at quantifying intergenerational changes in the strength of educational homophily and thus measuring the historical change in social inequality between different educational groups in the US between 1980 and 2010. The trend in inequality was found to be U-shaped, supporting the view that with appropriate social and economic policies inequality can be reduced.

Definition of matrix ranking

The closeness between two matrices of the same size can be defined in several ways. The Euclidean distance, and the Kullback-Leibler divergence are two well-known examples.

The NM-method is consistent with a definition relying on the ordinal Liu-Lu index which is the slightly modified version of the Coleman-index defined by Eq. (15) in Coleman (1958). According to this definition, matrix [math]\displaystyle{ X }[/math] is "closest" to matrix [math]\displaystyle{ Z }[/math], if their Liu-Lu values are the same. In other words, if they are ranked the same by the ordinal Liu-Lu index.

If [math]\displaystyle{ Z }[/math] is a 2×2 matrix, its scalar-valued Liu-Lu index is defined as

[math]\displaystyle{ \text{LL}(Z)=\frac{Z_{1,1}-Q^-(Z_{1,1})}{ \text{min}(Z_{1,.} , Z_{.,1}) -Q^-(Z_{1,1})} }[/math] , where [math]\displaystyle{ Z_{1,.}= Z_{1,1}+ Z_{1,2} }[/math]; [math]\displaystyle{ Z_{.,1}= Z_{1,1}+ Z_{2,1} }[/math]; [math]\displaystyle{ Z_{.,.}=Z_{.,1}+Z_{1,.} }[/math]; [math]\displaystyle{ Q(Z_{1,1})={Z_{1,.} Z_{.,1}}/{Z_{.,.}} }[/math]; [math]\displaystyle{ Q^-(Z_{1,1})=int[Q(Z_{1,1})] }[/math].

Following Coleman (1958), this index is interpreted as the “actual minus expected over maximum minus minimum”, where [math]\displaystyle{ Z_{1,1} }[/math] is the actual value of the [math]\displaystyle{ 1,1 }[/math] entry of the seed matrix [math]\displaystyle{ Z }[/math]; [math]\displaystyle{ Q^- }[/math] is its expected (integer) value under the counterfactual assumptions that the corresponding row total and column total of [math]\displaystyle{ Z }[/math] are predetermined, while its interior is random. Also, [math]\displaystyle{ Q^- }[/math] is its minimum value if the association between the row variable and the column variable of [math]\displaystyle{ Z }[/math] is non-negative. Finally, [math]\displaystyle{ \text{min}(Z_{1,.} , Z_{.,1}) }[/math] is the maximum value of [math]\displaystyle{ Z_{1,1} }[/math] ([math]\displaystyle{ Z \in \mathbb{N}^{n \times m } }[/math]) for given row total [math]\displaystyle{ Z_{1,.} }[/math] and column total [math]\displaystyle{ Z_{.,1} }[/math].

For matrix [math]\displaystyle{ Z }[/math] of size n×m ([math]\displaystyle{ n \geq 2 }[/math], [math]\displaystyle{ m \geq 2 }[/math]), the Liu-Lu index was generalized by Naszodi and Mendonca (2021) to a matrix-valued index. One of the preconditions for the generalization is that the row variable and the column variable of matrix [math]\displaystyle{ Z }[/math] have to be ordered. Equating the generalized, matrix-valued Liu-Lu index of [math]\displaystyle{ Z }[/math] with that of matrix [math]\displaystyle{ X }[/math] is equivalent to dichotomizing their ordered row variable and ordered column variable in [math]\displaystyle{ (n-1) \times (m-1) }[/math] ways by explointing the ordered nature of the row and column variables. Than, equating the original, scalar-valued Liu-Lu indices of the 2×2 matrices obtained with the dichotomizations. I.e., for any pair of [math]\displaystyle{ i,j }[/math] ([math]\displaystyle{ i \in \{1, \ldots, n-1 \} }[/math], and [math]\displaystyle{ j \in \{1, \ldots, m-1 \} }[/math]) the restriction [math]\displaystyle{ \text{LL}(V_i X W^T_j) = \text{LL}(V_i Z W^T_j) }[/math] is imposed, where [math]\displaystyle{ V_i }[/math] is the [math]\displaystyle{ 2 \times n }[/math] matrix [math]\displaystyle{ V_i=\begin{bmatrix} \color{red}1 & \color{red}\cdots & \color{red}1 & \color{blue}0 & \color{blue}\cdots & \color{blue}0 \\ \color{red}0 & \color{red}\cdots & \color{red}0 & \color{blue}1 & \color{blue}\cdots & \color{blue}1 \end{bmatrix} }[/math] with its first block being of size [math]\displaystyle{ 2 \times i }[/math], and its second block being of size [math]\displaystyle{ 2 \times (n-i) }[/math]. Similarly, [math]\displaystyle{ W^T_j }[/math] is the [math]\displaystyle{ m \times 2 }[/math] matrix given by the transpose of [math]\displaystyle{ W_j=\begin{bmatrix} \color{red}1 & \color{red}\cdots & \color{red}1 & \color{blue}0 & \color{blue}\cdots & \color{blue}0 \\ \color{red}0 & \color{red}\cdots & \color{red}0 & \color{blue}1 & \color{blue}\cdots & \color{blue}1 \end{bmatrix} }[/math] with its first block being of size [math]\displaystyle{ 2 \times j }[/math], and its second block being of size [math]\displaystyle{ 2 \times (m-j) }[/math].

Constraints on the row totals and column totals

Matrix [math]\displaystyle{ X }[/math] should satisfy not only [math]\displaystyle{ \text{LL}(V_i X W^T_j)= \text{LL}(V_i Z W^T_j) }[/math] but also the pair of constraints on its row totals and column totals: [math]\displaystyle{ Xe^T_m=Ye^T_m }[/math] and [math]\displaystyle{ e_n X=e_n Y }[/math].

Solution

Assuming that [math]\displaystyle{ \text{LL}(V_i Z W^T_j) \geq 0 }[/math] for all pairs of [math]\displaystyle{ i,j }[/math] (where [math]\displaystyle{ i \in \{1, \ldots, n-1 \} }[/math], and [math]\displaystyle{ j \in \{1, \ldots, m-1 \} }[/math]), the solution for [math]\displaystyle{ X }[/math] is unique, deterministic, and given by a closed-form formula.

For matrices [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Z }[/math] of size [math]\displaystyle{ \boldsymbol{2\times 2} }[/math], the solution is

[math]\displaystyle{ X_{1,1} = \frac{\left[ Z_{1,1} - \text{int}\left({Z_{1,\cdot} Z_{\cdot,1}}/{Z_{\cdot,\cdot}}\right)\right] \left[{\text{min}\left(Y_{1,\cdot} , Y_{\cdot,1} \right)- \text{int}\left({Y_{1,\cdot}Y_{\cdot,1}}/ {Y_{\cdot,\cdot}} \right) }\right] }{\text{min}\left(Z_{1,\cdot}, Z_{\cdot,1} \right)- \text{int}\left({Z_{1,\cdot}Z_{\cdot,1}}/{Z_{\cdot,\cdot}} \right) } +\text{int}\left({Y_{1,\cdot} Y_{\cdot,1}}/{Y_{\cdot,\cdot}}\right) }[/math].

The other 3 cells of [math]\displaystyle{ X }[/math] are uniquely determined by the row totals and column totals. So, this is how the NM-method works for 2×2 seed tables.

For [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] matrices of size [math]\displaystyle{ \boldsymbol{n\times m} }[/math] ([math]\displaystyle{ n \geq 2 }[/math], [math]\displaystyle{ m \geq 2 }[/math]), the solution is obtained by dichotomizing their ordered row variable and ordered column variable in all possible meaningful ways before solving [math]\displaystyle{ (n-1)(m-1) }[/math] number of problems of 2×2 form. Each problem is defined for an [math]\displaystyle{ i,j }[/math] pair ([math]\displaystyle{ i \in \{1,..., n-1\} }[/math] and [math]\displaystyle{ j \in \{1,..., m-1\} }[/math]) with [math]\displaystyle{ \text{LL}(V_i X W^T_j)= \text{LL}(V_i Z W^T_j) }[/math], and the target row totals and column totals: [math]\displaystyle{ V_i X e^T_{m}= V_i Y e^T_{m} }[/math], and [math]\displaystyle{ e_{n} X W^T_j = e_{n} Y W^T_j }[/math], respectively. Each problem is to be solved separately by the formula for [math]\displaystyle{ X_{1,1} }[/math]. The set of solutions determine [math]\displaystyle{ (n-1) (m-1) }[/math] number of entries of matrix [math]\displaystyle{ X }[/math]. Its remaining [math]\displaystyle{ m+n-1 }[/math] elements are uniquely determined by the target row totals and column totals.

Next, let us see how the NM-method works if matrix [math]\displaystyle{ Z }[/math] is such that the second precondition of [math]\displaystyle{ \boldsymbol{\text{LL}(V_i Z W^T_j) \geq 0} }[/math] is not met for [math]\displaystyle{ \boldsymbol{\forall i,j} }[/math].

If [math]\displaystyle{ \boldsymbol{\text{LL}(V_i Z W^T_j) \leq 0 } }[/math] for all pairs of [math]\displaystyle{ \boldsymbol{i,j} }[/math], the solution for [math]\displaystyle{ X }[/math] is also unique, deterministic, and given by a closed-form formula. However, the corresponding concept of matrix ranking is slightly different from the one discussed above. Liu and Lu (2006) define it as [math]\displaystyle{ \text{LL}^-(Z)=\frac{Z_{1,1}-Q^+(Z_{1,1})}{ Q^+(Z_{1,1})- max(0; Z_{1,.}-Z_{.,2}) } }[/math] , where [math]\displaystyle{ Z_{.,2}= Z_{1,2}+ Z_{2,2} }[/math]; [math]\displaystyle{ Q^+(Z_{1,1}) }[/math] is the smallest integer being larger than or equal to [math]\displaystyle{ Q }[/math].

Finally, neither the NM-method, nor [math]\displaystyle{ \boldsymbol{\text{LL}(Z)} }[/math] is defined if [math]\displaystyle{ \exist (i,j) }[/math] pair such that [math]\displaystyle{ \boldsymbol{\text{LL}(V_i Z W^T_j) \gt 0 } }[/math], while for another pair of [math]\displaystyle{ k,l (\neq i,j) }[/math] [math]\displaystyle{ \boldsymbol{\text{ LL}(V_k Z W^T_l) \lt 0} }[/math].

A numerical example

Consider the following matrix [math]\displaystyle{ \color{green}Z }[/math] complemented with its row totals and column totals and the targets, i.e., the row totals and column totals of matrix [math]\displaystyle{ \color{orange}Y }[/math]:

Z	1	2	3	4	TOTAL	TARGET
1	120	70	30	20	240	400
2	50	100	50	35	235	300
3	30	40	75	40	185	150
4	10	20	30	80	140	150
TOTAL	210	230	185	175	800
TARGET	400	300	200	100		1,000

As a first step of the NM-method, matrix [math]\displaystyle{ \color{green} Z }[/math] is multiplied by the [math]\displaystyle{ \boldsymbol{V_i} }[/math], and [math]\displaystyle{ \boldsymbol{W^T_j} }[/math] matrices for each pair of [math]\displaystyle{ i,j }[/math] ([math]\displaystyle{ i \in \{1, 2, 3 \} }[/math], and [math]\displaystyle{ j \in \{1, 2, 3 \} }[/math]). It yields the following 9 matrices of size 2×2 with their target row totals and column totals:

[math]\displaystyle{ i=1, j=1 }[/math] 1 2 TOTAL TARGET 1 120 120 240 400 2 90 470 560 600 TOTAL 210 590 800 TARGET 400 600 1,000	[math]\displaystyle{ i=1, j=2 }[/math] 1 2 TOTAL TARGET 1 190 50 240 400 2 250 30 560 600 TOTAL 440 360 800 TARGET 700 300 1,000	[math]\displaystyle{ i=1, j=3 }[/math] 1 2 TOTAL TARGET 1 220 20 240 400 2 405 155 560 600 TOTAL 625 175 800 TARGET 900 100 1,000
[math]\displaystyle{ i=2, j=1 }[/math] 1 2 TOTAL TARGET 1 170 305 475 700 2 40 285 325 300 TOTAL 210 590 800 TARGET 400 600 1,000	[math]\displaystyle{ i=2, j=2 }[/math] 1 2 TOTAL TARGET 1 340 135 475 700 2 100 225 325 300 TOTAL 440 360 800 TARGET 700 300 1,000	[math]\displaystyle{ i=2, j=3 }[/math] 1 2 TOTAL TARGET 1 420 55 475 700 2 205 120 325 300 TOTAL 625 175 800 TARGET 900 100 1,000
[math]\displaystyle{ i=3, j=1 }[/math] 1 2 TOTAL TARGET 1 200 460 660 850 2 10 130 140 150 TOTAL 210 590 800 TARGET 400 600 1,000	[math]\displaystyle{ i=3, j=2 }[/math] 1 2 TOTAL TARGET 1 410 250 660 850 2 30 110 140 150 TOTAL 440 360 800 TARGET 700 300 1,000	[math]\displaystyle{ i=3, j=3 }[/math] 1 2 TOTAL TARGET 1 565 95 660 850 2 60 80 140 150 TOTAL 625 175 800 TARGET 900 100 1,000

The next step is to calculate the generalized matrix-valued Liu-Lu index [math]\displaystyle{ \text{LL}({Z}) }[/math], (where [math]\displaystyle{ \text{LL}({Z})_{i,j}=\text{LL}(V_i Z W^T_j) }[/math]) by applying the formula of the original scalar-valued Liu-Lu index to each of the 9 matrices:

[math]\displaystyle{ \text{LL(Z)} }[/math]	[math]\displaystyle{ j=1 }[/math]	[math]\displaystyle{ j=2 }[/math]	[math]\displaystyle{ j=3 }[/math]
[math]\displaystyle{ i=1 }[/math]	0.39	0.54	0.62
[math]\displaystyle{ i=2 }[/math]	0.53	0.44	0.47
[math]\displaystyle{ i=3 }[/math]	0.73	0.61	0.45

Apparently, matrix [math]\displaystyle{ \text{LL}(Z) }[/math] is positive. Therefore, the NM-method is defined. Solving each of the 9 problems of the 2×2 form yields 9 entries of the [math]\displaystyle{ X }[/math] matrix. Its other 7 entries are uniquely determined by the target row totals and column totals. The solution for [math]\displaystyle{ \boldsymbol{X} }[/math] is:

[math]\displaystyle{ {X} }[/math]	1	2	3	4	TOTAL
1	253.1	91.4	40.5	15.1	400
2	91.1	147.1	39.8	21.9	300
3	39.6	36.8	64.2	9.3	150
4	16.2	24.7	55.5	53.6	150
TOTAL	400	300	200	100	1,000

Another numerical example taken from Abbott et al.(2019)

Consider the following matrix [math]\displaystyle{ \color{green}Z }[/math] complemented with its row totals and column totals and the targets, i.e., the row totals and column totals of matrix [math]\displaystyle{ \color{orange}Y }[/math]:

Z	1	2	3	TOTAL	TARGET
1	1,070	270	20	1,360	1,600
2	300	4,980	560	5,840	5,900
3	20	420	2,360	2,800	2,500
TOTAL	1,390	5,670	2,940	10,000
TARGET	1,390	5,670	2,940		10,000

As a first step of the NM-method, matrix [math]\displaystyle{ \color{green} Z }[/math] is multiplied by the [math]\displaystyle{ \boldsymbol{V_i} }[/math], and [math]\displaystyle{ \boldsymbol{W^T_j} }[/math] matrices for each pair of [math]\displaystyle{ i,j }[/math] ([math]\displaystyle{ i \in \{1, 2 \} }[/math], and [math]\displaystyle{ j \in \{1, 2 \} }[/math]). It yields the following 4 matrices of size 2×2 with their target row totals and column totals:

[math]\displaystyle{ i=1, j=1 }[/math] 1 2 TOTAL TARGET 1 1,070 290 1,360 1,600 2 320 8,320 8,640 8,400 TOTAL 1,390 8,610 10,000 TARGET 1,390 8,610 10,000	[math]\displaystyle{ i=1, j=2 }[/math] 1 2 TOTAL TARGET 1 1,340 20 1,360 1,600 2 5,720 2,920 8,640 8,400 TOTAL 7,060 2,940 10,000 TARGET 7,060 2,940 10,000
[math]\displaystyle{ i=2, j=1 }[/math] 1 2 TOTAL TARGET 1 1,370 5,830 7,200 7,500 2 20 2,780 2,800 2,500 TOTAL 1,390 8,610 10,000 TARGET 1,390 8,610 10,000	[math]\displaystyle{ i=2, j=2 }[/math] 1 2 TOTAL TARGET 1 6,620 580 7,200 7,500 2 440 2,360 2,800 2,500 TOTAL 7,060 2,940 10,000 TARGET 7,060 2,940 10,000

The next step is to calculate the generalized matrix-valued Liu-Lu index [math]\displaystyle{ \text{LL}({Z}) }[/math], (where [math]\displaystyle{ \text{LL}({Z})_{i,j}=\text{LL}(V_i Z W^T_j) }[/math]) by applying the formula of the original scalar-valued Liu-Lu index to each of the 4 matrices:

[math]\displaystyle{ \text{LL(Z)} }[/math]	[math]\displaystyle{ j=1 }[/math]	[math]\displaystyle{ j=2 }[/math]
[math]\displaystyle{ i=1 }[/math]	0.75	0.95
[math]\displaystyle{ i=2 }[/math]	0.95	0.78

Apparently, matrix [math]\displaystyle{ \text{LL}(Z) }[/math] is positive. Therefore, the NM-method is defined. Solving each of the 4 problems of the 2×2 form yields 4 entries of the [math]\displaystyle{ X }[/math] matrix. Its other 5 entries are uniquely determined by the target row totals and column totals. The solution for [math]\displaystyle{ \boldsymbol{X} }[/math] is:

[math]\displaystyle{ {X} }[/math]	1	2	3	TOTAL
1	1,101	476	24	1,600
2	271	4,819	809	5,900
3	18	375	2,107	2,500
TOTAL	1,390	5,670	2,940	10,000

Implementation

The NM-method is implemented in Excel, Visual Basic, R, and also in Stata.

Applications

The NM-method can be applied to study various phenomena including assortative mating, intergenerational mobility as a type of social mobility, residential segregation, recruitment and talent management.

In all of these applications, matrices [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] represent joint distributions of one-to-one matched entities (e.g. husbands and wives, or first born children and mothers, or dwellings and main tenants, or CEOs and companies, or chess instructors and their most talended students) characterized either by a dichotomous categorical variable (e.g. taking values vegetarian/non-vegetarian, Grandmaster/or not), or an ordered multinomial categorical variable (e.g. level of final educational attainment, skiers' ability level, income bracket, category of rental fee, credit rating, FIDE titles). Although the NM-method has a wide range of applicability, all the examples to be presented next are about assortative mating along the education level. In these applications, the two preconditions (of ordered trait variable, and positive assortative mating in all educational groups) are not debated to be met.

Assume that matrix [math]\displaystyle{ Z }[/math] characterizes the joint educational distribution of husbands and wives in Zimbabwe, while matrix [math]\displaystyle{ Y }[/math] characterizes the same in Yemen. Matrix [math]\displaystyle{ X }[/math] to be constructed with the NM-method tells us what would be the joint educational distribution of couples in Zimbabwe, if the educational distributions of husbands and wives were the same as in Yemen, while the overall desire for homogamy (also called as aggregate marital preferences in economics, or marital matching social norms/social barriers in sociology) were unchanged.

In a second application, matrices [math]\displaystyle{ Z }[/math] and [math]\displaystyle{ Y }[/math] characterize the same country in two different years. Matrix [math]\displaystyle{ Z }[/math] is the joint educational distribution of American newlyweds in 2040, where the husbands are from Generation Z and being young adults when observed. Matrix [math]\displaystyle{ Y }[/math] is the same but for Generation Y observed in year 2024. By constructing matrix [math]\displaystyle{ X }[/math], one can study in the future what would be the educational distribution among the just married American young couples if they sorted into marriages the same way as the males in Generation Z and their partners do, while the education level were the same as among the males in Generation Y and their partners.

In a third application, matrices [math]\displaystyle{ Z }[/math] and [math]\displaystyle{ Y }[/math] characterize again the same country in two different years. In this application, matrix [math]\displaystyle{ Z }[/math] is the joint educational distribution of Portuguese young couples (where the male partners' age is between 30 and 34 years) in 2011. And [math]\displaystyle{ Y }[/math] is the same but it is observed in year 1981. One may aim to construct matrix [math]\displaystyle{ X }[/math] in order to study what would have been the educational distribution of Portuguese young couples if they had sorted into marriages like their peers did in 2011, while their gender-specific educational distributions were the same as in 1981.

In each of the first two applications, matrix [math]\displaystyle{ X }[/math] represents a counterfactual joint distribution. It can be used to quantify certain ceteris paribus effects. More precisely, to quantify on a cardinal scale the difference between the directly unobservable degree of marital sorting in Zimbabwe and Yemen, or in Generation Z and Generation Y with a counterfactual decomposition. For the decomposition, the counterfactual table [math]\displaystyle{ X }[/math] is used to calculate the contribution of each of the driving forces (i.e., the observed structural availability of potential partners with various education levels determining the opportunities at the population level; and the unobservable non-structural drivers, e.g., aggregate matching preferences, desires, norms, barriers) and that of their interaction (i.e., the effect of changes in aggregate preferences/desires/norms/barriers due to changes in structural availability) to an observable cardinal scaled statistics (e.g. the share of educationally homogamous couples).

The third application was used by Naszodi and Mendonca (2021) as an example for a non-sense counterfactual: the education level has changed so drastically in Portugal over the three decades studied that this counterfactual is impossible to be obtained.

Some features of the NM-method

First, the NM-method does not yield a meaningful solution if it reaches the limit of its applicability. For instance, in the third application, the NM-method signals with a negative entry in matrix [math]\displaystyle{ X }[/math] that the counterfactual is impossible (see: AlternativeMethod_US_1980s_2010s_age3035_main.xls Sheet PT_A1981_P2011_Not_meaningful). In this respect, the NM-method is similar to the linear probability model that signals the same with a predicted probabiity outside the unit interval [math]\displaystyle{ [0,1] }[/math].

Second, the NM-method commutes with merging neighboring categories of the row variable and that of the column variable: [math]\displaystyle{ \text{NM}(M_r Z, M_r Y e^T_m, M_r e_nY)=M_r \text{NM}(Z, Y e^T_m, e_nY) }[/math], where [math]\displaystyle{ M_r }[/math] is the row merging matrix of size [math]\displaystyle{ (n-1) \times n }[/math]; and [math]\displaystyle{ \text{NM}(Z M_c, Y e^T_m M_c, e_n Y M_c)=\text{NM}(Z, Y e^T_m, e_nY) M_c }[/math], where [math]\displaystyle{ M_c }[/math] is the column merging matrix of size [math]\displaystyle{ m \times (m-1) }[/math].

Third, the NM-method works even if there are zero entries in matrix [math]\displaystyle{ Z }[/math].

Comparison with the IPF

The iterative proportional fitting procedure (IPF) is also a function:[math]\displaystyle{ \text{IPF}(Z, Y e^T_m, e_nY): \mathbb{R}^{n \times m} \times \mathbb{R}^{n} \times \mathbb{R}^{m} \mapsto \mathbb{R}^{n \times m} }[/math]. It is the operation of finding the fitted matrix [math]\displaystyle{ \boldsymbol{F} }[/math] ([math]\displaystyle{ F \in \mathbb{R}^{n \times m} }[/math]) which fulfills a set of conditions similar to those met by matrix [math]\displaystyle{ X }[/math] constructed with the NM-method. E.g., matrix [math]\displaystyle{ F }[/math] is the closest to matrix [math]\displaystyle{ \boldsymbol{Z} }[/math] but with the row and column totals of the target matrix [math]\displaystyle{ \boldsymbol{Y} }[/math].

However, there are differences between the IPF and the NM-method. The IPF defines closeness of matrices of the same size by the cross-entropy, or the Kullback-Leibler divergence. Accordingly, the IPF compatible concept of distance between the 2×2 matrices [math]\displaystyle{ F }[/math] and [math]\displaystyle{ Z }[/math] is zero, if their crossproduct ratios (also known as the odds ratio) are the same: [math]\displaystyle{ { F_{1,1} F_{2,2} }/ { F_{1,2} F_{2,1} } ={ Z_{1,1} Z_{2,2} }/ { Z_{1,2} Z_{2,1} } }[/math]. To recall, the NM-method's condition for equal ranking of matrices [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] is [math]\displaystyle{ \text{LL}(X)=\frac{X_{1,1}-int[{X_{1,.} X_{.,1}}/{X_{.,.}}]}{ \text{min}(X_{1,.} , X_{.,1}) -int[{X_{1,.} X_{.,1}}/{X_{.,.}}]} =\frac{Z_{1,1}-int[{Z_{1,.} Z_{.,1}}/{Z_{.,.}}]}{ \text{min}(Z_{1,.} , Z_{.,1}) -int[{Z_{1,.} Z_{.,1}}/{Z_{.,.}}]} =\text{LL}(Z) }[/math].

The following numerical example highlights that the IPF and the NM-method are not identical: [math]\displaystyle{ \text{IPF}(Z, Y e^T_m, e_nY) \neq \text{NM}(Z, Y e^T_m, e_nY) }[/math]. Consider the matrix [math]\displaystyle{ \color{Green}Z }[/math] with its targets:

	1	2	TOTAL	TARGET
1	450	150	600	1,050
2	50	350	400	450
TOTAL	500	500
TARGET	1,000	500		1,500

The NM-method yields the following matrix [math]\displaystyle{ X }[/math]:

[math]\displaystyle{ X }[/math]	1	2	TOTAL
1	925	125	1,050
2	75	375	450
TOTAL	1,000	500	1,500

Whereas the solution for matrix [math]\displaystyle{ F }[/math] obtained with the IPF is:

[math]\displaystyle{ F }[/math]	1	2	TOTAL
1	900	150	1,050
2	100	350	450
TOTAL	1,000	500	1,500

The IPF is equivalent to the maximum likelihood estimator of a joint population distribution, where matrix [math]\displaystyle{ F }[/math] (the estimate for the joint population distribution) is calculated from matrix [math]\displaystyle{ Z }[/math], the observed joint distribution in a random sample taken from the population characterized by the row totals and column totals of matrix [math]\displaystyle{ Y }[/math]. In contrast to the problem solved by the IPF, matrix [math]\displaystyle{ Z }[/math] is not sampled from this population in the problem that the NM-method was developed to solve. In fact, in the NM-problem, matrices [math]\displaystyle{ Z }[/math] and [math]\displaystyle{ Y }[/math] characterize two different populations (either observed simultaneously like in the application for Zimbabwe and Yemen, or observed in two different points in time like in its application for the populations of Generation Z and Generation Y). This difference facilitates the choice between the NM-method and the IPF in empirical applications.

Deming and Stephan(1940), the inventors of the IPF, illustrated the application of their method on a classic maximum likelihood estimation problem, where matrix [math]\displaystyle{ Z }[/math] was sampled from the population characterized by the row totals and column totals of matrix [math]\displaystyle{ Y }[/math]. They were aware of the fact that in general, the IPF is not suitable for counterfactual predictions: they explicitly warned that their algorithm is “not by itself useful for prediction” (see Stephan and Deming 1940 p. 444).

In addition, the domains are different for which the IPF and the NM-method yield solutions. First, unlike the NM-method, the IPF does not provide a solution for all seed tables [math]\displaystyle{ {Z} }[/math] with zero entries (Csiszár (1975) found necessary and sufficient conditions for applying the IPF with general tables having zero entries). Second, unlike the IPF, the NM-method does not provide a meaningful solution for pairs of matrices [math]\displaystyle{ {Z} }[/math] and [math]\displaystyle{ {Y} }[/math] defining impossible counterfactuals. Third, the precondition of the NM-method (of either [math]\displaystyle{ \boldsymbol{\text{LL}(Z)\geq 0} }[/math] or [math]\displaystyle{ \boldsymbol{\text{LL}(Z)\leq 0} }[/math]) is not a precondition for the applicability of the IPF.

Finally, unlike the NM, the IPF does not commute with the operation of merging neighboring categories of the row variable and that of the column variable as it is illustrated with a numerical example in Naszodi(2023) (see page 10). For this reason, the transformed table obtained with the IPF can be sensitive to the choice of the number of trait categories.

Comparison with the Minimum Euclidean Distance Approach

The Minimum Euclidean Distance Approach (MEDA) (defined by Abbott et al., 2019 following Fernández and Rogerson, 2001) is also a function: [math]\displaystyle{ \text{MEDA}(Z, Y e^T_m, e_nY): \mathbb{R}^{n \times m} \times \mathbb{R}^{n} \times \mathbb{R}^{m} \mapsto \mathbb{R}^{n \times m} }[/math].

First, MEDA assigns a scalar to matrix [math]\displaystyle{ Z }[/math]: it is the weight used for constructing the convex combination of two extreme cases (random and perfectly assortative matching with the pair of marginals [math]\displaystyle{ (Z e^T_m, e_nZ) }[/math]) by minimizing the Eucledean distance with [math]\displaystyle{ Z }[/math]. E.g. this scalar is [math]\displaystyle{ v=0.265 }[/math] in the numerical example taken from Abbott et al.(2019). Second, for any pair of counterfactual marginal distributions ([math]\displaystyle{ Y e^T_m, e_nY }[/math]) the MEDA constructs the convex combination of the two extreme cases (random and perfectly assortative matches with the pair of marginals ([math]\displaystyle{ Y e^T_m, e_nY }[/math])).

Differences between the NM and the MEDA: while the NM holds the assortativeness unchanged by keeping the generalized matrix-valued Liu-Lu index [math]\displaystyle{ \text{LL}({Z}) }[/math] fixed, the MEDA does the same by keeping the scalar [math]\displaystyle{ v }[/math] fixed. For [math]\displaystyle{ Y }[/math], and [math]\displaystyle{ Z }[/math] matrices of size [math]\displaystyle{ 2\times 2 }[/math] the two methods produces the same transformed table provided [math]\displaystyle{ v }[/math] ranks the contingency tables the same as the scalar-valued Liu-Lu index does. However, for [math]\displaystyle{ {Z} }[/math] matrices larger that 2×2, the generalized Liu-Lu index is matrix-valued, so it is different from the scalar-valued [math]\displaystyle{ v({Z}) }[/math]. Therefore, the NM-transformed table is also different from the MEDA-transformed table.

For instance, in the numerical example taken from Abbott et al.(2019), the counterfactual table constructed by MEDA is the matrix [math]\displaystyle{ F }[/math]:

[math]\displaystyle{ F }[/math]	1	2	3	TOTAL
1	1,081	240	279	1,600
2	217	5,054	629	5,900
3	92	376	2,032	2,500
TOTAL	1,390	5,670	2,940	10,000

The difference between matrix [math]\displaystyle{ F }[/math] and matrix [math]\displaystyle{ X }[/math] is not negligible. E.g. the share of homogamous couples is 2 percentage points smaller in the MEDA-constructed counterfactual matrix [math]\displaystyle{ F }[/math] than in the observed matrix [math]\displaystyle{ Z }[/math], whereas it is 3.4 percentage points smaller in the NM-constructed counterfactual matrix [math]\displaystyle{ X }[/math] relative to [math]\displaystyle{ Z }[/math].

Because Abbott's example is not a fictional one, but is based on the empirical educational distribution of American couples, therefore the difference between 2 percentage points and 3.4 percentage points can be interpreted as the MEDA quantifies changes in inequality from one generation to another generation to be significantly smaller compared to the NM.

See also

• Iterative proportional fitting procedure
• Generalized Naszodi-Mendonca method (GNM-method)