Oscillation (mathematics)
In mathematics, the oscillation of a function or a sequence is a number that quantifies how much that sequence or function varies between its extreme values as it approaches infinity or a point. As is the case with limits, there are several definitions that put the intuitive concept into a form suitable for a mathematical treatment: oscillation of a sequence of real numbers, oscillation of a real-valued function at a point, and oscillation of a function on an interval (or open set).
Definitions
Oscillation of a sequence
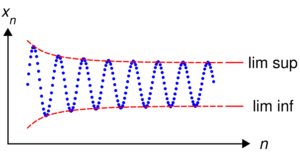
Let [math]\displaystyle{ (a_n) }[/math] be a sequence of real numbers. The oscillation [math]\displaystyle{ \omega(a_n) }[/math] of that sequence is defined as the difference (possibly infinite) between the limit superior and limit inferior of [math]\displaystyle{ (a_n) }[/math]:
- [math]\displaystyle{ \omega(a_n) = \limsup_{n\to\infty} a_n - \liminf_{n\to\infty} a_n }[/math].
The oscillation is zero if and only if the sequence converges. It is undefined if [math]\displaystyle{ \limsup_{n\to\infty} }[/math] and [math]\displaystyle{ \liminf_{n\to\infty} }[/math] are both equal to +∞ or both equal to −∞, that is, if the sequence tends to +∞ or −∞.
Oscillation of a function on an open set
Let [math]\displaystyle{ f }[/math] be a real-valued function of a real variable. The oscillation of [math]\displaystyle{ f }[/math] on an interval [math]\displaystyle{ I }[/math] in its domain is the difference between the supremum and infimum of [math]\displaystyle{ f }[/math]:
- [math]\displaystyle{ \omega_f(I) = \sup_{x\in I} f(x) - \inf_{x\in I} f(x). }[/math]
More generally, if [math]\displaystyle{ f:X\to\mathbb{R} }[/math] is a function on a topological space [math]\displaystyle{ X }[/math] (such as a metric space), then the oscillation of [math]\displaystyle{ f }[/math] on an open set [math]\displaystyle{ U }[/math] is
- [math]\displaystyle{ \omega_f(U) = \sup_{x\in U} f(x) - \inf_{x\in U}f(x). }[/math]
Oscillation of a function at a point
The oscillation of a function [math]\displaystyle{ f }[/math] of a real variable at a point [math]\displaystyle{ x_0 }[/math] is defined as the limit as [math]\displaystyle{ \epsilon\to 0 }[/math] of the oscillation of [math]\displaystyle{ f }[/math] on an [math]\displaystyle{ \epsilon }[/math]-neighborhood of [math]\displaystyle{ x_0 }[/math]:
- [math]\displaystyle{ \omega_f(x_0) = \lim_{\epsilon\to 0} \omega_f(x_0-\epsilon,x_0+\epsilon). }[/math]
This is the same as the difference between the limit superior and limit inferior of the function at [math]\displaystyle{ x_0 }[/math], provided the point [math]\displaystyle{ x_0 }[/math] is not excluded from the limits.
More generally, if [math]\displaystyle{ f:X\to\mathbb{R} }[/math] is a real-valued function on a metric space, then the oscillation is
- [math]\displaystyle{ \omega_f(x_0) = \lim_{\epsilon\to 0} \omega_f(B_\epsilon(x_0)). }[/math]
Examples
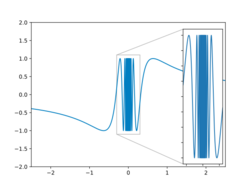
- [math]\displaystyle{ \frac {1}{x} }[/math] has oscillation ∞ at [math]\displaystyle{ x }[/math] = 0, and oscillation 0 at other finite [math]\displaystyle{ x }[/math] and at −∞ and +∞.
- [math]\displaystyle{ \sin \frac {1}{x} }[/math] (the topologist's sine curve) has oscillation 2 at [math]\displaystyle{ x }[/math] = 0, and 0 elsewhere.
- [math]\displaystyle{ \sin x }[/math] has oscillation 0 at every finite [math]\displaystyle{ x }[/math], and 2 at −∞ and +∞.
- [math]\displaystyle{ (-1)^x }[/math]or 1, -1, 1, -1, 1, -1... has oscillation 2.
In the last example the sequence is periodic, and any sequence that is periodic without being constant will have non-zero oscillation. However, non-zero oscillation does not usually indicate periodicity.
Geometrically, the graph of an oscillating function on the real numbers follows some path in the xy-plane, without settling into ever-smaller regions. In well-behaved cases the path might look like a loop coming back on itself, that is, periodic behaviour; in the worst cases quite irregular movement covering a whole region.
Continuity
Oscillation can be used to define continuity of a function, and is easily equivalent to the usual ε-δ definition (in the case of functions defined everywhere on the real line): a function ƒ is continuous at a point x0 if and only if the oscillation is zero;[1] in symbols, [math]\displaystyle{ \omega_f(x_0) = 0. }[/math] A benefit of this definition is that it quantifies discontinuity: the oscillation gives how much the function is discontinuous at a point.
For example, in the classification of discontinuities:
- in a removable discontinuity, the distance that the value of the function is off by is the oscillation;
- in a jump discontinuity, the size of the jump is the oscillation (assuming that the value at the point lies between these limits from the two sides);
- in an essential discontinuity, oscillation measures the failure of a limit to exist.
This definition is useful in descriptive set theory to study the set of discontinuities and continuous points – the continuous points are the intersection of the sets where the oscillation is less than ε (hence a Gδ set) – and gives a very quick proof of one direction of the Lebesgue integrability condition.[2]
The oscillation is equivalent to the ε-δ definition by a simple re-arrangement, and by using a limit (lim sup, lim inf) to define oscillation: if (at a given point) for a given ε0 there is no δ that satisfies the ε-δ definition, then the oscillation is at least ε0, and conversely if for every ε there is a desired δ, the oscillation is 0. The oscillation definition can be naturally generalized to maps from a topological space to a metric space.
Generalizations
More generally, if f : X → Y is a function from a topological space X into a metric space Y, then the oscillation of f is defined at each x ∈ X by
- [math]\displaystyle{ \omega(x) = \inf\left\{\mathrm{diam}(f(U))\mid U\mathrm{\ is\ a\ neighborhood\ of\ }x\right\} }[/math]
See also
- Wave equation
- Wave envelope
- Grandi's series
- Bounded mean oscillation
References
- ↑ Introduction to Real Analysis, updated April 2010, William F. Trench, Theorem 3.5.2, p. 172
- ↑ Introduction to Real Analysis, updated April 2010, William F. Trench, 3.5 "A More Advanced Look at the Existence of the Proper Riemann Integral", pp. 171–177
Further reading
- Hewitt and Stromberg (1965). Real and abstract analysis. Springer-Verlag. p. 78. ISBN 9780387901381. https://archive.org/details/realabstractanal00hewi_0.
- Oxtoby, J (1996). Measure and category (4th ed.). Springer-Verlag. pp. 31–35. ISBN 978-0-387-90508-2.
- Pugh, C. C. (2002). Real mathematical analysis. New York: Springer. pp. 164–165. ISBN 0-387-95297-7. https://archive.org/details/realmathematical00char/page/164.
 |