PH (complexity)
In computational complexity theory, the complexity class PH is the union of all complexity classes in the polynomial hierarchy:
- [math]\displaystyle{ \mathrm{PH} = \bigcup_{k\in\mathbb{N}} \Delta_k^\mathrm{P} }[/math]
PH was first defined by Larry Stockmeyer.[1] It is a special case of hierarchy of bounded alternating Turing machine. It is contained in P#P = PPP and PSPACE.
PH has a simple logical characterization: it is the set of languages expressible by second-order logic.
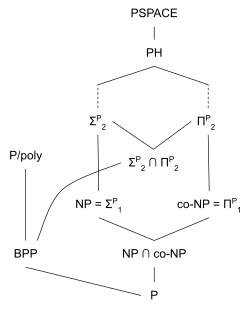
Relationship to other classes
| Unsolved problem in computer science: [math]\displaystyle{ \mathsf{P} \overset{?}{=} \mathsf{NP} }[/math] (more unsolved problems in computer science)
|
| Unsolved problem in computer science: [math]\displaystyle{ \mathsf{PH} \overset{?}{=} \mathsf{PSPACE} }[/math] (more unsolved problems in computer science)
|
PH contains almost all well-known complexity classes inside PSPACE; in particular, it contains P, NP, and co-NP. It even contains probabilistic classes such as BPP[2] (this is the Sipser–Lautemann theorem) and RP. However, there is some evidence that BQP, the class of problems solvable in polynomial time by a quantum computer, is not contained in PH.[3][4]
P = NP if and only if P = PH.[5] This may simplify a potential proof of P ≠ NP, since it is only necessary to separate P from the more general class PH.
PH is a subset of P#P = PPP by Toda's theorem; the class of problems that are decidable by a polynomial time Turing machine with access to a #P or equivalently PP oracle), and also in PSPACE.
Examples
References
- ↑ Stockmeyer, Larry J. (1977). "The polynomial-time hierarchy". Theor. Comput. Sci. 3: 1–22. doi:10.1016/0304-3975(76)90061-X.
- ↑ Lautemann, Clemens (1983-11-08). "BPP and the polynomial hierarchy" (in en). Information Processing Letters 17 (4): 215–217. doi:10.1016/0020-0190(83)90044-3. ISSN 0020-0190. https://dx.doi.org/10.1016/0020-0190%2883%2990044-3.
- ↑ Aaronson, Scott (2009). "Proc. 42nd Symposium on Theory of Computing (STOC 2009)". Association for Computing Machinery. pp. 141–150. doi:10.1145/1806689.1806711. ECCC TR09-104.
- ↑ "Finally, a Problem That Only Quantum Computers Will Ever be Able to Solve". 21 June 2018. https://www.quantamagazine.org/finally-a-problem-that-only-quantum-computers-will-ever-be-able-to-solve-20180621/.
- ↑ Hemaspaandra, Lane (2018). "17.5 Complexity classes". in Rosen, Kenneth H.. Handbook of Discrete and Combinatorial Mathematics. Discrete Mathematics and Its Applications (2nd ed.). CRC Press. pp. 1308–1314. ISBN 9781351644051.
General references
- Bürgisser, Peter (2000). Completeness and reduction in algebraic complexity theory. Algorithms and Computation in Mathematics. 7. Berlin: Springer-Verlag. p. 66. ISBN 3-540-66752-0.
- Complexity Zoo: PH
 |