BQP

In computational complexity theory, bounded-error quantum polynomial time (BQP) is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances. It is the quantum analogue to the complexity class BPP.

A decision problem is a member of BQP if there exists a quantum algorithm (an algorithm that runs on a quantum computer) that solves the decision problem with high probability and is guaranteed to run in polynomial time. A run of the algorithm will correctly solve the decision problem with a probability of at least 2/3.

BQP algorithm (1 run)
Answer produced Correct answer	Yes	No
Yes	≥ 2/3	≤ 1/3
No	≤ 1/3	≥ 2/3
BQP algorithm (k runs)
Answer produced Correct answer	Yes	No
Yes	> 1 − 2−ck	< 2−ck
No	< 2−ck	> 1 − 2−ck
for some constant c > 0

Definition

BQP can be viewed as the languages associated with certain bounded-error uniform families of quantum circuits. A language L is in BQP if and only if there exists a polynomial-time uniform family of quantum circuits $\{Q_n:n\in \mathbb{\mathbb{N}}\}$, such that

• For all $n\in \mathbb{\mathbb{N}}$, Q_n takes n qubits as input and outputs 1 bit
• For all x in L, $\mathrm{P}\mathrm{r}(Q_{|x|}(x)=1)\ge \frac{2}{3}$
• For all x not in L, $\mathrm{P}\mathrm{r}(Q_{|x|}(x)=0)\ge \frac{2}{3}$

Alternatively, one can define BQP in terms of quantum Turing machines. A language L is in BQP if and only if there exists a polynomial quantum Turing machine that accepts L with an error probability of at most 1/3 for all instances.

Similarly to other "bounded error" probabilistic classes, the choice of 1/3 in the definition is arbitrary. We can run the algorithm a constant number of times and take a majority vote to achieve any desired probability of correctness less than 1, using the Chernoff bound. The complexity class is unchanged by allowing error as high as 1/2 − n^−c on the one hand, or requiring error as small as 2^−nc on the other hand, where c is any positive constant, and n is the length of input.

Relationship to other complexity classes

Unsolved problem in computer science: What is the relationship between $\mathsf{B}\mathsf{Q}\mathsf{P}$ and $\mathsf{N}\mathsf{P}$? (more unsolved problems in computer science)

The suspected relationship of BQP to other problem spaces

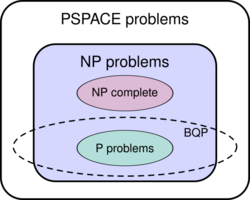
BQP is defined for quantum computers; the corresponding complexity class for classical computers (or more formally for probabilistic Turing machines) is BPP. Just like P and BPP, BQP is low for itself, which means BQP^BQP = BQP. Informally, this is true because polynomial time algorithms are closed under composition. If a polynomial time algorithm calls polynomial time algorithms as subroutines, the resulting algorithm is still polynomial time.

BQP contains P and BPP and is contained in AWPP, PP and PSPACE. In fact, BQP is low for PP, meaning that a PP machine achieves no benefit from being able to solve BQP problems instantly, an indication of the possible difference in power between these similar classes. The known relationships with classic complexity classes are:

$\mathsf{P}\mathsf{\subseteq }\mathsf{B}\mathsf{P}\mathsf{P}\mathsf{\subseteq }\mathsf{B}\mathsf{Q}\mathsf{P}\mathsf{\subseteq }\mathsf{A}\mathsf{W}\mathsf{P}\mathsf{P}\mathsf{\subseteq }\mathsf{P}\mathsf{P}\mathsf{\subseteq }\mathsf{P}\mathsf{S}\mathsf{P}\mathsf{A}\mathsf{C}\mathsf{E}\mathsf{\subseteq }\mathsf{E}\mathsf{X}\mathsf{P}$

As the problem of $\mathsf{P}\stackrel{?}{=}\mathsf{P}\mathsf{S}\mathsf{P}\mathsf{A}\mathsf{C}\mathsf{E}$ has not yet been solved, the proof of inequality between BQP and classes mentioned above is supposed to be difficult. The relation between BQP and NP is not known. In May 2018, computer scientists Ran Raz of Princeton University and Avishay Tal of Stanford University published a paper which showed that, relative to an oracle, BQP was not contained in PH. It can be proven that there exists an oracle A such that ${\mathsf{B}\mathsf{Q}\mathsf{P}}^{\mathrm{A}}⊈{\mathsf{P}\mathsf{H}}^{\mathrm{A}}$. In an extremely informal sense, this can be thought of as giving PH and BQP an identical, but additional, capability and verifying that BQP with the oracle (BQP^A) can do things PH^A cannot. While an oracle separation has been proven, the fact that BQP is not contained in PH has not been proven. An oracle separation does not prove whether or not complexity classes are the same. The oracle separation gives intuition that BQP may not be contained in PH.

It has been suspected for many years that Fourier Sampling is a problem that exists within BQP, but not within the polynomial hierarchy. Recent conjectures have provided evidence that a similar problem, Fourier Checking, also exists in the class BQP without being contained in the polynomial hierarchy. This conjecture is especially notable because it suggests that problems existing in BQP could be classified as harder than NP-Complete problems. Paired with the fact that many practical BQP problems are suspected to exist outside of P (it is suspected and not verified because there is no proof that P ≠ NP), this illustrates the potential power of quantum computing in relation to classical computing.

Adding postselection to BQP results in the complexity class PostBQP which is equal to PP.

A complete problem for Promise-BQP

Promise-BQP is the class of promise problems that can be solved by a uniform family of quantum circuits (i.e., within BQP). Completeness proofs focus on this version of BQP. Similar to the notion of NP-completeness and other complete problems, we can define a complete problem as a problem that is in Promise-BQP and that every other problem in Promise-BQP reduces to it in polynomial time.

APPROX-QCIRCUIT-PROB

The APPROX-QCIRCUIT-PROB problem is complete for efficient quantum computation, and the version presented below is complete for the Promise-BQP complexity class (and not for the total BQP complexity class, for which no complete problems are known). APPROX-QCIRCUIT-PROB's completeness makes it useful for proofs showing the relationships between other complexity classes and BQP.

Given a description of a quantum circuit C acting on n qubits with m gates, where m is a polynomial in n and each gate acts on one or two qubits, and two numbers $\alpha ,\beta \in [0,1],\alpha >\beta$, distinguish between the following two cases:

• measuring the first qubit of the state $C|0{⟩}^{\otimes n}$ yields $|1⟩$ with probability $\ge \alpha$
• measuring the first qubit of the state $C|0{⟩}^{\otimes n}$ yields $|1⟩$ with probability $\le \beta$

Here, there is a promise on the inputs as the problem does not specify the behavior if an instance is not covered by these two cases.

Claim. Any BQP problem reduces to APPROX-QCIRCUIT-PROB.

Proof. Suppose we have an algorithm A that solves APPROX-QCIRCUIT-PROB, i.e., given a quantum circuit C acting on n qubits, and two numbers $\alpha ,\beta \in [0,1],\alpha >\beta$, A distinguishes between the above two cases. We can solve any problem in BQP with this oracle, by setting $\alpha =2/3,\beta =1/3$.

For any $L\in \mathsf{B}\mathsf{Q}\mathsf{P}$, there exists family of quantum circuits $\{Q_n:n\in \mathbb{\mathbb{N}}\}$ such that for all $n\in \mathbb{\mathbb{N}}$, a state $|x⟩$ of $n$ qubits, if $x\in L,Pr(Q_n(|x⟩)=1)\ge 2/3$; else if $x\notin L,Pr(Q_n(|x⟩)=0)\ge 2/3$. Fix an input $|x⟩$ of n qubits, and the corresponding quantum circuit $Q_n$. We can first construct a circuit $C_x$ such that $C_x|0{⟩}^{\otimes n}=|x⟩$. This can be done easily by hardwiring $|x⟩$ and apply a sequence of CNOT gates to flip the qubits. Then we can combine two circuits to get $C^{\prime }=Q_n{C}_x$, and now $C^{\prime }|0{⟩}^{\otimes n}=Q_n|x⟩$. And finally, necessarily the results of $Q_n$ is obtained by measuring several qubits and apply some (classical) logic gates to them. We can always defer the measurement and reroute the circuits so that by measuring the first qubit of $C^{\prime }|0{⟩}^{\otimes n}=Q_n|x⟩$, we get the output. This will be our circuit C, and we decide the membership of $x\in L$ by running $A(C)$ with $\alpha =2/3,\beta =1/3$. By definition of BQP, we will either fall into the first case (acceptance), or the second case (rejection), so $L\in \mathsf{B}\mathsf{Q}\mathsf{P}$ reduces to APPROX-QCIRCUIT-PROB.

BQP and EXP

We begin with an easier containment. To show that $\mathsf{B}\mathsf{Q}\mathsf{P}\subseteq \mathsf{E}\mathsf{X}\mathsf{P}$, it suffices to show that APPROX-QCIRCUIT-PROB is in EXP since APPROX-QCIRCUIT-PROB is BQP-complete.

Claim — $\text{APPROX-QCIRCUIT-PROB}\in \mathsf{E}\mathsf{X}\mathsf{P}$

Proof

The idea is simple. Since we have exponential power, given a quantum circuit C, we can use classical computer to stimulate each gate in C to get the final state.

More formally, let C be a polynomial sized quantum circuit on n qubits and m gates, where m is polynomial in n. Let $|{\psi }_0⟩=|0{⟩}^{\otimes n}$ and $|{\psi }_i⟩$ be the state after the i-th gate in the circuit is applied to $|{\psi }_{i-1}⟩$. Each state $|{\psi }_i⟩$ can be represented in a classical computer as a unit vector in ${\mathbb{ℂ}}^{2^n}$. Furthermore, each gate can be represented by a matrix in ${\mathbb{ℂ}}^{2^n\times 2^n}$. Hence, the final state $|{\psi }_m⟩$ can be computed in $O(m\cdot 2^{2n})$ time, and therefore all together, we have an $2^{O(n)}$ time algorithm for calculating the final state, and thus the probability that the first qubit is measured to be one. This implies that $\text{APPROX-QCIRCUIT-PROB}\in \mathsf{E}\mathsf{X}\mathsf{P}$.

Note that this algorithm also requires $2^{O(n)}$ space to store the vectors and the matrices. We will show in the following section that we can improve upon the space complexity.

BQP and PSPACE

Sum of histories is a technique introduced by physicist Richard Feynman for path integral formulation. APPROX-QCIRCUIT-PROB can be formulated in the sum of histories technique to show that $\mathsf{B}\mathsf{Q}\mathsf{P}\subseteq \mathsf{P}\mathsf{S}\mathsf{P}\mathsf{A}\mathsf{C}\mathsf{E}$.

Sum of Histories Tree

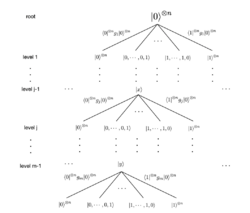
Consider a quantum circuit C, which consists of t gates, $g_1,g_2,\cdots ,g_m$, where each $g_j$ comes from a universal gate set and acts on at most two qubits. To understand what the sum of histories is, we visualize the evolution of a quantum state given a quantum circuit as a tree. The root is the input $|0{⟩}^{\otimes n}$, and each node in the tree has $2^n$ children, each representing a state in ${\mathbb{ℂ}}^n$. The weight on a tree edge from a node in j-th level representing a state $|x⟩$ to a node in $j+1$-th level representing a state $|y⟩$ is $⟨y|g_{j+1}|x⟩$, the amplitude of $|y⟩$ after applying $g_{j+1}$ on $|x⟩$. The transition amplitude of a root-to-leaf path is the product of all the weights on the edges along the path. To get the probability of the final state being $|\psi ⟩$, we sum up the amplitudes of all root-to-leave paths that ends at a node representing $|\psi ⟩$.

More formally, for the quantum circuit C, its sum over histories tree is a tree of depth m, with one level for each gate $g_i$ in addition to the root, and with branching factor $2^n$.

Define — A history is a path in the sum of histories tree. We will denote a history by a sequence $(u_0=|0{⟩}^{\otimes n}\to u_1\to \cdots \to u_{m-1}\to u_m=x)$ for some final state x.

Define — Let $u,v\in \{0,1{\}}^n$. Let amplitude of the edge $(|u⟩,|v⟩)$ in the j-th level of the sum over histories tree be ${\alpha }_j(u\to v)=⟨v|g_j|u⟩$. For any history $h=(u_0\to u_1\to \cdots \to u_{m-1}\to u_m)$, the transition amplitude of the history is the product ${\alpha }_h={\alpha }_1(|0{⟩}^{\otimes n}\to u_1){\alpha }_2(u_1\to u_2)\cdots {\alpha }_m(u_{m-1}\to x)$.

Claim — For a history $(u_0\to \cdots \to u_m)$ . The transition amplitude of the history is computable in polynomial time.

Proof

Each gate $g_j$ can be decomposed into $g_j=I\otimes {\tilde{g}}_j$ for some unitary operator ${\tilde{g}}_j$ acting on two qubits, which without loss of generality can be taken to be the first two. Hence, $⟨v|g_j|u⟩=⟨v_1,v_2|{\tilde{g}}_j|u_1,u_2⟩⟨v_3,\cdots ,v_n|u_3,\cdots ,u_n⟩$ which can be computed in polynomial time in n. Since m is polynomial in n, the transition amplitude of the history can be computed in polynomial time.

Claim — Let $C|0{⟩}^{\otimes n}=\sum _{x\in \{0,1{\}}^n}{\alpha }_x|x⟩$ be the final state of the quantum circuit. For some $x\in \{0,1{\}}^n$, the amplitude ${\alpha }_x$ can be computed by ${\alpha }_x=\sum _{h=(|0{⟩}^{\otimes n}\to u_1\to \cdots \to u_{t-1}\to |x⟩)}{\alpha }_h$.

Proof

We have ${\alpha }_x=⟨x|C|0{⟩}^{\otimes n}=⟨x|g_t{g}_{t-1}\cdots g_1|C|0{⟩}^{\otimes n}$. The result comes directly by inserting $I=\sum _{x\in \{0,1{\}}^n}|x⟩⟨x|$ between $g_1,g_2$, and $g_2,g_3$, and so on, and then expand out the equation. Then each term corresponds to a ${\alpha }_h$, where $h=(|0{⟩}^{\otimes n}\to u_1\to \cdots \to u_{t-1}\to |x⟩)$

Claim — $\text{APPROX-QCIRCUIT-PROB}\in \mathsf{P}\mathsf{S}\mathsf{P}\mathsf{A}\mathsf{C}\mathsf{E}$

Notice in the sum over histories algorithm to compute some amplitude ${\alpha }_x$, only one history is stored at any point in the computation. Hence, the sum over histories algorithm uses $O(nm)$ space to compute ${\alpha }_x$ for any x since $O(nm)$ bits are needed to store the histories in addition to some workspace variables.

Therefore, in polynomial space, we may compute $\sum _x|{\alpha }_x{|}^2$ over all x with the first qubit being 1, which is the probability that the first qubit is measured to be 1 by the end of the circuit.

Notice that compared with the simulation given for the proof that $\mathsf{B}\mathsf{Q}\mathsf{P}\subseteq \mathsf{E}\mathsf{X}\mathsf{P}$, our algorithm here takes far less space but far more time instead. In fact it takes $O(m\cdot 2^{mn})$ time to calculate a single amplitude!

BQP and PP

A similar sum-over-histories argument can be used to show that $\mathsf{B}\mathsf{Q}\mathsf{P}\subseteq \mathsf{P}\mathsf{P}$.

P and BQP

We know $\mathsf{P}\subseteq \mathsf{B}\mathsf{Q}\mathsf{P}$, since every classical circuit can be simulated by a quantum circuit.

It is conjectured that BQP solves hard problems outside of P, specifically, problems in NP. The claim is indefinite because we don't know if P=NP, so we don't know if those problems are actually in P. Below are some evidence of the conjecture:

• Integer factorization (see Shor's algorithm)
• Discrete logarithm
• Simulation of quantum systems (see universal quantum simulator)
• Approximating the Jones polynomial at certain roots of unity
• Harrow-Hassidim-Lloyd (HHL) algorithm

See also

• Hidden subgroup problem
• Polynomial hierarchy (PH)
• Quantum complexity theory
• QMA, the quantum equivalent to NP.
• QIP, the quantum equivalent to IP.

External links

• Complexity Zoo link to BQP