Partition algebra
The partition algebra is an associative algebra with a basis of set-partition diagrams and multiplication given by diagram concatenation.[1] Its subalgebras include diagram algebras such as the Brauer algebra, the Temperley–Lieb algebra, or the group algebra of the symmetric group. Representations of the partition algebra are built from sets of diagrams and from representations of the symmetric group.
Definition
Diagrams
A partition of [math]\displaystyle{ 2k }[/math] elements labelled [math]\displaystyle{ 1,\bar 1, 2,\bar 2,\dots, k,\bar k }[/math] is represented as a diagram, with lines connecting elements in the same subset. In the following example, the subset [math]\displaystyle{ \{\bar 1, \bar 4,\bar 5, 6\} }[/math] gives rise to the lines [math]\displaystyle{ \bar 1 - \bar 4, \bar 4 -\bar 5, \bar 5 - 6 }[/math], and could equivalently be represented by the lines [math]\displaystyle{ \bar 1- 6, \bar 4 - 6, \bar 5 - 6, \bar 1 - \bar 5 }[/math] (for instance).
For [math]\displaystyle{ n\in \mathbb{C} }[/math] and [math]\displaystyle{ k\in \mathbb{N}^* }[/math], the partition algebra [math]\displaystyle{ P_k(n) }[/math] is defined by a [math]\displaystyle{ \mathbb{C} }[/math]-basis made of partitions, and a multiplication given by diagram concatenation. The concatenated diagram comes with a factor [math]\displaystyle{ n^D }[/math], where [math]\displaystyle{ D }[/math] is the number of connected components that are disconnected from the top and bottom elements.
Generators and relations
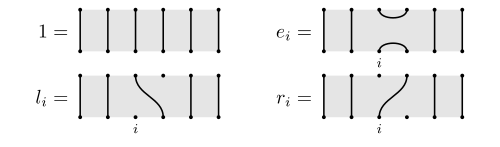
The partition algebra [math]\displaystyle{ P_k(n) }[/math] is generated by [math]\displaystyle{ 3k-2 }[/math] elements of the type
These generators obey relations that include[2]
- [math]\displaystyle{ s_i^2 = 1 \quad , \quad s_is_{i+1}s_i = s_{i+1}s_is_{i+1} \quad, \quad p_i^2 = np_i \quad , \quad b_i^2= b_i \quad , \quad p_i b_i p_i = p_i }[/math]
Other elements that are useful for generating subalgebras include
In terms of the original generators, these elements are
- [math]\displaystyle{ e_i = b_ip_ip_{i+1}b_i \quad , \quad l_i = s_ip_i \quad , \quad r_i=p_is_i }[/math]
Properties
The partition algebra [math]\displaystyle{ P_k(n) }[/math] is an associative algebra. It has a multiplicative identity
The partition algebra [math]\displaystyle{ P_k(n) }[/math] is semisimple for [math]\displaystyle{ n\in\mathbb{C} - \{0,1,\dots, 2k-2\} }[/math]. For any two [math]\displaystyle{ n,n' }[/math] in this set, the algebras [math]\displaystyle{ P_k(n) }[/math] and [math]\displaystyle{ P_k(n') }[/math] are isomorphic.[1]
The partition algebra is finite-dimensional, with [math]\displaystyle{ \dim P_k(n) = B_{2k} }[/math] (a Bell number).
Subalgebras
Eight subalgebras
Subalgebras of the partition algebra can be defined by the following properties:[3]
- Whether they are planar i.e. whether lines may cross in diagrams.
- Whether subsets are allowed to have any size [math]\displaystyle{ 1,2,\dots,2k }[/math], or size [math]\displaystyle{ 1,2 }[/math], or only size [math]\displaystyle{ 2 }[/math].
- Whether we allow top-top and bottom-bottom lines, or only top-bottom lines. In the latter case, the parameter [math]\displaystyle{ n }[/math] is absent, or can be eliminated by [math]\displaystyle{ p_i\to \frac{1}{n}p_i }[/math].
Combining these properties gives rise to 8 nontrivial subalgebras, in addition to the partition algebra itself:[1][3]
| Notation | Name | Generators | Dimension | Example |
|---|---|---|---|---|
| [math]\displaystyle{ P_k(n) }[/math] | Partition | 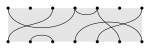[math]\displaystyle{ s_i,p_i,b_i }[/math] | [math]\displaystyle{ B_{2k} }[/math] | 
|
| [math]\displaystyle{ PP_k(n) }[/math] | Planar partition | [math]\displaystyle{ p_i, b_i }[/math] | [math]\displaystyle{ \frac{1}{2k+1}\binom{4k}{2k} }[/math] | 
|
| [math]\displaystyle{ RB_k(n) }[/math] | Rook Brauer | 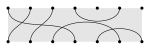[math]\displaystyle{ s_i, e_i, p_i }[/math] | [math]\displaystyle{ \sum_{\ell=0}^k \binom{2k}{2\ell} (2\ell-1)!! }[/math] | 
|
| [math]\displaystyle{ M_k(n) }[/math] | Motzkin | [math]\displaystyle{ e_i, l_i, r_i }[/math] | [math]\displaystyle{ \sum_{\ell=0}^k \frac{1}{\ell+1} \binom{2\ell}{\ell} \binom{2k}{2\ell} }[/math] | 
|
| [math]\displaystyle{ B_k(n) }[/math] | Brauer | [math]\displaystyle{ s_i, e_i }[/math] | [math]\displaystyle{ (2k-1)!! }[/math] | 
|
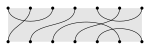
| [math]\displaystyle{ TL_k(n) }[/math] | Temperley–Lieb | 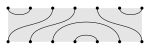[math]\displaystyle{ e_i }[/math] | [math]\displaystyle{ \frac{1}{k+1} \binom{2k}{k} }[/math] | 
|
| [math]\displaystyle{ R_k }[/math] | Rook | [math]\displaystyle{ s_i, p_i }[/math] | [math]\displaystyle{ \sum_{\ell=0}^k \binom{k}{\ell}^2 \ell! }[/math] | 
|
| [math]\displaystyle{ PR_k }[/math] | Planar rook | [math]\displaystyle{ l_i, r_i }[/math] | [math]\displaystyle{ \binom{2k}{k} }[/math] | 
|
| [math]\displaystyle{ \mathbb{C} S_k }[/math] | Symmetric group | 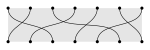[math]\displaystyle{ s_i }[/math] | [math]\displaystyle{ k! }[/math] | 
|
The symmetric group algebra [math]\displaystyle{ \mathbb{C} S_k }[/math] is the group ring of the symmetric group [math]\displaystyle{ S_k }[/math] over [math]\displaystyle{ \mathbb{C} }[/math]. The Motzkin algebra is sometimes called the dilute Temperley–Lieb algebra in the physics literature.[4]
Properties
The listed subalgebras are semisimple for [math]\displaystyle{ n\in\mathbb{C} - \{0,1,\dots, 2k-2\} }[/math].
Inclusions of planar into non-planar algebras:
- [math]\displaystyle{ PP_k(n) \subset P_k(n) \quad , \quad M_k(n) \subset RB_k(n) \quad ,\quad TL_k(n)\subset B_k(n) \quad, \quad PR_k \subset R_k }[/math]
Inclusions from constraints on subset size:
- [math]\displaystyle{ B_k(n) \subset RB_k(n) \subset P_k(n) \quad ,\quad TL_k(n) \subset M_k(n) \subset PP_k(n) \quad , \quad \mathbb{C}S_k \subset R_k }[/math]
Inclusions from allowing top-top and bottom-bottom lines:
- [math]\displaystyle{ R_k \subset RB_k(n) \quad , \quad PR_k\subset M_k(n) \quad ,\quad \mathbb{C}S_k \subset B_k(n) }[/math]
We have the isomorphism:
- [math]\displaystyle{ PP_k(n^2) \cong TL_{2k}(n) \quad , \quad \left\{\begin{array}{l} p_i \mapsto n e_{2i-1} \\ b_i \mapsto \frac{1}{n} e_{2i} \end{array}\right. }[/math]
More subalgebras
In addition to the eight subalgebras described above, other subalgebras have been defined:
- The totally propagating partition subalgebra [math]\displaystyle{ \text{prop}P_k }[/math] is generated by diagrams whose blocks all propagate, i.e. partitions whose subsets all contain top and bottom elements.[5] These diagrams from the dual symmetric inverse monoid, which is generated by [math]\displaystyle{ s_i, b_ip_{i+1}b_{i+1} }[/math].[6]
- The quasi-partition algebra [math]\displaystyle{ QP_k(n) }[/math] is generated by subsets of size at least two. Its generators are [math]\displaystyle{ s_i,b_i,e_i }[/math] and its dimension is [math]\displaystyle{ 1+\sum_{j=1}^{2k} (-1)^{j-1} B_{2k-j} }[/math].[7]
- The uniform block permutation algebra [math]\displaystyle{ U_k }[/math] is generated by subsets with as many top elements as bottom elements. It is generated by [math]\displaystyle{ s_i, b_i }[/math].[8]
An algebra with a half-integer index [math]\displaystyle{ k+\frac12 }[/math] is defined from partitions of [math]\displaystyle{ 2k+2 }[/math] elements by requiring that [math]\displaystyle{ k+1 }[/math] and [math]\displaystyle{ \overline{k+1} }[/math] are in the same subset. For example, [math]\displaystyle{ P_{k+\frac12} }[/math] is generated by [math]\displaystyle{ s_{i\leq k-1},b_{i\leq k},p_{i\leq k} }[/math] so that [math]\displaystyle{ P_k\subset P_{k+\frac12}\subset P_{k+1} }[/math], and [math]\displaystyle{ \dim P_{k+\frac12} =B_{2k+1} }[/math].[2]
Periodic subalgebras are generated by diagrams that can be drawn on an annulus without line crossings. Such subalgebras include a translation element [math]\displaystyle{ u= }[/math]
such that [math]\displaystyle{ u^k=1 }[/math]. The translation element and its powers are the only combinations of [math]\displaystyle{ s_i }[/math] that belong to periodic subalgebras.
Representations
Structure
For an integer [math]\displaystyle{ 0\leq \ell \leq k }[/math], let [math]\displaystyle{ D_\ell }[/math] be the set of partitions of [math]\displaystyle{ k+\ell }[/math] elements [math]\displaystyle{ 1,2,\dots, k }[/math] (bottom) and [math]\displaystyle{ \bar 1,\bar 2,\dots,\bar \ell }[/math] (top), such that no two top elements are in the same subset, and no top element is alone. Such partitions are represented by diagrams with no top-top lines, with at least one line for each top element. For example, in the case [math]\displaystyle{ k=12, \ell = 5 }[/math]:
Partition diagrams act on [math]\displaystyle{ D_\ell }[/math] from the bottom, while the symmetric group [math]\displaystyle{ S_\ell }[/math] acts from the top. For any Specht module [math]\displaystyle{ V_\lambda }[/math] of [math]\displaystyle{ S_\ell }[/math] (with therefore [math]\displaystyle{ |\lambda|=\ell }[/math]), we define the representation of [math]\displaystyle{ P_k(n) }[/math]
- [math]\displaystyle{ \mathcal{P}_\lambda = \mathbb{C} D_{|\lambda|}\otimes_{\mathbb{C} S_{|\lambda|}} V_\lambda\ . }[/math]
The dimension of this representation is[1]
- [math]\displaystyle{ \dim\mathcal{P}_\lambda = f_\lambda \sum_{\ell = |\lambda|}^k \left\{ {k\atop \ell} \right\} \binom{\ell}{|\lambda|} \ , }[/math]
where [math]\displaystyle{ \left\{ {k\atop \ell} \right\} }[/math] is a Stirling number of the second kind, [math]\displaystyle{ \binom{\ell}{|\lambda|} }[/math] is a binomial coefficient, and [math]\displaystyle{ f_\lambda = \dim S_\lambda }[/math] is given by the hook length formula.
A basis of [math]\displaystyle{ \mathcal{P}_\lambda }[/math] can be described combinatorially in terms of set-partition tableaux: Young tableaux whose boxes are filled with the blocks of a set partition.[1]
Assuming that [math]\displaystyle{ P_k(n) }[/math] is semisimple, the representation [math]\displaystyle{ \mathcal{P}_\lambda }[/math] is irreducible, and the set of irreducible finite-dimensional representations of the partition algebra is
- [math]\displaystyle{ \text{Irrep}\left(P_k(n)\right) = \left\{ \mathcal{P}_\lambda \right\}_{0\leq |\lambda|\leq k}\ . }[/math]
Representations of subalgebras
Representations of non-planar subalgebras have similar structures as representations of the partition algebra. For example, the Brauer-Specht modules of the Brauer algebra are built from Specht modules, and certain sets of partitions.
In the case of the planar subalgebras, planarity prevents nontrivial permutations, and Specht modules do not appear. For example, a standard module of the Temperley–Lieb algebra is parametrized by an integer [math]\displaystyle{ 0\leq \ell\leq k }[/math] with [math]\displaystyle{ \ell\equiv k\bmod 2 }[/math], and a basis is simply given by a set of partitions.
The following table lists the irreducible representations of the partition algebra and eight subalgebras.[3]
| Algebra | Parameter | Conditions | Dimension |
|---|---|---|---|
| [math]\displaystyle{ P_k(n) }[/math] | [math]\displaystyle{ \lambda }[/math] | [math]\displaystyle{ 0\leq |\lambda|\leq k }[/math] | [math]\displaystyle{ f_\lambda \sum_{\ell = |\lambda|}^k \left\{ {k\atop \ell} \right\} \binom{\ell}{|\lambda|} }[/math] |
| [math]\displaystyle{ PP_k(n) }[/math] | [math]\displaystyle{ \ell }[/math] | [math]\displaystyle{ 0\leq \ell\leq k }[/math] | [math]\displaystyle{ \binom{2k}{k+\ell}-\binom{2k}{k+\ell+1} }[/math] |
| [math]\displaystyle{ RB_k(n) }[/math] | [math]\displaystyle{ \lambda }[/math] | [math]\displaystyle{ 0\leq |\lambda|\leq k }[/math] | [math]\displaystyle{ f_\lambda \binom{k}{|\lambda|} \sum_{m=0}^{\left\lfloor\frac{k-|\lambda|}{2}\right\rfloor} \binom{k-|\lambda|}{2m} (2m-1)!! }[/math] |
| [math]\displaystyle{ M_k(n) }[/math] | [math]\displaystyle{ \ell }[/math] | [math]\displaystyle{ 0\leq \ell\leq k }[/math] | [math]\displaystyle{ \sum_{m=0}^{\left\lfloor\frac{k-\ell}{2}\right\rfloor} \binom{k}{\ell+2m} \left\{\binom{\ell+2m}{m}-\binom{\ell+2m}{m-1}\right\} }[/math] |
| [math]\displaystyle{ B_k(n) }[/math] | [math]\displaystyle{ \lambda }[/math] | [math]\displaystyle{ \begin{array}{c} 0\leq |\lambda|\leq k \\ |\lambda|\equiv k\bmod 2\end{array} }[/math] | [math]\displaystyle{ f_\lambda \binom{k}{|\lambda|} (k-|\lambda|-1)!! }[/math] |
| [math]\displaystyle{ TL_k(n) }[/math] | [math]\displaystyle{ \ell }[/math] | [math]\displaystyle{ \begin{array}{c} 0\leq \ell\leq k \\ \ell\equiv k\bmod 2\end{array} }[/math] | [math]\displaystyle{ \binom{k}{\frac{k+\ell}{2}} -\binom{k}{\frac{k+\ell+2}{2}} }[/math] |
| [math]\displaystyle{ R_k }[/math] | [math]\displaystyle{ \lambda }[/math] | [math]\displaystyle{ 0\leq |\lambda|\leq k }[/math] | [math]\displaystyle{ f_\lambda \binom{k}{|\lambda|} }[/math] |
| [math]\displaystyle{ PR_k }[/math] | [math]\displaystyle{ \ell }[/math] | [math]\displaystyle{ 0\leq \ell\leq k }[/math] | [math]\displaystyle{ \binom{k}{\ell} }[/math] |
| [math]\displaystyle{ \mathbb{C} S_k }[/math] | [math]\displaystyle{ \lambda }[/math] | [math]\displaystyle{ |\lambda|=k }[/math] | [math]\displaystyle{ f_\lambda }[/math] |
The irreducible representations of [math]\displaystyle{ \text{prop}P_k }[/math] are indexed by partitions such that [math]\displaystyle{ 0\lt |\lambda|\leq k }[/math] and their dimensions are [math]\displaystyle{ f_\lambda \left\{ {k\atop |\lambda|} \right\} }[/math].[5] The irreducible representations of [math]\displaystyle{ QP_k }[/math] are indexed by partitions such that [math]\displaystyle{ 0\leq|\lambda|\leq k }[/math].[7] The irreducible representations of [math]\displaystyle{ U_k }[/math] are indexed by sequences of partitions.[8]
Schur-Weyl duality
Assume [math]\displaystyle{ n\in \mathbb{N}^* }[/math]. For [math]\displaystyle{ V }[/math] a [math]\displaystyle{ n }[/math]-dimensional vector space with basis [math]\displaystyle{ v_1,\dots, v_n }[/math], there is a natural action of the partition algebra [math]\displaystyle{ P_k(n) }[/math] on the vector space [math]\displaystyle{ V^{\otimes k} }[/math]. This action is defined by the matrix elements of a partition [math]\displaystyle{ \{1,\bar 1, 2,\bar 2,\dots, k,\bar k\}=\sqcup_h E_h }[/math] in the basis [math]\displaystyle{ (v_{j_1}\otimes \cdots \otimes v_{j_k}) }[/math]:[2]
- [math]\displaystyle{ \left(\sqcup_h E_h\right)_{j_1,j_2,\dots ,j_k}^{j_{\bar 1}, j_{\bar 2},\dots ,j_{\bar k}} = \mathbf{1}_{r,s\in E_h\implies j_r=j_s} \ . }[/math]
This matrix element is one if all indices corresponding to any given partition subset coincide, and zero otherwise. For example, the action of a Temperley–Lieb generator is
- [math]\displaystyle{ e_i \left(v_{j_1}\otimes \cdots \otimes v_{j_i}\otimes v_{j_{i+1}}\otimes \cdots \otimes v_{j_k}\right) = \delta_{j_i,j_{i+1}}\sum_{j=1}^n v_{j_1}\otimes \cdots \otimes v_{j}\otimes v_{j}\otimes \cdots \otimes v_{j_k}\ . }[/math]
Duality between the partition algebra and the symmetric group
Let [math]\displaystyle{ n\geq 2k }[/math] be integer. Let us take [math]\displaystyle{ V }[/math] to be the natural permutation representation of the symmetric group [math]\displaystyle{ S_n }[/math]. This [math]\displaystyle{ n }[/math]-dimensional representation is a sum of two irreducible representations: the standard and trivial representations, [math]\displaystyle{ V=[n-1,1]\oplus [n] }[/math].
Then the partition algebra [math]\displaystyle{ P_k(n) }[/math] is the centralizer of the action of [math]\displaystyle{ S_n }[/math] on the tensor product space [math]\displaystyle{ V^{\otimes k} }[/math],
- [math]\displaystyle{ P_k(n) \cong \text{End}_{S_n}\left(V^{\otimes k}\right)\ . }[/math]
Moreover, as a bimodule over [math]\displaystyle{ P_k(n)\times S_n }[/math], the tensor product space decomposes into irreducible representations as[1]
- [math]\displaystyle{ V^{\otimes k} = \bigoplus_{0\leq |\lambda|\leq k} \mathcal{P}_\lambda \otimes V_{[n-|\lambda|,\lambda]}\ , }[/math]
where [math]\displaystyle{ [n-|\lambda|,\lambda] }[/math] is a Young diagram of size [math]\displaystyle{ n }[/math] built by adding a first row to [math]\displaystyle{ \lambda }[/math], and [math]\displaystyle{ V_{[n-|\lambda|,\lambda]} }[/math] is the corresponding Specht module of [math]\displaystyle{ S_n }[/math].
Dualities involving subalgebras
The duality between the symmetric group and the partition algebra generalizes the original Schur-Weyl duality between the general linear group and the symmetric group. There are other generalizations. In the relevant tensor product spaces, we write [math]\displaystyle{ V_n }[/math] for an irreducible [math]\displaystyle{ n }[/math]-dimensional representation of the first group or algebra:
| Tensor product space | Group or algebra | Dual algebra or group | Comments |
|---|---|---|---|
| [math]\displaystyle{ \left(V_{n-1}\oplus V_1\right)^{\otimes k} }[/math] | [math]\displaystyle{ S_n }[/math] | [math]\displaystyle{ P_k(n) }[/math] | The duality for the full partition algebra |
| [math]\displaystyle{ \left(V_{n-2}\oplus V_1\oplus V_1\right)^{\otimes k} }[/math] | [math]\displaystyle{ S_{n-1} }[/math] | [math]\displaystyle{ P_{k+\frac12}(n) }[/math] | Case of a partition algebra with a half-integer index[2] |
| [math]\displaystyle{ V_n^{\otimes k} }[/math] | [math]\displaystyle{ GL_n(\mathbb{C}) }[/math] | [math]\displaystyle{ S_k }[/math] | The original Schur-Weyl duality |
| [math]\displaystyle{ V_n^{\otimes k} }[/math] | [math]\displaystyle{ O(n) }[/math] | [math]\displaystyle{ B_k(n) }[/math] | Duality between the orthogonal group and the Brauer algebra |
| [math]\displaystyle{ \left(V_n\oplus V_1\right)^{\otimes k} }[/math] | [math]\displaystyle{ O(n) }[/math] | [math]\displaystyle{ RB_k(n+1) }[/math] | Duality between the orthogonal group and the rook Brauer algebra[9] |
| [math]\displaystyle{ V_n^{\otimes k} }[/math] | [math]\displaystyle{ R_n }[/math] | [math]\displaystyle{ \text{prop}P_k }[/math] | Duality between the rook algebra and the totally propagating partition algebra[10][5] |
| [math]\displaystyle{ V_2^{\otimes k} }[/math] | [math]\displaystyle{ gl(1|1) }[/math] | [math]\displaystyle{ PR_{k-1} }[/math] | Duality between a Lie superalgebra and the planar rook algebra[11] |
| [math]\displaystyle{ V_{n-1}^{\otimes k} }[/math] | [math]\displaystyle{ S_n }[/math] | [math]\displaystyle{ QP_k(n) }[/math] | Duality between the symmetric group and the quasi-partition algebra[7] |
| [math]\displaystyle{ V_n^{\otimes r} \otimes \left(V_n^*\right)^{\otimes s} }[/math] | [math]\displaystyle{ GL_n(\mathbb{C}) }[/math] | [math]\displaystyle{ B_{r,s}(n) }[/math] | Duality involving the walled Brauer algebra.[12] |
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Halverson, Tom; Jacobson, Theodore N. (2020). "Set-partition tableaux and representations of diagram algebras" (in en). Algebraic Combinatorics 3 (2): 509–538. doi:10.5802/alco.102. ISSN 2589-5486. https://alco.centre-mersenne.org/item/ALCO_2020__3_2_509_0.
- ↑ 2.0 2.1 2.2 2.3 Halverson, Tom; Ram, Arun (2005). "Partition algebras" (in en). European Journal of Combinatorics 26 (6): 869–921. doi:10.1016/j.ejc.2004.06.005. https://linkinghub.elsevier.com/retrieve/pii/S0195669804000976.
- ↑ 3.0 3.1 3.2 Colmenarejo, Laura; Orellana, Rosa; Saliola, Franco; Schilling, Anne; Zabrocki, Mike (2020). "An insertion algorithm on multiset partitions with applications to diagram algebras" (in en). Journal of Algebra 557: 97–128. doi:10.1016/j.jalgebra.2020.04.010. https://linkinghub.elsevier.com/retrieve/pii/S0021869320301873.
- ↑ Jacobsen, Jesper Lykke; Ribault, Sylvain; Saleur, Hubert (2022). Spaces of states of the two-dimensional O(n) and Potts models.
- ↑ 5.0 5.1 5.2 Mishra, Ashish; Srivastava, Shraddha (2021). "Jucys–Murphy elements of partition algebras for the rook monoid" (in en). International Journal of Algebra and Computation 31 (5): 831–864. doi:10.1142/S0218196721500399. ISSN 0218-1967. https://www.worldscientific.com/doi/abs/10.1142/S0218196721500399.
- ↑ Maltcev, Victor (2007-03-16). "On a new approach to the dual symmetric inverse monoid I*X". arXiv:math/0703478v1.
- ↑ 7.0 7.1 7.2 Daugherty, Zajj; Orellana, Rosa (2014). "The quasi-partition algebra" (in en). Journal of Algebra 404: 124–151. doi:10.1016/j.jalgebra.2013.11.028. https://linkinghub.elsevier.com/retrieve/pii/S0021869314000477.
- ↑ 8.0 8.1 Orellana, Rosa; Saliola, Franco; Schilling, Anne; Zabrocki, Mike (2021-12-27). "Plethysm and the algebra of uniform block permutations". arXiv:2112.13909v1 [math.CO].
- ↑ Halverson, Tom; delMas, Elise (2014-01-02). "Representations of the Rook-Brauer Algebra" (in en). Communications in Algebra 42 (1): 423–443. doi:10.1080/00927872.2012.716120. ISSN 0092-7872. http://www.tandfonline.com/doi/abs/10.1080/00927872.2012.716120.
- ↑ Kudryavtseva, Ganna; Mazorchuk, Volodymyr (2008). "Schur–Weyl dualities for symmetric inverse semigroups" (in en). Journal of Pure and Applied Algebra 212 (8): 1987–1995. doi:10.1016/j.jpaa.2007.12.004. https://linkinghub.elsevier.com/retrieve/pii/S0022404908000169.
- ↑ Benkart, Georgia; Moon, Dongho (2013-05-28). "Planar Rook Algebras and Tensor Representations of 𝔤𝔩(1 | 1)" (in en). Communications in Algebra 41 (7): 2405–2416. doi:10.1080/00927872.2012.658533. ISSN 0092-7872. http://www.tandfonline.com/doi/abs/10.1080/00927872.2012.658533.
- ↑ Cox, Anton; Visscher, De; Doty, Stephen; Martin, Paul (2007-09-06). "On the blocks of the walled Brauer algebra". arXiv:0709.0851v1 [math.RT].
Further reading
- Kauffman, Louis H. (1991) (in en). Knots and Physics. World Scientific. ISBN 978-981-02-0343-6. https://books.google.com/books?id=av05vRwIKIwC.
- Kauffman, Louis H. (1990). "An invariant of regular isotopy" (in en). Transactions of the American Mathematical Society 318 (2): 417–471. doi:10.1090/S0002-9947-1990-0958895-7. ISSN 0002-9947. https://www.ams.org/tran/1990-318-02/S0002-9947-1990-0958895-7/.
 |  |
