Bell number
In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.
The Bell numbers are denoted , where is an integer greater than or equal to zero. Starting with , the first few Bell numbers are
The Bell number counts the number of different ways to partition a set that has exactly elements, or equivalently, the number of equivalence relations on it. also counts the number of different rhyme schemes for -line poems.[1]
As well as appearing in counting problems, these numbers have a different interpretation, as moments of probability distributions. In particular, is the -th moment of a Poisson distribution with mean 1.
Counting
Set partitions
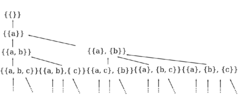

In general, is the number of partitions of a set of size . A partition of a set is defined as a family of nonempty, pairwise disjoint subsets of whose union is . For example, because the 3-element set can be partitioned in 5 distinct ways:
As suggested by the set notation above, the ordering of subsets within the family is not considered; ordered partitions are counted by a different sequence of numbers, the ordered Bell numbers. is 1 because there is exactly one partition of the empty set. This partition is itself the empty set; it can be interpreted as a family of subsets of the empty set, consisting of zero subsets. It is vacuously true that all of the subsets in this family are non-empty subsets of the empty set and that they are pairwise disjoint subsets of the empty set, because there are no subsets to have these unlikely properties.
The partitions of a set correspond one-to-one with its equivalence relations. These are binary relations that are reflexive, symmetric, and transitive. The equivalence relation corresponding to a partition defines two elements as being equivalent when they belong to the same partition subset as each other. Conversely, every equivalence relation corresponds to a partition into equivalence classes.[2] Therefore, the Bell numbers also count the equivalence relations.
Factorizations
If a number is a squarefree positive integer, meaning that it is the product of some number of distinct prime numbers), then gives the number of different multiplicative partitions of . These are factorizations of into numbers greater than one, treating two factorizations as the same if they have the same factors in a different order.[3] For instance, 30 is the product of the three primes 2, 3, and 5, and has = 5 factorizations:
Rhyme schemes
The Bell numbers also count the rhyme schemes of an n-line poem or stanza. A rhyme scheme describes which lines rhyme with each other, and so may be interpreted as a partition of the set of lines into rhyming subsets. Rhyme schemes are usually written as a sequence of Roman letters, one per line, with rhyming lines given the same letter as each other, and with the first lines in each rhyming set labeled in alphabetical order. Thus, the 15 possible four-line rhyme schemes are AAAA, AAAB, AABA, AABB, AABC, ABAA, ABAB, ABAC, ABBA, ABBB, ABBC, ABCA, ABCB, ABCC, and ABCD.[1]
Permutations
The Bell numbers come up in a card shuffling problem mentioned in the addendum to (Gardner 1978). If a deck of n cards is shuffled by repeatedly removing the top card and reinserting it anywhere in the deck (including its original position at the top of the deck), with exactly n repetitions of this operation, then there are nn different shuffles that can be performed. Of these, the number that return the deck to its original sorted order is exactly Bn. Thus, the probability that the deck is in its original order after shuffling it in this way is Bn/nn, which is significantly larger than the 1/n! probability that would describe a uniformly random permutation of the deck.
Related to card shuffling are several other problems of counting special kinds of permutations that are also answered by the Bell numbers. For instance, the nth Bell number equals the number of permutations on n items in which no three values that are in sorted order have the last two of these three consecutive. In a notation for generalized permutation patterns where values that must be consecutive are written adjacent to each other, and values that can appear non-consecutively are separated by a dash, these permutations can be described as the permutations that avoid the pattern 1-23. The permutations that avoid the generalized patterns 12-3, 32-1, 3-21, 1-32, 3-12, 21-3, and 23-1 are also counted by the Bell numbers.[4] The permutations in which every 321 pattern (without restriction on consecutive values) can be extended to a 3241 pattern are also counted by the Bell numbers.[5] However, the Bell numbers grow too quickly to count the permutations that avoid a pattern that has not been generalized in this way: by the (now proven) Stanley–Wilf conjecture, the number of such permutations is singly exponential, and the Bell numbers have a higher asymptotic growth rate than that.
Triangle scheme for calculations

The Bell numbers can easily be calculated by creating the so-called Bell triangle, also called Aitken's array or the Peirce triangle after Alexander Aitken and Charles Sanders Peirce.[6]
- Start with the number one. Put this on a row by itself. ()
- Start a new row with the rightmost element from the previous row as the leftmost number ( where r is the last element of (i-1)-th row)
- Determine the numbers not on the left column by taking the sum of the number to the left and the number above the number to the left, that is, the number diagonally up and left of the number we are calculating
- Repeat step three until there is a new row with one more number than the previous row (do step 3 until )
- The number on the left hand side of a given row is the Bell number for that row. ()
Here are the first five rows of the triangle constructed by these rules:
1 1 2 2 3 5 5 7 10 15 15 20 27 37 52
The Bell numbers appear on both the left and right sides of the triangle.
Properties
Summation formulas
The Bell numbers satisfy a recurrence relation involving binomial coefficients:[7]
It can be explained by observing that, from an arbitrary partition of n + 1 items, removing the set containing the first item leaves a partition of a smaller set of k items for some number k that may range from 0 to n. There are choices for the k items that remain after one set is removed, and Bk choices of how to partition them.
A different summation formula represents each Bell number as a sum of Stirling numbers of the second kind
The Stirling number is the number of ways to partition a set of cardinality n into exactly k nonempty subsets. Thus, in the equation relating the Bell numbers to the Stirling numbers, each partition counted on the left hand side of the equation is counted in exactly one of the terms of the sum on the right hand side, the one for which k is the number of sets in the partition.[8]
(Spivey 2008) has given a formula that combines both of these summations:
Applying Pascal's inversion formula to the recurrence relation, we obtain
Which can be generalized in this manner[9]
Other finite sum formulas using Stirling numbers of the first kind include[9]
Which simplifies down with to
and with to
which can be seen as the inversion formula for Stirling numbers applied to Spivey's formula.
Generating function
The exponential generating function of the Bell numbers is
In this formula, the summation in the middle is the general form used to define the exponential generating function for any sequence of numbers, and the formula on the right is the result of performing the summation in the specific case of the Bell numbers.
One way to derive this result uses analytic combinatorics, a style of mathematical reasoning in which sets of mathematical objects are described by formulas explaining their construction from simpler objects, and then those formulas are manipulated to derive the combinatorial properties of the objects. In the language of analytic combinatorics, a set partition may be described as a set of nonempty urns into which elements labelled from 1 to n have been distributed, and the combinatorial class of all partitions (for all n) may be expressed by the notation
Here, is a combinatorial class with only a single member of size one, an element that can be placed into an urn. The inner operator describes a set or urn that contains one or more labelled elements, and the outer describes the overall partition as a set of these urns. The exponential generating function may then be read off from this notation by translating the operator into the exponential function and the nonemptiness constraint ≥1 into subtraction by one.[10]
An alternative method for deriving the same generating function uses the recurrence relation for the Bell numbers in terms of binomial coefficients to show that the exponential generating function satisfies the differential equation . The function itself can be found by solving this equation.[11][12][13]
Moments of probability distributions
The Bell numbers satisfy Dobinski's formula[14][11][13]
This formula can be derived by expanding the exponential generating function using the Taylor series for the exponential function, and then collecting terms with the same exponent.[10] It allows Bn to be interpreted as the nth moment of a Poisson distribution with expected value 1.
The nth Bell number is also the sum of the coefficients in the nth complete Bell polynomial, which expresses the nth moment of any probability distribution as a function of the first n cumulants.
Modular arithmetic
The Bell numbers obey Touchard's congruence: If p is any prime number then[15]
or, generalizing[16]
Because of Touchard's congruence, the Bell numbers are periodic modulo p, for every prime number p; for instance, for p = 2, the Bell numbers repeat the pattern odd-odd-even with period three. The period of this repetition, for an arbitrary prime number p, must be a divisor of
and for all prime p ≤ 101 and p = 113, 163, 167, or 173 it is exactly this number (sequence A001039 in the OEIS).[17][18]
The period of the Bell numbers to modulo n are
- 1, 3, 13, 12, 781, 39, 137257, 24, 39, 2343, 28531167061, 156, 25239592216021, 411771, 10153, 48, 51702516367896047761, 39, 109912203092239643840221, 9372, 1784341, 85593501183, 949112181811268728834319677753, 312, 3905, 75718776648063, 117, 1647084, 91703076898614683377208150526107718802981, 30459, 568972471024107865287021434301977158534824481, 96, 370905171793, 155107549103688143283, 107197717, 156, ... (sequence A054767 in the OEIS)
Integral representation
An application of Cauchy's integral formula to the exponential generating function yields the complex integral representation
Some asymptotic representations can then be derived by a standard application of the method of steepest descent.[19]
Log-concavity
The Bell numbers form a logarithmically convex sequence. Dividing them by the factorials, Bn/n!, gives a logarithmically concave sequence.[20][21][22]
Growth rate
Several asymptotic formulas for the Bell numbers are known. In (Berend Tassa) the following bounds were established:
- for all positive integers ;
moreover, if then for all ,
where and The Bell numbers can also be approximated using the Lambert W function, a function with the same growth rate as the logarithm, as [23]
(Moser Wyman) established the expansion
uniformly for as , where and each and are known expressions in .[24]
The asymptotic expression
was established by (de Bruijn 1981).
Bell primes
(Gardner 1978) raised the question of whether infinitely many Bell numbers are also prime numbers. The first few Bell numbers that are prime are:
- 2, 5, 877, 27644437, 35742549198872617291353508656626642567, 359334085968622831041960188598043661065388726959079837 (sequence A051131 in the OEIS)
corresponding to the indices 2, 3, 7, 13, 42 and 55 (sequence A051130 in the OEIS).
The next Bell prime is B2841, which is approximately 9.30740105 × 106538.[25] As of 2018[update], it is the largest known prime Bell number. Ignacio Larrosa Cañestro showed it was a probable prime in 2002. After 17 months of computation with Marcel Martin's ECPP program Primo, Ignacio Larrosa Cañestro proved it to be prime in 2004. He ruled out any other possible primes below B6000, later extended to B30447 by Eric Weisstein.[26] The search was extended to B50000 by Václav Kotěšovec (05/18/2021).
History
The Bell numbers are named after Eric Temple Bell, who wrote about them in 1938, following up a 1934 paper in which he studied the Bell polynomials.[27][28] Bell did not claim to have discovered these numbers; in his 1938 paper, he wrote that the Bell numbers "have been frequently investigated" and "have been rediscovered many times". Bell cites several earlier publications on these numbers, beginning with (Dobiński 1877) which gives Dobiński's formula for the Bell numbers. Bell called these numbers "exponential numbers"; the name "Bell numbers" and the notation Bn for these numbers was given to them by (Becker Riordan).[29]
The first exhaustive enumeration of set partitions appears to have occurred in medieval Japan, where (inspired by the popularity of the book The Tale of Genji) a parlor game called genji-ko sprang up, in which guests were given five packets of incense to smell and were asked to guess which ones were the same as each other and which were different. The 52 possible solutions, counted by the Bell number B5, were recorded by 52 different diagrams, which were printed above the chapter headings in some editions of The Tale of Genji.[30][31]
In Srinivasa Ramanujan's second notebook, he investigated both Bell polynomials and Bell numbers.[32] Early references for the Bell triangle, which has the Bell numbers on both of its sides, include (Peirce 1880) and (Aitken 1933).
See also
Notes
- ↑ 1.0 1.1 Gardner 1978.
- ↑ Halmos, Paul R. (1974). Naive set theory. Undergraduate Texts in Mathematics. Springer-Verlag, New York-Heidelberg. pp. 27–28. ISBN 9781475716450. https://books.google.com/books?id=jV_aBwAAQBAJ&pg=PA27.
- ↑ Williams 1945 credits this observation to Silvio Minetola's Principii di Analisi Combinatoria (1909).
- ↑ Claesson (2001).
- ↑ Callan (2006).
- ↑ Sloane, N. J. A., ed. "Sequence A011971 (Aitken's array)". OEIS Foundation. https://oeis.org/A011971.
- ↑ Wilf 1994, p. 23.
- ↑ Conway & Guy (1996).
- ↑ 9.0 9.1 Komatsu, Takao; Pita-Ruiz, Claudio (2018). "Some formulas for Bell numbers" (in en). Filomat 32 (11): 3881–3889. doi:10.2298/FIL1811881K. ISSN 0354-5180. http://www.doiserbia.nb.rs/Article.aspx?ID=0354-51801811881K.
- ↑ 10.0 10.1 Flajolet & Sedgewick 2009.
- ↑ 11.0 11.1 Rota 1964.
- ↑ Wilf 1994, pp. 20-23.
- ↑ 13.0 13.1 Bender & Williamson 2006.
- ↑ Dobiński 1877.
- ↑ Becker & Riordan (1948).
- ↑ Hurst & Schultz (2009).
- ↑ Williams 1945.
- ↑ Wagstaff 1996.
- ↑ Simon, Barry (2010). "Example 15.4.6 (Asymptotics of Bell Numbers)". Complex Analysis. pp. 772–774. http://www.math.caltech.edu/~2010-11/2term/ma111b/CA-Sec15-4_march2.pdf. Retrieved 2012-09-02.
- ↑ Engel 1994.
- ↑ Canfield 1995.
- ↑ Asai, Kubo & Kuo 2000.
- ↑ Lovász (1993).
- ↑ Canfield, Rod (July 1994). "The Moser-Wyman expansion of the Bell numbers". http://www.austinmohr.com/Work_files/bellMoser.pdf.
- ↑ "93074010508593618333...83885253703080601131". 5000 Largest Known Primes, The Prime Database. http://primes.utm.edu/primes/page.php?id=68825.
- ↑ Weisstein, Eric W.. "Integer Sequence Primes". http://mathworld.wolfram.com/IntegerSequencePrimes.html.
- ↑ Bell 1934.
- ↑ Bell 1938.
- ↑ Rota 1964. However, Rota gives an incorrect date, 1934, for Becker & Riordan 1948.
- ↑ Knuth 2013.
- ↑ Gardner 1978 and Berndt 2011 also mention the connection between Bell numbers and The Tale of Genji, in less detail.
- ↑ Berndt 2011.
References
- Asai, Nobuhiro; Kubo, Izumi; Kuo, Hui-Hsiung (2000). "Bell numbers, log-concavity, and log-convexity". Acta Applicandae Mathematicae 63 (1–3): 79–87. doi:10.1023/A:1010738827855.
- "A problem in combinations". Mathematical Notes 28: 18–23. 1933. doi:10.1017/S1757748900002334.
- Becker, H. W.; Riordan, John (1948). "The arithmetic of Bell and Stirling numbers". American Journal of Mathematics 70 (2): 385–394. doi:10.2307/2372336..
- Bell, E. T. (1934). "Exponential polynomials". Annals of Mathematics 35 (2): 258–277. doi:10.2307/1968431..
- Bell, E. T. (1938). "The iterated exponential integers". Annals of Mathematics 39 (3): 539–557. doi:10.2307/1968633..
- Bender, Edward A.; Williamson, S. Gill (2006). "Example 11.7, Set Partitions". Foundations of Combinatorics with Applications. Dover. pp. 319–320. ISBN 0-486-44603-4. http://www.math.ucsd.edu/~ebender/CombText/ch-11.pdf.
- Berend, D.; Tassa, T. (2010). "Improved bounds on Bell numbers and on moments of sums of random variables". Probability and Mathematical Statistics 30 (2): 185–205.
- Berndt, Bruce C. (2011). "Ramanujan Reaches His Hand From His Grave To Snatch Your Theorems From You". Asia Pacific Mathematics Newsletter 1 (2): 8–13. http://www.asiapacific-mathnews.com/01/0102/0008_0013.pdf.
- Asymptotic methods in analysis (3rd ed.). Dover. 1981. p. 108.
- Callan, David (2006). "A combinatorial interpretation of the eigensequence for composition". Journal of Integer Sequences 9 (1): 06.1.4. Bibcode: 2005math......7169C. https://eudml.org/doc/52955.
- Canfield, E. Rodney (1995). "Engel's inequality for Bell numbers". Journal of Combinatorial Theory. Series A 72 (1): 184–187. doi:10.1016/0097-3165(95)90033-0.
- Claesson, Anders (2001). "Generalized pattern avoidance". European Journal of Combinatorics 22 (7): 961–971. doi:10.1006/eujc.2001.0515.
- Conway, John Horton; Guy, Richard K. (1996). "Famous Families of Numbers: Bell Numbers and Stirling Numbers". The Book of Numbers. Copernicus Series. Springer. pp. 91–94. ISBN 9780387979939. https://archive.org/details/bookofnumbers0000conw/page/91.
- Dobiński, G. (1877). "Summirung der Reihe für m = 1, 2, 3, 4, 5, …". Grunert's Archiv 61: 333–336. https://archive.org/stream/archivdermathem88unkngoog#page/n346.
- Engel, Konrad (1994). "On the average rank of an element in a filter of the partition lattice". Journal of Combinatorial Theory. Series A 65 (1): 67–78. doi:10.1016/0097-3165(94)90038-8.
- "II.3 Surjections, set partitions, and words". Analytic Combinatorics. Cambridge University Press. 2009. pp. 106–119.
- "The Bells: versatile numbers that can count partitions of a set, primes and even rhymes". Scientific American 238 (5): 24–30. 1978. doi:10.1038/scientificamerican0578-24. Bibcode: 1978SciAm.238e..24G. Reprinted with an addendum as "The Tinkly Temple Bells", Chapter 2 of Fractal Music, Hypercards, and more ... Mathematical Recreations from Scientific American, W. H. Freeman, 1992, pp. 24–38
- Hazewinkel, Michiel, ed. (2001), "Bell numbers", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/b110240
- Hurst, Greg; Schultz, Andrew (2009). "An elementary (number theory) proof of Touchard's congruence". arXiv:0906.0696 [math.CO].
- Knuth, Donald E. (2013). "Two thousand years of combinatorics". in Wilson, Robin; Watkins, John J.. Combinatorics: Ancient and Modern. Oxford University Press. pp. 7–37.
- Lovász, L. (1993). "Section 1.14, Problem 9". Combinatorial Problems and Exercises (2nd ed.). Amsterdam, Netherlands: North-Holland. p. 17. ISBN 9780821869475. https://books.google.com/books?id=e99fXXYx9zcC&pg=PA17.
- "An asymptotic formula for the Bell numbers". Transactions of the Royal Society of Canada, Section III 49: 49–54. 1955.
- "On the algebra of logic". American Journal of Mathematics 3 (1): 15–57. 1880. doi:10.2307/2369442..
- "The number of partitions of a set". American Mathematical Monthly 71 (5): 498–504. 1964. doi:10.2307/2312585.
- Spivey, Michael Z. (2008). "A generalized recurrence for Bell numbers". Journal of Integer Sequences 11 (2): Article 08.2.5, 3. Bibcode: 2008JIntS..11...25S. http://www.cs.uwaterloo.ca/journals/JIS/VOL11/Spivey/spivey25.pdf.
- "Aurifeuillian factorizations and the period of the Bell numbers modulo a prime". Mathematics of Computation 65 (213): 383–391. 1996. doi:10.1090/S0025-5718-96-00683-7. Bibcode: 1996MaCom..65..383W. http://homes.cerias.purdue.edu/~ssw/bell/bell.ps.
- Wilf, Herbert S. (1994). Generatingfunctionology (2nd ed.). Boston, MA: Academic Press. ISBN 0-12-751956-4. https://www.math.upenn.edu/~wilf/gfology2.pdf.
- Williams, G. T. (1945). "Numbers generated by the function eex − 1". American Mathematical Monthly 52: 323–327. doi:10.2307/2305292.
External links
- Robert Dickau. "Diagrams of Bell numbers". http://mathforum.org/advanced/robertd/bell.html.
- Weisstein, Eric W.. "Bell Number". http://mathworld.wolfram.com/BellNumber.html.
- Gottfried Helms. "Further properties & Generalization of Bell-Numbers". http://go.helms-net.de/math/binomial/04_5_SummingBellStirling.pdf.
 |
