Lie superalgebra

Short description: Algebraic structure used in theoretical physics

In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z₂‑grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry. In most of these theories, the even elements of the superalgebra correspond to bosons and odd elements to fermions (but this is not always true; for example, the BRST supersymmetry is the other way around).

Definition

Formally, a Lie superalgebra is a nonassociative Z₂-graded algebra, or superalgebra, over a commutative ring (typically R or C) whose product [·, ·], called the Lie superbracket or supercommutator, satisfies the two conditions (analogs of the usual Lie algebra axioms, with grading):

Super skew-symmetry:

[math]\displaystyle{ [x,y]=-(-1)^{|x| |y|}[y,x].\ }[/math]

The super Jacobi identity:

[math]\displaystyle{ (-1)^{|x||z|}[x, [y, z]] + (-1)^{|y||x|}[y, [z, x]] + (-1)^{|z||y|}[z, [x, y]] = 0, }[/math]

where x, y, and z are pure in the Z₂-grading. Here, |x| denotes the degree of x (either 0 or 1). The degree of [x,y] is the sum of degree of x and y modulo 2.

One also sometimes adds the axioms [math]\displaystyle{ [x,x]=0 }[/math] for |x| = 0 (if 2 is invertible this follows automatically) and [math]\displaystyle{ ''x''| = 1 (if 3 is invertible this follows automatically). When the ground ring is the integers or the Lie superalgebra is a free module, these conditions are equivalent to the condition that the [[Poincaré–Birkhoff–Witt theorem holds (and, in general, they are necessary conditions for the theorem to hold). Just as for Lie algebras, the [[Universal enveloping algebra|universal enveloping algebra]] of the Lie superalgebra can be given a [[Hopf algebra]] structure. A [[Graded Lie algebra|graded Lie algebra]] (say, graded by '''Z''' or '''N''') that is anticommutative and Jacobi in the graded sense also has a \lt math\gt Z_2 }[/math] grading (which is called "rolling up" the algebra into odd and even parts), but is not referred to as "super". See note at graded Lie algebra for discussion.

Properties

Let [math]\displaystyle{ \mathfrak g = \mathfrak g_0 \oplus \mathfrak g_1 }[/math] be a Lie superalgebra. By inspecting the Jacobi identity, one sees that there are eight cases depending on whether arguments are even or odd. These fall into four classes, indexed by the number of odd elements:

1. No odd elements. The statement is just that [math]\displaystyle{ \mathfrak g_0 }[/math] is an ordinary Lie algebra.
2. One odd element. Then [math]\displaystyle{ \mathfrak g_1 }[/math] is a [math]\displaystyle{ \mathfrak g_0 }[/math]-module for the action [math]\displaystyle{ \mathrm{ad}_a: b \rightarrow [a, b], \quad a \in \mathfrak g_0, \quad b, [a, b] \in \mathfrak g_1 }[/math].
3. Two odd elements. The Jacobi identity says that the bracket [math]\displaystyle{ \mathfrak g_1 \otimes \mathfrak g_1 \rightarrow \mathfrak g_0 }[/math] is a symmetric [math]\displaystyle{ \mathfrak g_1 }[/math]-map.
4. Three odd elements. For all [math]\displaystyle{ b \in \mathfrak g_1 }[/math], [math]\displaystyle{ [b,[b,b]] = 0 }[/math].

Thus the even subalgebra [math]\displaystyle{ \mathfrak g_0 }[/math] of a Lie superalgebra forms a (normal) Lie algebra as all the signs disappear, and the superbracket becomes a normal Lie bracket, while [math]\displaystyle{ \mathfrak g_1 }[/math] is a linear representation of [math]\displaystyle{ \mathfrak g_0 }[/math], and there exists a symmetric [math]\displaystyle{ \mathfrak g_0 }[/math]-equivariant linear map [math]\displaystyle{ \{\cdot,\cdot\}:\mathfrak g_1\otimes \mathfrak g_1\rightarrow \mathfrak g_0 }[/math] such that,

[math]\displaystyle{ [\left\{x, y\right\},z]+[\left\{y, z\right\},x]+[\left\{z, x\right\},y]=0, \quad x,y, z \in \mathfrak g_1. }[/math]

Conditions (1)–(3) are linear and can all be understood in terms of ordinary Lie algebras. Condition (4) is nonlinear, and is the most difficult one to verify when constructing a Lie superalgebra starting from an ordinary Lie algebra ([math]\displaystyle{ \mathfrak g_0 }[/math]) and a representation ([math]\displaystyle{ \mathfrak g_1 }[/math]).

Involution

A ^∗ Lie superalgebra is a complex Lie superalgebra equipped with an involutive antilinear map from itself to itself which respects the Z₂ grading and satisfies [x,y]^* = [y^*,x^*] for all x and y in the Lie superalgebra. (Some authors prefer the convention [x,y]^* = (−1)^|x||y|[y^*,x^*]; changing * to −* switches between the two conventions.) Its universal enveloping algebra would be an ordinary ^*-algebra.

Examples

Given any associative superalgebra [math]\displaystyle{ A }[/math] one can define the supercommutator on homogeneous elements by

[math]\displaystyle{ [x,y] = xy - (-1)^{|x||y|}yx\ }[/math]

and then extending by linearity to all elements. The algebra [math]\displaystyle{ A }[/math] together with the supercommutator then becomes a Lie superalgebra. The simplest example of this procedure is perhaps when [math]\displaystyle{ A }[/math] is the space of all linear functions [math]\displaystyle{ \mathbf {End}(V) }[/math] of a super vector space [math]\displaystyle{ V }[/math] to itself. When [math]\displaystyle{ V = \mathbb K^{p|q} }[/math], this space is denoted by [math]\displaystyle{ M^{p|q} }[/math] or [math]\displaystyle{ M(p|q) }[/math]. With the Lie bracket per above, the space is denoted [math]\displaystyle{ \mathfrak {gl}(p|q) }[/math].

The Whitehead product on homotopy groups gives many examples of Lie superalgebras over the integers.

The super-Poincaré algebra generates the isometries of flat superspace.

Classification

The simple complex finite-dimensional Lie superalgebras were classified by Victor Kac.

They are (excluding the Lie algebras):

The special linear lie superalgebra [math]\displaystyle{ \mathfrak{sl}(m|n) }[/math].

The lie superalgebra [math]\displaystyle{ \mathfrak{sl}(m|n) }[/math] is the subalgebra of [math]\displaystyle{ \mathfrak{gl}(m|n) }[/math] consisting of matrices with super trace zero. It is simple when [math]\displaystyle{ m\not=n }[/math]. If [math]\displaystyle{ m=n }[/math], then the identity matrix [math]\displaystyle{ I_{2m} }[/math]generates an ideal. Quotienting out this ideal leads to [math]\displaystyle{ \mathfrak{sl}(m|m) / \langle I_{2m} \rangle }[/math] which is simple for [math]\displaystyle{ m \geq 2 }[/math].

The orthosymplectic Lie superalgebra [math]\displaystyle{ \mathfrak{osp}(m|2n) }[/math].

Consider an even, non-degenerate, supersymmetric bilinear form [math]\displaystyle{ \langle \cdot, \cdot \rangle }[/math] on [math]\displaystyle{ \mathbb{C}^{m|2n} }[/math]. Then the orthosymplectic Lie superalgebra is the subalgebra of [math]\displaystyle{ \mathfrak{gl}(m|2n) }[/math] consisting of matrices that leave this form invariant:[math]\displaystyle{ \mathfrak{osp}(m|2n) = \{ X \in \mathfrak{gl}(m|2n) \mid \langle X u,v \rangle + (-1)^{|X||u|} \langle u, X v\rangle =0 \text{ for all } u,v \in \mathbb{C}^{m|2n} \}. }[/math] Its even part is given by [math]\displaystyle{ \mathfrak{so}(m) \oplus \mathfrak{sp}(2n) }[/math].

The exceptional Lie superalgebra [math]\displaystyle{ D(2,1;\alpha) }[/math].

There is a family of (9∣8)-dimensional Lie superalgebras depending on a parameter [math]\displaystyle{ \alpha }[/math]. These are deformations of [math]\displaystyle{ D(2,1)=\mathfrak{osp}(4|2) }[/math]. If [math]\displaystyle{ \alpha\not=0 }[/math] and [math]\displaystyle{ \alpha\not=-1 }[/math], then D(2,1,α) is simple. Moreover [math]\displaystyle{ D(2,1;\alpha) \cong D(2,1;\beta) }[/math] if [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are under the same orbit under the maps [math]\displaystyle{ \alpha \mapsto \alpha^{-1} }[/math] and [math]\displaystyle{ \alpha \mapsto -1-\alpha }[/math].

The exceptional Lie superalgebra [math]\displaystyle{ F(4) }[/math].

It has dimension (24|16). Its even part is given by [math]\displaystyle{ \mathfrak{sl}(2) \oplus \mathfrak{so}(7) }[/math].

The exceptional Lie superalgebra [math]\displaystyle{ G(3) }[/math].

It has dimension (17|14). Its even part is given by [math]\displaystyle{ \mathfrak{sl}(2) \oplus G_2 }[/math].

There are also two so-called strange series called [math]\displaystyle{ \mathfrak{pe}(n) }[/math] and [math]\displaystyle{ \mathfrak{q}(n) }[/math].

The Cartan types. They can be divided in four families: [math]\displaystyle{ W(n) }[/math], [math]\displaystyle{ S(n) }[/math], [math]\displaystyle{ \widetilde{S}(2n) }[/math] and [math]\displaystyle{ H(n) }[/math]. For the Cartan type of simple Lie superalgebras, the odd part is no longer completely reducible under the action of the even part.

Classification of infinite-dimensional simple linearly compact Lie superalgebras

The classification consists of the 10 series W(m, n), S(m, n) ((m, n) ≠ (1, 1)), H(2m, n), K(2m + 1, n), HO(m, m) (m ≥ 2), SHO(m, m) (m ≥ 3), KO(m, m + 1), SKO(m, m + 1; β) (m ≥ 2), SHO ∼ (2m, 2m), SKO ∼ (2m + 1, 2m + 3) and the five exceptional algebras:

E(1, 6), E(5, 10), E(4, 4), E(3, 6), E(3, 8)

The last two are particularly interesting (according to Kac) because they have the standard model gauge group SU(3)×SU(2)×U(1) as their zero level algebra. Infinite-dimensional (affine) Lie superalgebras are important symmetries in superstring theory. Specifically, the Virasoro algebras with [math]\displaystyle{ \mathcal{N} }[/math] supersymmetries are [math]\displaystyle{ K(1, \mathcal{N}) }[/math] which only have central extensions up to [math]\displaystyle{ \mathcal{N} = 4 }[/math].

Category-theoretic definition

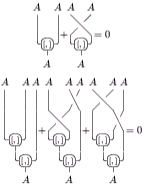
In category theory, a Lie superalgebra can be defined as a nonassociative superalgebra whose product satisfies

• [math]\displaystyle{ [\cdot,\cdot]\circ ({\operatorname{id}}+\tau_{A,A})=0 }[/math]
• [math]\displaystyle{ [\cdot,\cdot]\circ ([\cdot,\cdot]\otimes {\operatorname{id}} \circ({\operatorname{id}}+\sigma+\sigma^2)=0 }[/math]

where σ is the cyclic permutation braiding [math]\displaystyle{ ({\operatorname{id}} \otimes\tau_{A,A}) \circ (\tau_{A,A}\otimes {\operatorname{id}}) }[/math]. In diagrammatic form:

See also

• Gerstenhaber algebra
• Anyonic Lie algebra
• Grassmann algebra
• Representation of a Lie superalgebra
• Superspace
• Supergroup
• Universal enveloping algebra

References

• Cheng, S.-J.; Wang, W. (2012). Dualities and Representations of Lie Superalgebras. Graduate Studies in Mathematics. 144. pp. 302pp. ISBN 978-0-8218-9118-6. 
• Freund, P. G. O. (1983). Introduction to supersymmetry. Cambridge Monographs on Mathematical Physics. Cambridge University Press. doi:10.1017/CBO9780511564017. ISBN 978-0521-356-756. 
• Grozman, P.; Leites, D.; Shchepochkina, I. (2005). "Lie Superalgebras of String Theories". Acta Mathematica Vietnamica 26 (2005): 27–63. Bibcode: 1997hep.th....2120G. 
• Kac, V. G. (1977). "Lie superalgebras". Advances in Mathematics 26 (1): 8–96. doi:10.1016/0001-8708(77)90017-2. 
• Kac, V. G. (2010). "Classification of Infinite-Dimensional Simple Groups of Supersymmetries and Quantum Field Theory". Visions in Mathematics. pp. 162–183. doi:10.1007/978-3-0346-0422-2_6. ISBN 978-3-0346-0421-5. 
• Manin, Y. I. (1997). Gauge Field Theory and Complex Geometry ((2nd ed.) ed.). Berlin: Springer. ISBN 978-3-540-61378-7. 
• Musson, I. M. (2012). Lie Superalgebras and Enveloping Algebras. Graduate Studies in Mathematics. 131. pp. 488 pp. ISBN 978-0-8218-6867-6. https://www.ams.org/bookstore?fn=20&arg1=tb-aa&ikey=GSM-131. 
• Varadarajan, V. S. (2004). Supersymmetry for Mathematicians: An Introduction. Courant Lecture Notes in Mathematics. 11. American Mathematical Society. ISBN 978-0-8218-3574-6. https://books.google.com/books?id=sZ1-G4hQgIIC&q=supersymmetry+for+mathematicians&pg=PA1. 

Historical

• Frölicher, A.; Nijenhuis, A. (1956). "Theory of vector valued differential forms. Part I". Indagationes Mathematicae 59: 338–350. doi:10.1016/S1385-7258(56)50046-7. .
• Gerstenhaber, M. (1963). "The cohomology structure of an associative ring". Annals of Mathematics 78 (2): 267–288. doi:10.2307/1970343. 
• Gerstenhaber, M. (1964). "On the Deformation of Rings and Algebras". Annals of Mathematics 79 (1): 59–103. doi:10.2307/1970484. 
• Milnor, J. W.; Moore, J. C. (1965). "On the structure of Hopf algebras". Annals of Mathematics 81 (2): 211–264. doi:10.2307/1970615. https://polipapers.upv.es/index.php/AGT/article/view/2250. 

External links

• Irving Kaplansky + Lie Superalgebras