Pattern search (optimization)

Example of convergence of a direct search method on the Broyden function. At each iteration, the pattern either moves to the point which best minimizes its objective function, or shrinks in size if no point is better than the current point, until the desired accuracy has been achieved, or the algorithm reaches a predetermined number of iterations.

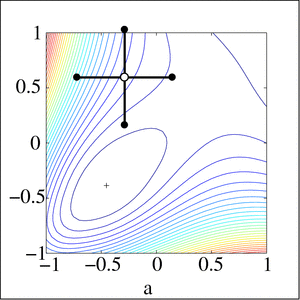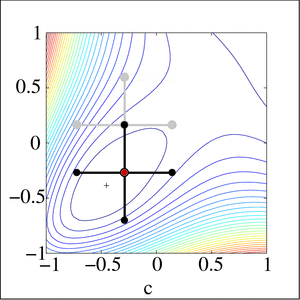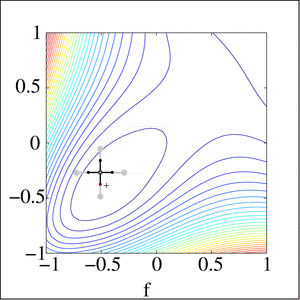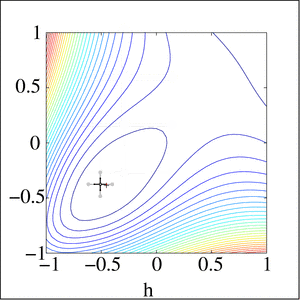
Pattern search (also known as direct search, derivative-free search, or black-box search) is a family of numerical optimization methods that does not require a gradient. As a result, it can be used on functions that are not continuous or differentiable. One such pattern search method is "convergence" (see below), which is based on the theory of positive bases. Optimization attempts to find the best match (the solution that has the lowest error value) in a multidimensional analysis space of possibilities.

History

The name "pattern search" was coined by Hooke and Jeeves. An early and simple variant is attributed to Fermi and Metropolis when they worked at the Los Alamos National Laboratory. It is described by Davidon, as follows:

They varied one theoretical parameter at a time by steps of the same magnitude, and when no such increase or decrease in any one parameter further improved the fit to the experimental data, they halved the step size and repeated the process until the steps were deemed sufficiently small.

Convergence

Convergence is a pattern search method proposed by Yu, who proved that it converges using the theory of positive bases. Later, Torczon, Lagarias and co-authors used positive-basis techniques to prove the convergence of another pattern-search method on specific classes of functions. Outside of such classes, pattern search is a heuristic that can provide useful approximate solutions for some issues, but can fail on others. Outside of such classes, pattern search is not an iterative method that converges to a solution; indeed, pattern-search methods can converge to non-stationary points on some relatively tame problems.

See also

• Golden-section search conceptually resembles PS in its narrowing of the search range, only for single-dimensional search spaces.
• Nelder–Mead method aka. the simplex method conceptually resembles PS in its narrowing of the search range for multi-dimensional search spaces but does so by maintaining n + 1 points for n-dimensional search spaces, whereas PS methods computes 2n + 1 points (the central point and 2 points in each dimension).
• Luus–Jaakola samples from a uniform distribution surrounding the current position and uses a simple formula for exponentially decreasing the sampling range.
• Random search is a related family of optimization methods that sample from a hypersphere surrounding the current position.
• Random optimization is a related family of optimization methods that sample from a normal distribution surrounding the current position.