Philosophy:Affirming the consequent

Short description: Type of fallacious argument (logical fallacy)

Affirming the consequent, sometimes called converse error, fallacy of the converse, or confusion of necessity and sufficiency, is a formal fallacy of taking a true conditional statement (e.g., "If the lamp were broken, then the room would be dark"), and invalidly inferring its converse ("The room is dark, so the lamp is broken"), even though that statement may not be true. This arises when a consequent ("the room would be dark") has other possible antecedents (for example, "the lamp is in working order, but is switched off" or "there is no lamp in the room").

Converse errors are common in everyday thinking and communication and can result from, among other causes, communication issues, misconceptions about logic, and failure to consider other causes.

The opposite statement, denying the consequent, is a valid form of argument (modus tollens).

Formal description

There are four possible forms of hypothetical syllogisms, two of which are valid, while two of which are invalid. Considering a very simple example may help you understand why these forms are valid or invalid. If "p" represents "Candiru is a fish" and "q" represents "Candiru has gills," try to convince yourself by replacing these statements with p and q in the above table.

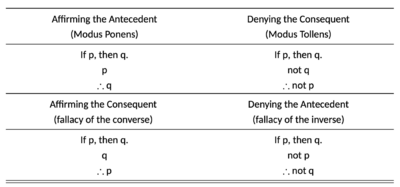
Affirming the consequent is the action of taking a true statement [math]\displaystyle{ P \to Q }[/math] and invalidly concluding its converse [math]\displaystyle{ Q \to P }[/math]. The name affirming the consequent derives from using the consequent, Q, of [math]\displaystyle{ P \to Q }[/math], to conclude the antecedent P. This fallacy can be summarized formally as [math]\displaystyle{ (P \to Q, Q)\to P }[/math] or, alternatively, [math]\displaystyle{ \frac{P \to Q, Q}{\therefore P} }[/math]. The root cause of such a logical error is sometimes failure to realize that just because P is a possible condition for Q, P may not be the only condition for Q, i.e. Q may follow from another condition as well.

Affirming the consequent can also result from overgeneralizing the experience of many statements having true converses. If P and Q are "equivalent" statements, i.e. [math]\displaystyle{ P \leftrightarrow Q }[/math], it is possible to infer P under the condition Q. For example, the statements "It is August 13, so it is my birthday" [math]\displaystyle{ P \to Q }[/math] and "It is my birthday, so it is August 13" [math]\displaystyle{ Q \to P }[/math] are equivalent and both true consequences of the statement "August 13 is my birthday" (an abbreviated form of [math]\displaystyle{ P \leftrightarrow Q }[/math]).

Of the possible forms of "mixed hypothetical syllogisms," two are valid and two are invalid. Affirming the antecedent (modus ponens) and denying the consequent (modus tollens) are valid. Affirming the consequent and denying the antecedent are invalid(see table).

Additional examples

Example 1

One way to demonstrate the invalidity of this argument form is with a counterexample with true premises but an obviously false conclusion. For example:

If someone lives in San Diego, then they live in California .

Joe lives in California.

Therefore, Joe lives in San Diego.

There are many ways to live in California without living in San Diego, as long as they live in a Californian place other than San Diego.

However, one can affirm with certainty that "if someone does not live in California" (non-Q), then "this person does not live in San Diego" (non-P). This is the contrapositive of the first statement, and it must be true if and only if the original statement is true.

Example 2

Here is another useful, obviously fallacious example.

If an animal is a dog, then it has four legs.

My cat has four legs.

Therefore, my cat is a dog.

Here, it is immediately intuitive that any number of other antecedents ("If an animal is a deer...", "If an animal is an elephant...", "If an animal is a moose...", etc.) can give rise to the consequent ("then it has four legs"), and that it is preposterous to suppose that having four legs must imply that the animal is a dog and nothing else. This is useful as a teaching example since most people can immediately recognize that the conclusion reached must be wrong (intuitively, a cat cannot be a dog), and that the method by which it was reached must therefore be fallacious.

Example 3

Arguments of the same form can sometimes seem superficially convincing, as in the following example:

If Brian had been thrown off the top of the Eiffel Tower, then he would be dead.

Brian is dead.

Therefore, Brian was thrown off the top of the Eiffel Tower.

Being thrown off the top of the Eiffel Tower is not the only cause of death, since there exist numerous different causes of death.

Example 4

In Catch-22, the chaplain is interrogated for supposedly being "Washington Irving"/"Irving Washington", who has been blocking out large portions of soldiers' letters home. The colonel has found such a letter, but with the Chaplain's name signed.

"You can read, though, can't you?" the colonel persevered sarcastically. "The author signed his name."

"That's my name there."

"Then you wrote it. Q.E.D."

P in this case is 'The chaplain signs his own name', and Q 'The chaplain's name is written'. The chaplain's name may be written, but he did not necessarily write it, as the colonel falsely concludes.

Example 5

When teaching the scientific method, the following example is used to illustrate why, via the fallacy of affirming the consequent, no scientific theory is ever proven true but rather simply failed to be falsified.

If this theory is correct, we will observe X.

We observe X.

Therefore, this theory is correct.

Concluding or assuming that a theory is true because of a prediction it makes being observed is invalid. This is one of the challenges of applying the scientific method though rarely is it brought up in academic contexts as it is unlikely to be of consequence to the results of the study. Much more common is questioning the validity of the theory, the validity of expected the theory to have predicted the observation, and/or the validity of the observation itself.

See also

• Abductive reasoning
• Appeal to consequences
• Confusion of the inverse
• Denying the antecedent
• Fallacy of the single cause
• Fallacy of the undistributed middle
• Modus ponens
• Necessity and sufficiency