Physics:Addressed fiber Bragg structure

Short description: Optical frequency response of which includes two narrowband components

An addressed fiber Bragg structure (AFBS) is a fiber Bragg grating, the optical frequency response of which includes two narrowband components with the frequency spacing between them (which is the address frequency of the AFBS) being in the radio frequency (RF) range. The frequency spacing (the address frequency) is unique for every AFBS in the interrogation circuit and does not change when the AFBS is subjected to strain or temperature variation. An addressed fiber Bragg structure can perform triple function in fiber-optic sensor systems: a sensor, a shaper of double-frequency probing radiation, and a multiplexor. The key feature of AFBS is that it enables the definition of its central wavelength without scanning its spectral response, as opposed to conventional fiber Bragg gratings (FBG), which are probed using optoelectronic interrogators. An interrogation circuit of AFBS is significantly simplified in comparison with conventional interrogators and consists of a broadband optical source (such as a superluminescent diode), an optical filter with a predefined linear inclined frequency response, and a photodetector. The AFBS interrogation principle intrinsically allows to include several AFBSs with the same central wavelength and different address frequencies into a single measurement system.

Figure 1: A schematic of a refractive index change of a 2π-FBG-type addressed fiber Bragg structure (a), its spectral response (b). λ_B is the central (Bragg) wavelength, Ω is the address frequency, S₁(λ) - S₃(λ) denote transfer matrixes describing the uniform sections of the AFBS, S_φ(λ) denotes transfer matrix describing the phase-shift section of the AFBS.

History

The concept of addressed fiber Bragg structures was introduced in 2018 by Airat Sakhabutdinov and developed in collaboration with his scientific adviser, Oleg Morozov. The idea emerged from the earlier works of Morozov and his colleagues, where the double-frequency optical radiation from an electro-optic modulator was used for the definition of the FBG central wavelength based on the amplitude and phase analysis of the beating signal at the frequency equal to the spacing between the two components of the probing radiation. This eliminates the need for scanning the FBG spectral response while providing high accuracy of measurements and reducing the system cost. AFBS has been developed as a further step towards simplification of FBG interrogation systems by transferring the shaping of double-frequency probing radiation from the source modulator to the sensor itself.

Types of AFBS

Thus far, two types of AFBS with different mechanisms of forming double-frequency radiation have been presented: 2π-FBG and 2λ-FBG.

2π-FBG

A 2π-FBG is an FBG with two discrete phase π-shifts. It comprises three sequential uniform FBGs with gaps equal to one grating period between them (see Fig. 1). In the system, several 2π-FBGs must be connected in parallel so that the photodetector receives the light propagated through the structures.

2λ-FBG

A 2λ-FBG consists of two identical ultra-narrow FBGs, the central wavelengths of which are separated by an address frequency. Several 2λ-FBGs in the system can be connected in series, so that the photodetector receives the light reflected from the structures.

Interrogation principle

Figure 2: An interrogation scheme for two addressed fiber Bragg structures (2π-FBG-type): 1 - a wideband optical source; 2.1 and 2.2 - addressed fiber Bragg structures; 3 - an optical filter with a pre-defined linear inclined frequency response; 4, 7 - photodetectors; 5, 8 - analog-to digital converters; 6, 9 - fiber-optic splitters; 10 - fiber-optic coupler; a - e - optical spectra.

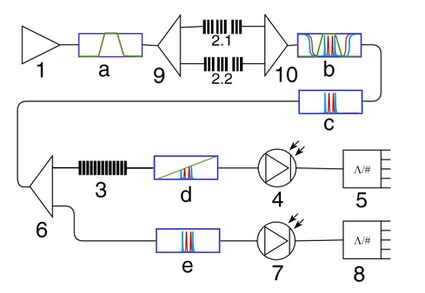
Fig. 2 presents the block diagram of the interrogation system for two AFBSs (2π-FBG-type) with different address frequencies Ω₁ and Ω₂. A broadband light source 1 generates continuous light radiation (diagram a), which corresponds to the measurement bandwidth. The light is transmitted through the fiber-optic coupler 9, then enters the two AFBSs 2.1 and 2.2. Both AFBSs transmit two-frequency radiations that are summed into a combined radiation (diagram b) using another coupler 10. At the output of the coupler, a four-frequency radiation (diagram c) is formed, which is sent through a fiber-optic splitter 6. The splitter divides the optical signal into two channels – the measuring channel and the reference channel. In the measuring channel, an optical filter 3 with a pre-defined linear inclined frequency response is installed, which modifies the amplitudes of the four-frequency radiation into the asymmetrical radiation (diagram d). After that, the signal is sent to the photodetector 4 and is received by the measuring analog-to-digital converter (ADC) 5. The signal from the ADC is used to define the measurement information from the AFBS. In the reference channel, the signal (diagram e) is sent to the reference photodetector 7 for the optical power output control, and then it is received by the reference ADC 8. Thus, the normalization of output signal intensity is achieved, and all subsequent calculations are performed using the relations of the intensities in the measuring and reference channels.

Assume that the response from each spectral components of AFBSs is represented by a single harmonic, then the total optical response from the two AFBSs can be expressed as:

[math]\displaystyle{ F(t)=\left[{\sum_{i=1}^NA_i\sin(\omega_it)+B_i\sin((\omega_i+\Omega_i)t)}\right]^2, }[/math]

where A_i, B_i are the amplitudes of the frequency components of the i-th AFBS; ω_i, is the frequency of the left spectral components of the i-th AFBS; Ω_i is the address frequency of the i-th AFBS.

The luminous power received by the photodetector can be described by the following expression:

[math]\displaystyle{ P(t)=\sum_{i=1}^N\sum_{k=1}^N\left({A_iA_k\cos((\omega_i-\omega_k)t)+A_iB_k\cos((\omega_i-\omega_k-\Omega_k)t)+ \atop B_iA_k\cos((\omega_i-\omega_k+\Omega_i)t)+B_iB_k\cos((\omega_i-\omega_k+\Omega_i-\Omega_k)t)}\right). }[/math]

By narrowband filtering of the signal P(t) at the address frequencies, a system of equations can be obtained, using which the central frequencies of the AFBSs can be defined:

[math]\displaystyle{ \sum_{i=1}^N\sum_{k=1}^N\left({A_iA_k\exp\left ( -\frac{(\Omega_j-|\omega_i-\omega_k|)^2}{2\sigma^2} \right )+A_iB_k\exp\left ( -\frac{(\Omega_j-|\omega_i-\omega_k-\Omega_k|)^2}{2\sigma^2} \right )+ \atop B_iA_k\exp\left ( -\frac{(\Omega_j-|\omega_i-\omega_k+\Omega_i|)^2}{2\sigma^2} \right )+B_iB_k\exp\left ( -\frac{(\Omega_j-|\omega_i-\omega_k+\Omega_i-\Omega_k|)^2}{2\sigma^2} \right )}\right)=D_j, j=\overline{1,N}, }[/math]

where D_j is the amplitude of the signal at the address frequencies Ω_j, and the exponential multipliers describe the bandpass filters at the address frequencies.