Physics:Balance of angular momentum

Playground merry-go-round

The balance of angular momentum or Euler's second law in classical mechanics is a law of physics, stating that to alter the angular momentum of a body a torque must be applied to it.

An example of use is the playground merry-go-round in the picture. To put it in rotation it must be pushed. Technically one summons a torque that feeds angular momentum to the merry-go-round. The torque of frictional forces in the bearing and drag, however, make a resistive torque that will gradually lessen the angular momentum and eventually stop rotation.

The mathematical formulation states that the rate of change [math]\displaystyle{ \dot{\vec L}_c }[/math] of angular momentum [math]\displaystyle{ \vec L_c }[/math] about a point [math]\displaystyle{ \vec c }[/math], is equal to the sum of the external torques [math]\displaystyle{ \vec M_c }[/math] acting on that body about that point:

[math]\displaystyle{ \vec M_c = \dot{\vec L}_c }[/math]

The point [math]\displaystyle{ \vec c }[/math] is a fixed point in an inertial system or the center of mass of the body. In the special case, when external torques vanish, it shows that the angular momentum is preserved. The d'Alembert force counteracting the change of angular momentum shows as a gyroscopic effect.

From the balance of angular momentum follows the equality of corresponding shear stresses or the symmetry of the Cauchy stress tensor. The same follows from the Boltzmann Axiom, according to which internal forces in a continuum are torque-free. Thus the balance of angular momentum, the symmetry of the Cauchy stress tensor, and the Boltzmann Axiom in continuum mechanics are related terms.

Especially in the theory of the top the balance of angular momentum plays a crucial part. In continuum mechanics it serves to exactly determine the skew-symmetric part of the stress tensor.

The balance of angular momentum is, besides the Newtonian laws, a fundamental and independent principle and was introduced as such first by Swiss mathematician and physicist Leonhard Euler in 1775.

History

Swiss mathematician Jakob I Bernoulli applied the balance of angular momentum in 1703 – without explicitly formulating it – to find the center of oscillation of a pendulum, which he had already done in a first, somewhat incorrect manner in 1686. The balance of angular momentum thus preceded Newton's laws, which were first published in 1687.

In 1744, Euler was the first to use the principles of momentum and of angular momentum to state the equations of motion of a system. In 1750, in his treatise "Discovery of a new principle of mechanics" he published the Euler's equations of rigid body dynamics, which today are derived from the balance of angular momentum, which Euler, however, could deduce for the rigid body from Newton's second law. After studies on plane elastic continua, which are indispensable to the balance of the torques, Euler raised the balance of angular momentum to an independent principle for calculation of the movement of bodies in 1775.

In 1822, French mathematician Augustin-Louis Cauchy introduced the stress tensor whose symmetry in combination with the balance of linear momentum made sure the fulfillment of the balance of angular momentum in the general case of the deformable body. The interpretation [math]\displaystyle{ \vec M=\dot{\vec L} }[/math] of the balance of angular momentum was first noted by M. P. Saint-Guilhem in 1851.

Kinetics of rotation

Kinetics deals with states that are not in mechanical equilibrium. According to Newton's second law, an external force leads to a change in velocity (acceleration) of a body. Analogously an external torque means a change in angular velocity resulting in an angular acceleration. The inertia relating to rotation depends not only on the mass of a body but also on its spatial distribution. With a rigid body this is expressed by the moment of inertia. With a rotation around a fixed axis, the torque is proportional to the angular acceleration with the moment of inertia as proportionality factor. Here it is to be noted that the moment of inertia is not only dependent on the position of the axis of rotation (see Steiner Theorem) but also on its direction. Should the above law be formulated more generally for any axis of rotation then the inertia tensor must be used.

With the two-dimensional special case, a torque only results in an acceleration or slowing down of a rotation. With the general three-dimensional case, however, it can also alter the direction of the axis (precession).

Formulations

• In rigid body dynamics the balance of angular momentum leads to Euler's equations.
• In continuum mechanics the balance of angular momentum leads to Cauchy's second law of motion, that states the symmetry of the Cauchy stress tensor. The Boltzmann Axiom has the same consequence.

Boltzmann Axiom

Stresses on a volume element (blue) with width dx and height dy (not displayed)

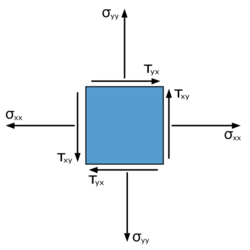
In 1905, Austrian physicist Ludwig Boltzmann pointed out that with reduction of a body into infinitesimally smaller volume elements, the inner reactions have to meet all static conditions for mechanical equilibrium. Cauchy's stress theorem handles the equilibrium in terms of force. For the analogous statement in terms of torque, German mathematician Georg Hamel coined the name Boltzmann Axiom.

This axiom is equivalent to the symmetry of the Cauchy stress tensor. For the resultants of the stresses do not exert a torque on the volume element, the resultant force must lead through the center of the volume element. The line of action of the inertia forces and the normal stress resultants σ_xx·dy and σ_yy·dx lead through the center of the volume element. In order that the shear stress resultants τ_xy·dy and τ_yx·dx lead through the center of the volume element

[math]\displaystyle{ \frac{\tau_{xy}\mathrm{d}y}{\tau_{yx}\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}x} \quad\rightarrow\quad\tau_{yx}=\tau_{xy} }[/math]

must hold. This is actually the statement of the equality of corresponding shear stresses in the xy plane.

Cosserat Continuum

In addition to the torque-free classical continuum with a symmetric stress tensor, cosserat continua (polar continua) that are not torque-free have also been defined. One application of such a continuum is the theory of shells. Cosserat continua are not only capable to transport a momentum flux but also an angular momentum flux. Therefore, there also may be sources of momentum and angular momentum inside the body. Here the Boltzmann Axiom does not apply and the stress tensor may be skew-symmetric.

If these fluxes are treated as usual in continuum mechanics, field equations arise in which the skew-symmetric part of the stress tensor has no energetic significance. The balance of angular momentum becomes independent of the balance of energy and is used to determine the skew-symmetric part of the stress tensor. American mathematician Clifford Truesdell saw in this the "true basic sense of Euler's second law".

Area rule

The area (olive green) swept by the driving beam [math]\displaystyle{ \vec r(t) }[/math] (AB→AC) changes into a triangle when Δt becomes infinitesimally small

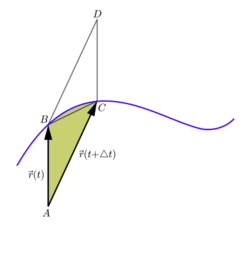
The area rule is a corollary of the angular momentum law in the form: The resulting moment is equal to the product of twice the mass and the time derivative of the areal velocity.

It refers to the ray [math]\displaystyle{ \vec r }[/math] to a point mass with mass m. This has the angular momentum with the velocity [math]\displaystyle{ \dot{\vec r} }[/math] and the momentum [math]\displaystyle{ \vec p=m\dot{\vec r} }[/math]

[math]\displaystyle{ \vec L=\vec r\times\vec p=m\vec r\times\dot{\vec r} =m\vec r\times\mathrm{d}\vec r/\mathrm{d}t }[/math].

In the infinitesimal time dt the trajectory sweeps over a triangle whose content is [math]\displaystyle{ \mathrm{d}\vec A=\tfrac12\vec r\times\mathrm{d}\vec r }[/math], see image, areal velocity and cross product "×". This is how it turns out:

[math]\displaystyle{ \vec L=m\vec r\times\mathrm{d}\vec r/\mathrm{d}t =2m\,\mathrm{d}\vec A/\mathrm{d}t=2m\dot{\vec A} }[/math].

With Euler's second law this becomes:

[math]\displaystyle{ \vec M=\dot{\vec L}=2m\ddot{\vec A} }[/math].

The special case of plane, moment-free central force motion is treated by Kepler's second law, also known as the area rule.