Physics:Bessel beam

From HandWiki
Short description: Non-diffractive wave
Evolution of a Bessel beam.
Diagram of axicon and resulting Bessel beam
Cross-section of the Bessel beam and graph of intensity
Bessel beam re-forming central bright area after obstruction

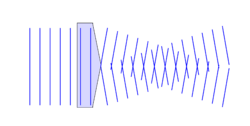
A Bessel beam is a wave whose amplitude is described by a Bessel function of the first kind.[1][2][3] Electromagnetic, acoustic, gravitational, and matter waves can all be in the form of Bessel beams. A true Bessel beam is non-diffractive. This means that as it propagates, it does not diffract and spread out; this is in contrast to the usual behavior of light (or sound), which spreads out after being focused down to a small spot. Bessel beams are also self-healing, meaning that the beam can be partially obstructed at one point, but will re-form at a point further down the beam axis.

As with a plane wave, a true Bessel beam cannot be created, as it is unbounded and would require an infinite amount of energy. Reasonably good approximations can be made,[4] however, and these are important in many optical applications because they exhibit little or no diffraction over a limited distance. Approximations to Bessel beams are made in practice either by focusing a Gaussian beam with an axicon lens to generate a Bessel–Gauss beam, by using axisymmetric diffraction gratings,[5] or by placing a narrow annular aperture in the far field.[3] High order Bessel beams can be generated by spiral diffraction gratings.[6]

Properties

The properties of Bessel beams[7][8] make them extremely useful for optical tweezing, as a narrow Bessel beam will maintain its required property of tight focus over a relatively long section of beam and even when partially occluded by the dielectric particles being tweezed. Similarly, particle manipulation with acoustical tweezers was achieved[9][10] with a Bessel beam that scatters[11][12][13][14] and produces a radiation force resulting from the exchange of acoustic momentum between the wave-field and a particle placed along its path.[15][16][17][18][19][20][21][22][23]

The mathematical function which describes a Bessel beam is a solution of Bessel's differential equation, which itself arises from separable solutions to Laplace's equation and the Helmholtz equation in cylindrical coordinates. The fundamental zero-order Bessel beam has an amplitude maximum at the origin, while a high-order Bessel beam (HOBB) has an axial phase singularity along the beam axis; the amplitude is zero there. HOBBs can be of vortex (helicoidal) or non-vortex types.[24]

X-waves are special superpositions of Bessel beams which travel at constant velocity, and can exceed the speed of light.[25]

Mathieu beams and parabolic (Weber) beams[26] are other types of non-diffractive beams that have the same non-diffractive and self-healing properties of Bessel beams but different transverse structures.

Acceleration

In 2012 it was theoretically proven[27] and experimentally demonstrated[28] that, with a special manipulation of their initial phase, Bessel beams can be made to accelerate along arbitrary trajectories in free space. These beams can be considered as hybrids that combine the symmetric profile of a standard Bessel beam with the self-acceleration property of the Airy beam and its counterparts. Previous efforts to produce accelerating Bessel beams included beams with helical[29] and sinusoidal[30] trajectories as well as the early effort for beams with piecewise straight trajectories.[31]

Attenuation-compensation

Beams may encounter losses as they travel through materials which will cause attenuation of the beam intensity. A property common to non-diffracting (or propagation-invariant) beams, such as the Airy beam and Bessel beam, is the ability to control the longitudinal intensity envelope of the beam without significantly altering the other characteristics of the beam. This can be used to create Bessel beams which grow in intensity as they travel and can be used to counteract losses, therefore maintaining a beam of constant intensity as it propagates.[32][33]

Applications

Imaging and microscopy

In light-sheet fluorescence microscopy, non-diffracting (or propagation-invariant) beams have been utilised to produce very long and uniform light-sheets which do not change size significantly across their length. The self-healing property of Bessel beams has also shown to give improved image quality at depth as the beam shape is less distorted after travelling through scattering tissue than a Gaussian beam. Bessel beam based light-sheet microscopy was first demonstrated in 2010[34] but many variations have followed since. In 2018, it was shown that the use of attenuation-compensation could be applied to Bessel beam based light-sheet microscopy and could enable imaging at greater depths within biological specimens.[35]

Acoustofluidics

Bessel beams are a good candidate for the selectively trapping because of the concentric circles of pressure maximum and minimum in the transverse planes.

References

  1. ↑ Garcés-Chávez, V.; McGloin, D.; Melville, H.; Sibbett, W.; Dholakia, K. (2002). "Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam". Nature 419 (6903): 145–7. doi:10.1038/nature01007. PMID 12226659. Bibcode: 2002Natur.419..145G. 
  2. ↑ McGloin, D.; Dholakia, K. (2005). "Bessel beams: diffraction in a new light". Contemporary Physics 46 (1): 15–28. doi:10.1080/0010751042000275259. Bibcode: 2005ConPh..46...15M. 
  3. ↑ 3.0 3.1 Durnin, J. (1987). "Diffraction-free beams". Physical Review Letters 58 (15): 1499–1501. doi:10.1103/PhysRevLett.58.1499. PMID 10034453. Bibcode: 1987PhRvL..58.1499D. 
  4. ↑ Cox, A.J.; D'Anna, Joseph (1992). "Constant-axial-intensity nondiffracting beam". Optics Letters 17 (4): 232–234. doi:10.1364/OL.17.000232. PMID 19784285. Bibcode: 1992OptL...17..232C. 
  5. ↑ Jiménez, N. (2014). "Acoustic Bessel-like beam formation by an axisymmetric grating". Europhysics Letters 106 (2): 24005. doi:10.1209/0295-5075/106/24005. Bibcode: 2014EL....10624005J. 
  6. ↑ Jiménez, N. (2016). "Formation of high-order acoustic Bessel beams by spiral diffraction gratings". Physical Review E 94 (5): 053004. doi:10.1103/PhysRevE.94.053004. PMID 27967159. Bibcode: 2016PhRvE..94e3004J. 
  7. ↑ Fahrbach, F. O.; Simon, P.; Rohrbach, A. (2010). "Microscopy with self-reconstructing beams". Nature Photonics 4 (11): 780–785. doi:10.1038/nphoton.2010.204. Bibcode: 2010NaPho...4..780F. https://www.freidok.uni-freiburg.de/dnb/download/8979. 
  8. ↑ Mitri, F. G. (2011). "Arbitrary scattering of an electromagnetic zero-order Bessel beam by a dielectric sphere". Optics Letters 36 (5): 766–8. doi:10.1364/OL.36.000766. PMID 21368976. Bibcode: 2011OptL...36..766M. https://zenodo.org/record/1235664. 
  9. ↑ Hill, M. (2016). "Viewpoint: A One-Sided View of Acoustic Traps". Physics 9 (3): 3. doi:10.1103/Physics.9.3. 
  10. ↑ D. Baresch, J.L. Thomas, and R. Marchiano, Physical review letters, 2016, 116(2), 024301.
  11. ↑ Marston, P. L. (2007). "Scattering of a Bessel beam by a sphere". The Journal of the Acoustical Society of America 121 (2): 753–758. doi:10.1121/1.2404931. PMID 17348499. Bibcode: 2007ASAJ..121..753M. 
  12. ↑ Silva, G. T. (2011). "Off-axis scattering of an ultrasound bessel beam by a sphere". IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control 58 (2): 298–304. doi:10.1109/TUFFC.2011.1807. PMID 21342815. 
  13. ↑ Mitri, F. G.; Silva, G. T. (2011). "Off-axial acoustic scattering of a high-order Bessel vortex beam by a rigid sphere". Wave Motion 48 (5): 392–400. doi:10.1016/j.wavemoti.2011.02.001. https://zenodo.org/record/1259453. 
  14. ↑ Gong, Z.; Marston, P. L.; Li, W.; Chai, Y. (2017). "Multipole expansion of acoustical Bessel beams with arbitrary order and location". The Journal of the Acoustical Society of America 141 (6): EL574–EL578. doi:10.1121/1.4985586. PMID 28679251. Bibcode: 2017ASAJ..141L.574G. 
  15. ↑ Mitri, F. G. (2008). "Acoustic radiation force on a sphere in standing and quasi-standing zero-order Bessel beam tweezers". Annals of Physics 323 (7): 1604–1620. doi:10.1016/j.aop.2008.01.011. Bibcode: 2008AnPhy.323.1604M. 
  16. ↑ Mitri, F. G.; Fellah, Z. E. A. (2008). "Theory of the acoustic radiation force exerted on a sphere by standing and quasistanding zero-order Bessel beam tweezers of variable half-cone angles". IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control 55 (11): 2469–2478. doi:10.1109/TUFFC.954. PMID 19049926. 
  17. ↑ Mitri, F. G. (2009). "Langevin acoustic radiation force of a high-order bessel beam on a rigid sphere". IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control 56 (5): 1059–1064. doi:10.1109/TUFFC.2009.1139. PMID 19473924. 
  18. ↑ Mitri, F. G. (2009). "Acoustic radiation force on an air bubble and soft fluid spheres in ideal liquids: Example of a high-order Bessel beam of quasi-standing waves". The European Physical Journal E 28 (4): 469–478. doi:10.1140/epje/i2009-10449-y. PMID 19408023. Bibcode: 2009EPJE...28..469M. 
  19. ↑ Mitri, F. G. (2009). "Negative axial radiation force on a fluid and elastic spheres illuminated by a high-order Bessel beam of progressive waves". Journal of Physics A 42 (24): 245202. doi:10.1088/1751-8113/42/24/245202. Bibcode: 2009JPhA...42x5202M. 
  20. ↑ Mitri, F. G. (2008). "Acoustic scattering of a high-order Bessel beam by an elastic sphere". Annals of Physics 323 (11): 2840–2850. doi:10.1016/j.aop.2008.06.008. Bibcode: 2008AnPhy.323.2840M. 
  21. ↑ Mitri, F. G. (2009). "Equivalence of expressions for the acoustic scattering of a progressive high-order bessel beam by an elastic sphere". IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control 56 (5): 1100–1103. doi:10.1109/TUFFC.2009.1143. PMID 19473927. 
  22. ↑ Marston, P. L. (2006). "Axial radiation force of a Bessel beam on a sphere and direction reversal of the force". The Journal of the Acoustical Society of America 120 (6): 3518–3524. doi:10.1121/1.2361185. PMID 17225382. Bibcode: 2006ASAJ..120.3518M. 
  23. ↑ Marston, P. L. (2009). "Radiation force of a helicoidal Bessel beam on a sphere". The Journal of the Acoustical Society of America 125 (6): 3539–3547. doi:10.1121/1.3119625. PMID 19507935. Bibcode: 2009ASAJ..125.3539M. 
  24. ↑ Mitri, F. G. (2011). "Linear axial scattering of an acoustical high-order Bessel trigonometric beam by compressible soft fluid spheres". Journal of Applied Physics 109 (1): 014916–014916–5. doi:10.1063/1.3518496. Bibcode: 2011JAP...109a4916M. https://zenodo.org/record/1232912. 
  25. ↑ Bowlan, P. (2009). "Measurement of the Spatiotemporal Electric Field of Ultrashort Superluminal Bessel-X Pulses". Optics and Photonics News 20 (12): 42. doi:10.1364/OPN.20.12.000042. Bibcode: 2009OptPN..20...42M. 
  26. ↑ Bandres, M. A.; Gutiérrez-Vega, J. C.; Chávez-Cerda, S. (2004). "Parabolic nondiffracting optical wave fields". Optics Letters 29 (1): 44–6. doi:10.1364/OL.29.000044. PMID 14719655. Bibcode: 2004OptL...29...44B. 
  27. ↑ Chremmos, I. D.; Chen, Z; Christodoulides, D. N.; Efremidis, N. K. (2012). "Bessel-like optical beams with arbitrary trajectories". Optics Letters 37 (23): 5003–5. doi:10.1364/OL.37.005003. PMID 23202118. Bibcode: 2012OptL...37.5003C. http://preprints.acmac.uoc.gr/157/1/acmac-0157.pdf. 
  28. ↑ Juanying, Z. (2013). "Observation of self-accelerating Bessel-like optical beams along arbitrary trajectories". Optics Letters 38 (4): 498–500. doi:10.1364/OL.38.000498. PMID 23455115. Bibcode: 2013OptL...38..498Z. http://preprints.acmac.uoc.gr/160/1/acmac-0160.pdf. 
  29. ↑ Jarutis, V.; Matijošius, A.; DiTrapani, P.; Piskarskas, A. (2009). "Spiraling zero-order Bessel beam". Optics Letters 34 (14): 2129–31. doi:10.1364/OL.34.002129. PMID 19823524. Bibcode: 2009OptL...34.2129J. 
  30. ↑ Morris, J. E.; Čižmár, T.; Dalgarno, H. I. C.; Marchington, R. F.; Gunn-Moore, F. J.; Dholakia, K. (2010). "Realization of curved Bessel beams: propagation around obstructions". Journal of Optics 12 (12): 124002. doi:10.1088/2040-8978/12/12/124002. Bibcode: 2010JOpt...12l4002M. 
  31. ↑ Rosen, J.; Yariv, A. (1995). "Snake beam: a paraxial arbitrary focal line". Optics Letters 20 (20): 2042–4. doi:10.1364/OL.20.002042. PMID 19862244. Bibcode: 1995OptL...20.2042R. 
  32. ↑ Zamboni-Rached, Michel (2004-08-23). "Stationary optical wave fields with arbitrary longitudinal shape by superposing equal frequency Bessel beams: Frozen Waves" (in EN). Optics Express 12 (17): 4001–4006. doi:10.1364/opex.12.004001. PMID 19483938. Bibcode: 2004OExpr..12.4001Z. 
  33. ↑ Čižmár, Tomáš; Dholakia, Kishan (2009-08-31). "Tunable Bessel light modes: engineering the axial propagation" (in EN). Optics Express 17 (18): 15558–15570. doi:10.1364/oe.17.015558. PMID 19724554. Bibcode: 2009OExpr..1715558C. 
  34. ↑ Fahrbach, Florian O.; Simon, Philipp; Rohrbach, Alexander (2010). "Microscopy with self-reconstructing beams" (in En). Nature Photonics 4 (11): 780–785. doi:10.1038/nphoton.2010.204. Bibcode: 2010NaPho...4..780F. https://www.freidok.uni-freiburg.de/dnb/download/8979. 
  35. ↑ Nylk, Jonathan; McCluskey, Kaley; Preciado, Miguel A.; Mazilu, Michael; Yang, Zhengyi; Gunn-Moore, Frank J.; Aggarwal, Sanya; Tello, Javier A. et al. (2018-04-01). "Light-sheet microscopy with attenuation-compensated propagation-invariant beams" (in en). Science Advances 4 (4): eaar4817. doi:10.1126/sciadv.aar4817. PMID 29740614. Bibcode: 2018SciA....4R4817N. 

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Bessel_beam&oldid=3282167"