Physics:Cluster-expansion approach

Short description: Quantum mechanical calculation technique

The cluster-expansion approach is a technique in quantum mechanics that systematically truncates the BBGKY hierarchy problem that arises when quantum dynamics of interacting systems is solved. This method is well suited for producing a closed set of numerically computable equations that can be applied to analyze a great variety of many-body and/or quantum-optical problems. For example, it is widely applied in semiconductor quantum optics and it can be applied to generalize the semiconductor Bloch equations and semiconductor luminescence equations.

Background

Quantum theory essentially replaces classically accurate values by a probabilistic distribution that can be formulated using, e.g., a wavefunction, a density matrix, or a phase-space distribution. Conceptually, there is always, at least formally, probability distribution behind each observable that is measured. Already in 1889, a long time before quantum physics was formulated, Thorvald N. Thiele proposed the cumulants that describe probabilistic distributions with as few quantities as possible; he called them half-invariants. The cumulants form a sequence of quantities such as mean, variance, skewness, kurtosis, and so on, that identify the distribution with increasing accuracy as more cumulants are used.

The idea of cumulants was converted into quantum physics by Fritz Coester and Hermann Kümmel with the intention of studying nuclear many-body phenomena. Later, Jiři Čížek and Josef Paldus extended the approach for quantum chemistry in order to describe many-body phenomena in complex atoms and molecules. This work introduced the basis for the coupled-cluster approach that mainly operates with many-body wavefunctions. The coupled-clusters approach is one of the most successful methods to solve quantum states of complex molecules.

In solids, the many-body wavefunction has an overwhelmingly complicated structure such that the direct wave-function-solution techniques are intractable. The cluster expansion is a variant of the coupled-clusters approach and it solves the dynamical equations of correlations instead of attempting to solve the quantum dynamics of an approximated wavefunction or density matrix. It is equally well suited to treat properties of many-body systems and quantum-optical correlations, which has made it very suitable approach for semiconductor quantum optics.

Like almost always in many-body physics or quantum optics, it is most convenient to apply the second-quantization formalism to describe the physics involved. For example, a light field is then described through Boson creation and annihilation operators [math]\displaystyle{ \hat{B}^\dagger_\mathbf{q} }[/math] and [math]\displaystyle{ \hat{B}_\mathbf{q} }[/math], respectively, where [math]\displaystyle{ \hbar\mathbf{q} }[/math] defines the momentum of a photon. The "hat" over [math]\displaystyle{ B }[/math] signifies the operator nature of the quantity. When the many-body state consists of electronic excitations of matter, it is fully defined by Fermion creation and annihilation operators [math]\displaystyle{ \hat{a}^\dagger_{\lambda,\mathbf{k}} }[/math] and [math]\displaystyle{ \hat{a}_{\lambda,\mathbf{k}} }[/math], respectively, where [math]\displaystyle{ \hbar\mathbf{k} }[/math] refers to particle's momentum while [math]\displaystyle{ \lambda }[/math] is some internal degree of freedom, such as spin or band index.

Classification of N-particle contributions

When the many-body system is studied together with its quantum-optical properties, all measurable expectation values can be expressed in the form of an N-particle expectation value

[math]\displaystyle{ \langle \hat{N} \rangle \equiv \langle \hat{B}^\dagger_1 \cdots \hat{B}^\dagger_K \ \hat{a}^\dagger_1 \cdots \hat{a}^\dagger_{N_{\hat{a}}} \hat{a}_{N_{\hat{a}}} \cdots \hat{a}_{1} \ \hat{B}_{J} \cdots \hat{B}_1 \rangle }[/math]

where [math]\displaystyle{ N=N_{\hat{B}} +N_{\hat{a}} }[/math] and [math]\displaystyle{ N_{\hat{B}}=J+K }[/math] while the explicit momentum indices are suppressed for the sake of briefness. These quantities are normally ordered, which means that all creation operators are on the left-hand side while all annihilation operators are on the right-hand side in the expectation value. It is straight forward to show that this expectation value vanishes if the amount of Fermion creation and annihilation operators are not equal.

Once the system Hamiltonian is known, one can use the Heisenberg equation of motion to generate the dynamics of a given [math]\displaystyle{ N }[/math]-particle operator. However, the many-body as well as quantum-optical interactions couple the [math]\displaystyle{ N }[/math]-particle quantities to [math]\displaystyle{ (N+1) }[/math]-particle expectation values, which is known as the Bogolyubov–Born–Green–Kirkwood–Yvon (BBGKY) hierarchy problem. More mathematically, all particles interact with each other leading to an equation structure

[math]\displaystyle{ \mathrm{i}\hbar \frac{\partial}{\partial t} \langle\hat{N}\rangle = \mathrm{T}\left[ \langle\hat{N}\rangle \right] + \mathrm{Hi}\left[ \langle\hat{N}+1\rangle \right] }[/math]

where functional [math]\displaystyle{ T }[/math] symbolizes contributions without hierarchy problem and the functional for hierarchical (Hi) coupling is symbolized by [math]\displaystyle{ \mathrm{Hi}[\langle\hat{N}+1\rangle] }[/math]. Since all levels of expectation values can be nonzero, up to the actual particle number, this equation cannot be directly truncated without further considerations.

Recursive definition of clusters

Schematic representation of the cluster-expansion-based classification. The full correlation is composed of singlets, doublets, triplets, and higher-order correlations, all uniquely defined by the cluster-expansion approach. Each blue sphere corresponds to one particle operator and yellow circles/ellipses to correlations. The number of spheres within a correlation identifies the cluster number.

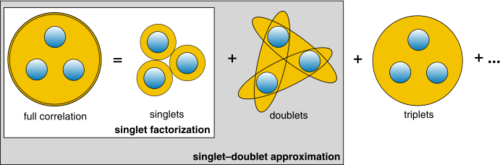
The hierarchy problem can be systematically truncated after identifying correlated clusters. The simplest definitions follow after one identifies the clusters recursively. At the lowest level, one finds the class of single-particle expectation values (singlets) that are symbolized by [math]\displaystyle{ \langle 1\rangle }[/math]. Any two-particle expectation value [math]\displaystyle{ \langle 2 \rangle }[/math] can be approximated by factorization [math]\displaystyle{ \langle 2 \rangle_\mathrm{S} = \langle 1 \rangle \langle 1 \rangle }[/math] that contains a formal sum over all possible products of single-particle expectation values. More generally, [math]\displaystyle{ \langle 1 \rangle }[/math] defines the singlets and [math]\displaystyle{ \langle N \rangle_\mathrm{S} }[/math] is the singlet factorization of an [math]\displaystyle{ N }[/math]-particle expectation value. Physically, the singlet factorization among Fermions produces the Hartree–Fock approximation while for Bosons it yields the classical approximation where Boson operators are formally replaced by a coherent amplitude, i.e., [math]\displaystyle{ \hat{B} \rightarrow \langle \hat{B} \rangle }[/math]. The singlet factorization constitutes the first level of the cluster-expansion representation.

The correlated part of [math]\displaystyle{ \langle 2 \rangle }[/math] is then the difference of the actual [math]\displaystyle{ \langle 2 \rangle }[/math] and the singlet factorization [math]\displaystyle{ \langle 2 \rangle_\mathrm{S} }[/math]. More mathematically, one finds

[math]\displaystyle{ \langle 2\rangle = \langle 2\rangle_\mathrm{S} + \Delta \langle 2\rangle }[/math]

where the [math]\displaystyle{ \Delta }[/math] contribution denotes the correlated part, i.e., [math]\displaystyle{ \Delta \langle 2\rangle = \langle 2\rangle-\langle 2\rangle_\mathrm{S} }[/math]. The next levels of identifications follow recursively by applying

[math]\displaystyle{ \begin{align} \langle 3\rangle &= \langle 3\rangle_\mathrm{S} + \langle 1\rangle\ \Delta \langle 2\rangle +\Delta \langle 3\rangle \,, \\ \langle N\rangle &= \langle N\rangle_\mathrm{S} \\ &\quad+ \langle N-2\rangle_\mathrm{S}\ \Delta \langle 2\rangle \\ &\quad+ \langle N-4\rangle_\mathrm{S}\ \Delta \langle 2\rangle\ \Delta \langle 2\rangle +\dots\\ &\quad+ \langle N-3\rangle_\mathrm{S}\ \Delta \langle 3\rangle \\ &\quad+ \langle N-5\rangle_\mathrm{S}\ \Delta \langle 3\rangle\ \Delta \langle 2\rangle +\dots\\ &\quad+ \Delta\langle N\rangle\,, \end{align} }[/math]

where each product term represents one factorization symbolically and implicitly includes a sum over all factorizations within the class of terms identified. The purely correlated part is denoted by [math]\displaystyle{ \Delta\langle N\rangle }[/math]. From these, the two-particle correlations [math]\displaystyle{ \Delta \langle 2\rangle }[/math] determine doublets while the three-particle correlations [math]\displaystyle{ \Delta \langle 3\rangle }[/math] are called triplets.

As this identification is applied recursively, one may directly identify which correlations appear in the hierarchy problem. One then determines the quantum dynamics of the correlations, yielding

[math]\displaystyle{ \mathrm{i}\hbar \frac{\partial}{\partial t} \Delta \langle\hat{N}\rangle = \mathrm{T}\left[ \Delta \langle\hat{N}\rangle \right] + \mathrm{NL} \left[\langle\hat{1}\rangle, \Delta \langle\hat{2}\rangle,\cdots, \Delta \langle\hat{N}\rangle \right] + \mathrm{Hi}\left[ \Delta \langle\hat{N}+1\rangle \right]\,, }[/math]

where the factorizations produce a nonlinear coupling [math]\displaystyle{ \mathrm{NL} \left[ \cdots \right] }[/math] among clusters. Obviously, introducing clusters cannot remove the hierarchy problem of the direct approach because the hierarchical contributions remains in the dynamics. This property and the appearance of the nonlinear terms seem to suggest complications for the applicability of the cluster-expansion approach.

However, as a major difference to a direct expectation-value approach, both many-body and quantum-optical interactions generate correlations sequentially. In several relevant problems, one indeed has a situation where only the lowest-order clusters are initially nonvanishing while the higher-order clusters build up slowly. In this situation, one can omit the hierarchical coupling, [math]\displaystyle{ \mathrm{Hi}\left[ \Delta \langle\hat{C}+1\rangle \right] }[/math], at the level exceeding [math]\displaystyle{ C }[/math]-particle clusters. As a result, the equations become closed and one only needs to compute the dynamics up to [math]\displaystyle{ C }[/math]-particle correlations in order to explain the relevant properties of the system. Since [math]\displaystyle{ C }[/math] is typically much smaller than the overall particle number, the cluster-expansion approach yields a pragmatic and systematic solution scheme for many-body and quantum-optics investigations.

Extensions

Besides describing quantum dynamics, one can naturally apply the cluster-expansion approach to represent the quantum distributions. One possibility is to represent the quantum fluctuations of a quantized light mode [math]\displaystyle{ \hat{B} }[/math] in terms of clusters, yielding the cluster-expansion representation. Alternatively, one can express them in terms of the expectation-value representation [math]\displaystyle{ \langle [\hat{B}^\dagger]^J \hat{B}^K \rangle }[/math]. In this case, the connection from [math]\displaystyle{ \langle [\hat{B}^\dagger]^J \hat{B}^K \rangle }[/math] to the density matrix is unique but can result in a numerically diverging series. This problem can be solved by introducing a cluster-expansion transformation (CET) that represents the distribution in terms of a Gaussian, defined by the singlet–doublet contributions, multiplied by a polynomial, defined by the higher-order clusters. It turns out that this formulation provides extreme convergence in representation-to-representation transformations.

This completely mathematical problem has a direct physical application. One can apply the cluster-expansion transformation to robustly project classical measurement into a quantum-optical measurement. This property is largely based on CET's ability to describe any distribution in the form where a Gaussian is multiplied by a polynomial factor. This technique is already being used to access and derive quantum-optical spectroscopy from a set of classical spectroscopy measurements, which can be performed using high-quality lasers.

See also

• BBGKY hierarchy
• Quantum-optical spectroscopy
• Semiconductor Bloch equations
• Semiconductor luminescence equations

Further reading

• Kira, M.; Koch, S. W. (2011). Semiconductor Quantum Optics. Cambridge University Press. ISBN 978-0521875097. 
• Shavitt, I.; Bartlett, R. J. (2009). Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory. Cambridge University Press. ISBN 978-0521818322.