Density matrix
| Part of a series on |
| Quantum mechanics |
|---|
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using the Born rule. It is a generalization of the more usual state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent mixed states. Mixed states arise in quantum mechanics in two different situations:
- when the preparation of the system is not fully known, and thus one must deal with a statistical ensemble of possible preparations, and
- when one wants to describe a physical system that is entangled with another, without describing their combined state; this case is typical for a system interacting with some environment.
Density matrices are thus crucial tools in areas of quantum mechanics that deal with mixed states, such as quantum statistical mechanics, open quantum systems, quantum decoherence, and quantum information.
Definition and motivation
The density matrix is a representation of a linear operator called the density operator. The density matrix is obtained from the density operator by a choice of an orthonormal basis in the underlying space. In practice, the terms density matrix and density operator are often used interchangeably.
Pick a basis with states , in a two-dimensional Hilbert space, then the density operator is represented by the matrix
where the diagonal elements are real numbers that sum to one (also called populations of the two states , ). The off-diagonal elements are complex conjugates of each other (also called coherences); they are restricted in magnitude by the requirement that be a positive semi-definite, see below.
In operator language, a density operator for a system is a positive semi-definite, Hermitian operator of trace one acting on the Hilbert space of the system.[1][2][3] This definition can be motivated by considering a situation where each pure state is prepared with probability , describing an ensemble of pure states. The probability of obtaining projective measurement result when using projectors is given by[4]:{{{1}}} which makes the density operator, defined as a convenient representation for the state of this ensemble. It is easy to check that this operator is positive semi-definite, Hermitian, and has trace one. Conversely, it follows from the spectral theorem that every operator with these properties can be written as for some states and coefficients that are non-negative and add up to one.[5][4]:{{{1}}} However, this representation will not be unique, as shown by the Schrödinger–HJW theorem.
Another motivation for the definition of density operators comes from considering local measurements on entangled states. Let be a pure entangled state in the composite Hilbert space . The probability of obtaining measurement result when measuring projectors on the Hilbert space alone is given by[4]:{{{1}}} where denotes the partial trace over the Hilbert space . This makes the operator a convenient tool to calculate the probabilities of these local measurements. It is known as the reduced density matrix of on subsystem 1. It is easy to check that this operator has all the properties of a density operator. Conversely, the Schrödinger–HJW theorem implies that all density operators can be written as for some state .
Pure and mixed states
A pure quantum state is a state that can not be written as a probabilistic mixture, or convex combination, of other quantum states.[3] There are several equivalent characterizations of pure states in the language of density operators.[6]:73 A density operator represents a pure state if and only if:
- it can be written as an outer product of a state vector with itself, that is,
- it is a projection, in particular of rank one.
- it is idempotent, that is
- it has purity one, that is,
It is important to emphasize the difference between a probabilistic mixture of quantum states and their superposition. If a physical system is prepared to be either in state or , with equal probability, it can be described by the mixed state
where and are assumed orthogonal and of dimension 2, for simplicity. On the other hand, a quantum superposition of these two states with equal probability amplitudes results in the pure state with density matrix
Unlike the probabilistic mixture, this superposition can display quantum interference.[4]:81
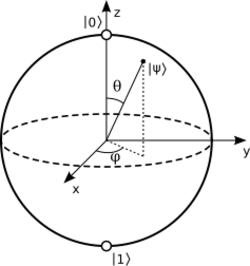
Geometrically, the set of density operators is a convex set, and the pure states are the extremal points of that set. The simplest case is that of a two-dimensional Hilbert space, known as a qubit. An arbitrary mixed state for a qubit can be written as a linear combination of the Pauli matrices, which together with the identity matrix provide a basis for
where the real numbers are the coordinates of a point within the unit ball and
Points with represent pure states, while mixed states are represented by points in the interior. This is known as the Bloch sphere picture of qubit state space.
Example: light polarization
An example of pure and mixed states is light polarization. An individual photon can be described as having right or left circular polarization, described by the orthogonal quantum states and or a superposition of the two: it can be in any state (with ), corresponding to linear, circular, or elliptical polarization. Consider now a vertically polarized photon, described by the state . If we pass it through a circular polarizer that allows either only polarized light, or only polarized light, half of the photons are absorbed in both cases. This may make it seem like half of the photons are in state and the other half in state , but this is not correct: if we pass through a linear polarizer there is no absorption whatsoever, but if we pass either state or half of the photons are absorbed.
Unpolarized light (such as the light from an incandescent light bulb) cannot be described as any state of the form (linear, circular, or elliptical polarization). Unlike polarized light, it passes through a polarizer with 50% intensity loss whatever the orientation of the polarizer; and it cannot be made polarized by passing it through any wave plate. However, unpolarized light can be described as a statistical ensemble, e. g. as each photon having either polarization or polarization with probability 1/2. The same behavior would occur if each photon had either vertical polarization or horizontal polarization with probability 1/2. These two ensembles are completely indistinguishable experimentally, and therefore they are considered the same mixed state. For this example of unpolarized light, the density operator equals[6]:75
There are also other ways to generate unpolarized light: one possibility is to introduce uncertainty in the preparation of the photon, for example, passing it through a birefringent crystal with a rough surface, so that slightly different parts of the light beam acquire different polarizations. Another possibility is using entangled states: a radioactive decay can emit two photons traveling in opposite directions, in the quantum state . The joint state of the two photons together is pure, but the density matrix for each photon individually, found by taking the partial trace of the joint density matrix, is completely mixed.[4]:106
Equivalent ensembles and purifications
A given density operator does not uniquely determine which ensemble of pure states gives rise to it; in general there are infinitely many different ensembles generating the same density matrix.[8] Those cannot be distinguished by any measurement.[9] The equivalent ensembles can be completely characterized: let be an ensemble. Then for any complex matrix such that (a partial isometry), the ensemble defined by
will give rise to the same density operator, and all equivalent ensembles are of this form.
A closely related fact is that a given density operator has infinitely many different purifications, which are pure states that generate the density operator when a partial trace is taken. Let
be the density operator generated by the ensemble , with states not necessarily orthogonal. Then for all partial isometries we have that
is a purification of , where is an orthogonal basis, and furthermore all purifications of are of this form.
Measurement
Let be an observable of the system, and suppose the ensemble is in a mixed state such that each of the pure states occurs with probability . Then the corresponding density operator equals
The expectation value of the measurement can be calculated by extending from the case of pure states:
where denotes trace. Thus, the familiar expression for pure states is replaced by
for mixed states.[6]:73
Moreover, if has spectral resolution
where is the projection operator into the eigenspace corresponding to eigenvalue , the post-measurement density operator is given by[10][11]
when outcome i is obtained. In the case where the measurement result is not known the ensemble is instead described by
If one assumes that the probabilities of measurement outcomes are linear functions of the projectors , then they must be given by the trace of the projector with a density operator. Gleason's theorem shows that in Hilbert spaces of dimension 3 or larger the assumption of linearity can be replaced with an assumption of non-contextuality.[12] This restriction on the dimension can be removed by assuming non-contextuality for POVMs as well,[13][14] but this has been criticized as physically unmotivated.[15]
Entropy
The von Neumann entropy of a mixture can be expressed in terms of the eigenvalues of or in terms of the trace and logarithm of the density operator . Since is a positive semi-definite operator, it has a spectral decomposition such that , where are orthonormal vectors, , and . Then the entropy of a quantum system with density matrix is
This definition implies that the von Neumann entropy of any pure state is zero.[16]:217 If are states that have support on orthogonal subspaces, then the von Neumann entropy of a convex combination of these states,
is given by the von Neumann entropies of the states and the Shannon entropy of the probability distribution :
When the states do not have orthogonal supports, the sum on the right-hand side is strictly greater than the von Neumann entropy of the convex combination .[4]:518
Given a density operator and a projective measurement as in the previous section, the state defined by the convex combination
which can be interpreted as the state produced by performing the measurement but not recording which outcome occurred,[7]:159 has a von Neumann entropy larger than that of , except if . It is however possible for the produced by a generalized measurement, or POVM, to have a lower von Neumann entropy than .[4]:514
The von Neumann equation for time evolution
Just as the Schrödinger equation describes how pure states evolve in time, the von Neumann equation (also known as the Liouville–von Neumann equation) describes how a density operator evolves in time. The von Neumann equation dictates that[17][18][19]
where the brackets denote a commutator.
This equation only holds when the density operator is taken to be in the Schrödinger picture, even though this equation seems at first look to emulate the Heisenberg equation of motion in the Heisenberg picture, with a crucial sign difference:
where is some Heisenberg picture operator; but in this picture the density matrix is not time-dependent, and the relative sign ensures that the time derivative of the expected value comes out the same as in the Schrödinger picture.[3]
If the Hamiltonian is time-independent, the von Neumann equation can be easily solved to yield
For a more general Hamiltonian, if is the wavefunction propagator over some interval, then the time evolution of the density matrix over that same interval is given by
Wigner functions and classical analogies
The density matrix operator may also be realized in phase space. Under the Wigner map, the density matrix transforms into the equivalent Wigner function,
The equation for the time evolution of the Wigner function, known as Moyal equation, is then the Wigner-transform of the above von Neumann equation,
where is the Hamiltonian, and is the Moyal bracket, the transform of the quantum commutator.
The evolution equation for the Wigner function is then analogous to that of its classical limit, the Liouville equation of classical physics. In the limit of vanishing Planck's constant , reduces to the classical Liouville probability density function in phase space.
Example applications
Density matrices are a basic tool of quantum mechanics, and appear at least occasionally in almost any type of quantum-mechanical calculation. Some specific examples where density matrices are especially helpful and common are as follows:
- Statistical mechanics uses density matrices, most prominently to express the idea that a system is prepared at a nonzero temperature. Constructing a density matrix using a canonical ensemble gives a result of the form , where is the inverse temperature and is the system's Hamiltonian. The normalization condition that the trace of be equal to 1 defines the partition function to be . If the number of particles involved in the system is itself not certain, then a grand canonical ensemble can be applied, where the states summed over to make the density matrix are drawn from a Fock space.[20]:174
- Quantum decoherence theory typically involves non-isolated quantum systems developing entanglement with other systems, including measurement apparatuses. Density matrices make it much easier to describe the process and calculate its consequences. Quantum decoherence explains why a system interacting with an environment transitions from being a pure state, exhibiting superpositions, to a mixed state, an incoherent combination of classical alternatives. This transition is fundamentally reversible, as the combined state of system and environment is still pure, but for all practical purposes irreversible, as the environment is a very large and complex quantum system, and it is not feasible to reverse their interaction. Decoherence is thus very important for explaining the classical limit of quantum mechanics, but cannot explain wave function collapse, as all classical alternatives are still present in the mixed state, and wave function collapse selects only one of them.[21]
- Similarly, in quantum computation, quantum information theory, open quantum systems, and other fields where state preparation is noisy and decoherence can occur, density matrices are frequently used. Noise is often modelled via a depolarizing channel or an amplitude damping channel. Quantum tomography is a process by which, given a set of data representing the results of quantum measurements, a density matrix consistent with those measurement results is computed.[22][23]
- When analyzing a system with many electrons, such as an atom or molecule, an imperfect but useful first approximation is to treat the electrons as uncorrelated or each having an independent single-particle wavefunction. This is the usual starting point when building the Slater determinant in the Hartree–Fock method. If there are electrons filling the single-particle wavefunctions , then the collection of electrons together can be characterized by a density matrix .
C*-algebraic formulation of states
It is now generally accepted that the description of quantum mechanics in which all self-adjoint operators represent observables is untenable.[24][25] For this reason, observables are identified with elements of an abstract C*-algebra A (that is one without a distinguished representation as an algebra of operators) and states are positive linear functionals on A. However, by using the GNS construction, we can recover Hilbert spaces that realize A as a subalgebra of operators.
Geometrically, a pure state on a C*-algebra A is a state that is an extreme point of the set of all states on A. By properties of the GNS construction these states correspond to irreducible representations of A.
The states of the C*-algebra of compact operators K(H) correspond exactly to the density operators, and therefore the pure states of K(H) are exactly the pure states in the sense of quantum mechanics.
The C*-algebraic formulation can be seen to include both classical and quantum systems. When the system is classical, the algebra of observables become an abelian C*-algebra. In that case the states become probability measures.
History
The formalism of density operators and matrices was introduced in 1927 by John von Neumann[26] and independently, but less systematically, by Lev Landau[27] and later in 1946 by Felix Bloch.[28] Von Neumann introduced the density matrix in order to develop both quantum statistical mechanics and a theory of quantum measurements. The name density matrix itself relates to its classical correspondence to a phase-space probability measure (probability distribution of position and momentum) in classical statistical mechanics, which was introduced by Wigner in 1932.[1]
In contrast, the motivation that inspired Landau was the impossibility of describing a subsystem of a composite quantum system by a state vector.[27]
See also
- Atomic electron transition
- Density functional theory
- Green–Kubo relations
- Green's function (many-body theory)
- Lindblad equation
- Wigner quasi-probability distribution
Notes and references
- ↑ 1.0 1.1 Fano, U. (1957). "Description of States in Quantum Mechanics by Density Matrix and Operator Techniques". Reviews of Modern Physics 29 (1): 74–93. doi:10.1103/RevModPhys.29.74. Bibcode: 1957RvMP...29...74F.
- ↑ Holevo, Alexander S. (2001). Statistical Structure of Quantum Theory. Lecture Notes in Physics. Springer. ISBN 3-540-42082-7. OCLC 318268606.
- ↑ 3.0 3.1 3.2 Hall, Brian C. (2013). "Systems and Subsystems, Multiple Particles". Quantum Theory for Mathematicians. Graduate Texts in Mathematics. 267. pp. 419–440. doi:10.1007/978-1-4614-7116-5_19. ISBN 978-1-4614-7115-8.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Nielsen, Michael; Chuang, Isaac (2000), Quantum Computation and Quantum Information, Cambridge University Press, ISBN 978-0-521-63503-5.
- ↑ Davidson, Ernest Roy (1976). Reduced Density Matrices in Quantum Chemistry. Academic Press, London.
- ↑ 6.0 6.1 6.2 Peres, Asher (1995). Concepts and Methods. Kluwer. ISBN 978-0-7923-3632-7. OCLC 901395752.
- ↑ 7.0 7.1 Wilde, Mark M. (2017). Quantum Information Theory (2nd ed.). Cambridge University Press. doi:10.1017/9781316809976.001. ISBN 978-1-107-17616-4. OCLC 973404322.
- ↑ Kirkpatrick, K. A. (February 2006). "The Schrödinger-HJW Theorem". Foundations of Physics Letters 19 (1): 95–102. doi:10.1007/s10702-006-1852-1. ISSN 0894-9875. Bibcode: 2006FoPhL..19...95K.
- ↑ Ochs, Wilhelm (1981-11-01). "Some comments on the concept of state in quantum mechanics" (in en). Erkenntnis 16 (3): 339–356. doi:10.1007/BF00211375. ISSN 1572-8420. https://doi.org/10.1007/BF00211375.
- ↑ Lüders, Gerhart (1950). "Über die Zustandsänderung durch den Messprozeß". Annalen der Physik 443 (5–8): 322. doi:10.1002/andp.19504430510. Bibcode: 1950AnP...443..322L. Translated by K. A. Kirkpatrick as Lüders, Gerhart (2006-04-03). "Concerning the state-change due to the measurement process". Annalen der Physik 15 (9): 663–670. doi:10.1002/andp.200610207. Bibcode: 2006AnP...518..663L.
- ↑ Busch, Paul; Lahti, Pekka (2009), Greenberger, Daniel; Hentschel, Klaus; Weinert, Friedel, eds., "Lüders Rule" (in en), Compendium of Quantum Physics (Springer Berlin Heidelberg): pp. 356–358, doi:10.1007/978-3-540-70626-7_110, ISBN 978-3-540-70622-9
- ↑ Gleason, Andrew M. (1957). "Measures on the closed subspaces of a Hilbert space". Indiana University Mathematics Journal 6 (4): 885–893. doi:10.1512/iumj.1957.6.56050. http://www.iumj.indiana.edu/IUMJ/FULLTEXT/1957/6/56050.
- ↑ Busch, Paul (2003). "Quantum States and Generalized Observables: A Simple Proof of Gleason's Theorem". Physical Review Letters 91 (12): 120403. doi:10.1103/PhysRevLett.91.120403. PMID 14525351. Bibcode: 2003PhRvL..91l0403B.
- ↑ Caves, Carlton M.; Fuchs, Christopher A.; Manne, Kiran K.; Renes, Joseph M. (2004). "Gleason-Type Derivations of the Quantum Probability Rule for Generalized Measurements". Foundations of Physics 34 (2): 193–209. doi:10.1023/B:FOOP.0000019581.00318.a5. Bibcode: 2004FoPh...34..193C.
- ↑ Andrzej Grudka; Paweł Kurzyński (2008). "Is There Contextuality for a Single Qubit?". Physical Review Letters 100 (16): 160401. doi:10.1103/PhysRevLett.100.160401. PMID 18518167. Bibcode: 2008PhRvL.100p0401G.
- ↑ Rieffel, Eleanor G.; Polak, Wolfgang H. (2011-03-04) (in en). Quantum Computing: A Gentle Introduction. MIT Press. ISBN 978-0-262-01506-6.
- ↑ Breuer, Heinz; Petruccione, Francesco (2002), The theory of open quantum systems, Oxford University Press, p. 110, ISBN 978-0-19-852063-4, https://books.google.com/books?id=0Yx5VzaMYm8C&pg=PA110
- ↑ Schwabl, Franz (2002), Statistical mechanics, Springer, p. 16, ISBN 978-3-540-43163-3, https://books.google.com/books?id=o-HyHvRZ4VcC&pg=PA16
- ↑ Müller-Kirsten, Harald J.W. (2008), Classical Mechanics and Relativity, World Scientific, pp. 175–179, ISBN 978-981-283-251-1
- ↑ Kardar, Mehran (2007). Statistical Physics of Particles. Cambridge University Press. ISBN 978-0-521-87342-0. OCLC 860391091.
- ↑ Schlosshauer, M. (2019). "Quantum Decoherence". Physics Reports 831: 1–57. doi:10.1016/j.physrep.2019.10.001. Bibcode: 2019PhR...831....1S.
- ↑ Granade, Christopher; Combes, Joshua; Cory, D. G. (2016-01-01). "Practical Bayesian tomography" (in en). New Journal of Physics 18 (3): 033024. doi:10.1088/1367-2630/18/3/033024. ISSN 1367-2630. Bibcode: 2016NJPh...18c3024G.
- ↑ Ardila, Luis; Heyl, Markus; Eckardt, André (28 December 2018). "Measuring the Single-Particle Density Matrix for Fermions and Hard-Core Bosons in an Optical Lattice". Physical Review Letters 121 (260401): 6. doi:10.1103/PhysRevLett.121.260401. PMID 30636128. Bibcode: 2018PhRvL.121z0401P.
- ↑ See appendix, Mackey, George Whitelaw (1963), Mathematical Foundations of Quantum Mechanics, Dover Books on Mathematics, New York: Dover Publications, ISBN 978-0-486-43517-6
- ↑ Emch, Gerard G. (1972), Algebraic methods in statistical mechanics and quantum field theory, Wiley-Interscience, ISBN 978-0-471-23900-0
- ↑ von Neumann, John (1927), "Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik", Göttinger Nachrichten 1: 245–272, https://eudml.org/doc/59230
- ↑ 27.0 27.1 "The Damping Problem in Wave Mechanics (1927)". Collected Papers of L.D. Landau. 1965. pp. 8–18. doi:10.1016/B978-0-08-010586-4.50007-9. ISBN 978-0-08-010586-4.
- ↑ Fano, Ugo (1995). "Density matrices as polarization vectors". Rendiconti Lincei 6 (2): 123–130. doi:10.1007/BF03001661.
 |
