Physics:Decay scheme

Short description: A graphical presentation of all the transitions occurring in a decay of a radioactive substance

The decay scheme of a radioactive substance is a graphical presentation of all the transitions occurring in a decay, and of their relationships. Examples are shown below.

It is useful to think of the decay scheme as placed in a coordinate system, where the vertical axis is energy, increasing from bottom to top, and the horizontal axis is the proton number, increasing from left to right. The arrows indicate the emitted particles. For the gamma rays (vertical arrows), the gamma energies are given; for the beta decay (oblique arrow), the maximum beta energy.

Examples

Decay scheme of ⁶⁰Co

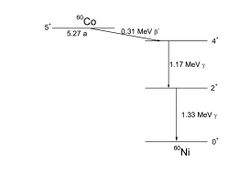
These relations can be quite complicated; a simple case is shown here: the decay scheme of the radioactive cobalt isotope cobalt-60. ⁶⁰Co decays by emitting an electron (beta decay) with a half-life of 5.272 years into an excited state of ⁶⁰Ni, which then decays very fast to the ground state of ⁶⁰Ni, via two gamma decays.

All known decay schemes can be found in the Table of Isotopes.,

Nickel is to the right of cobalt, since its proton number (28) is higher by one than that of cobalt (27). In beta decay, the proton number increases by one. For a positron decay and also for an alpha decay (see below), the oblique arrow would go from right to left since in these cases, the proton number decreases.

Since energy is conserved and since the particles emitted carry away energy, arrows can only go downward (vertically or at an angle) in a decay scheme.

Decay scheme of ¹⁹⁸Au

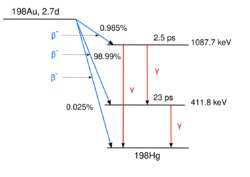
A somewhat more complicated scheme is shown here: the decay of the nuclide ¹⁹⁸Au which can be produced by irradiating natural gold in a nuclear reactor. ¹⁹⁸Au decays via beta decay to one of two excited states or to the ground state of the mercury isotope ¹⁹⁸Hg. In the figure, mercury is to the right of gold, since the atomic number of gold is 79, that of mercury is 80. The excited states decay after very short times (2.5 and 23 ps, resp.; 1 picosecond is a millionth of a millionth of a second) to the ground state.

Decay scheme of ^99mTc

While excited nuclear states are usually very short lived, decaying almost immediately after a beta decay (see above), the excited state of the technetium isotope shown here to the right is comparatively long lived. It is therefore called "metastable" (hence the "m" in ^99mTc ). It decays to the ground state via gamma decay with a half-life of 6 hours.

Decay Scheme of ²¹⁰Po

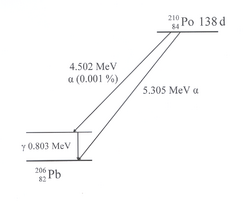
Here, to the left, we now have an alpha decay. It is the decay of the element Polonium discovered by Marie Curie, with mass number 210. The isotope ²¹⁰Po is the penultimate member of the uranium-radium-decay series; it decays into a stable lead-isotope with a half-life of 138 days. In almost all cases, the decay is via the emission of an alpha particle of 5.305 MeV. Only in one case of 100000, an alpha particle of lower energy appears; in this case, the decay leads to an excited level of ²⁰⁶Pb, which then decays to the ground state via gamma radiation.

Selection rules

⁶⁰Co Decay, with spins and parities shown

Alpha- beta- and gamma rays can only be emitted if the conservation laws (energy, angular momentum, parity) are obeyed. This leads to so-called selection rules.

Applications for gamma decay can be found in Multipolarity of gamma radiation. To discuss such a rule in a particular case, it is necessary to know angular momentum and parity for every state. The figure shows the ⁶⁰Co decay scheme again, with spins and parities given for every state.