Physics:Beta decay

In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which an atomic nucleus emits a beta particle (fast energetic electron or positron), transforming into an isobar of that nuclide. For example, beta decay of a neutron transforms it into a proton by the emission of an electron accompanied by an antineutrino; or, conversely a proton is converted into a neutron by the emission of a positron with a neutrino in so-called positron emission. Neither the beta particle nor its associated (anti-)neutrino exist within the nucleus prior to beta decay, but are created in the decay process. By this process, unstable atoms obtain a more stable ratio of protons to neutrons. The probability of a nuclide decaying due to beta and other forms of decay is determined by its nuclear binding energy. The binding energies of all existing nuclides form what is called the nuclear band or valley of stability.[1] For either electron or positron emission to be energetically possible, the energy release (see below) or Q value must be positive.
Beta decay is a consequence of the weak force, which is characterized by relatively lengthy decay times. Nucleons are composed of up quarks and down quarks,[2] and the weak force allows a quark to change its flavour by emission of a W boson leading to creation of an electron/antineutrino or positron/neutrino pair. For example, a neutron, composed of two down quarks and an up quark, decays to a proton composed of a down quark and two up quarks.
Electron capture is sometimes included as a type of beta decay,[3] because the basic nuclear process, mediated by the weak force, is the same. In electron capture, an inner atomic electron is captured by a proton in the nucleus, transforming it into a neutron, and an electron neutrino is released.
Description
The two types of beta decay are known as beta minus and beta plus. In beta minus (β−) decay, a neutron is converted to a proton, and the process creates an electron and an electron antineutrino; while in beta plus (β+) decay, a proton is converted to a neutron and the process creates a positron and an electron neutrino. β+ decay is also known as positron emission.[4]
Beta decay conserves a quantum number known as the lepton number, or the number of electrons and their associated neutrinos (other leptons are the muon and tau particles). These particles have lepton number +1, while their antiparticles have lepton number −1. Since a proton or neutron has lepton number zero, β+ decay (a positron, or antielectron) must be accompanied with an electron neutrino, while β− decay (an electron) must be accompanied by an electron antineutrino.
An example of electron emission (β− decay) is the decay of carbon-14 into nitrogen-14 with a half-life of about 5,730 years:
- 146C → 147N + e− + νe
In this form of decay, the original element becomes a new chemical element in a process known as nuclear transmutation. This new element has an unchanged mass number A, but an atomic number Z that is increased by one. As in all nuclear decays, the decaying element (in this case 146C) is known as the parent nuclide while the resulting element (in this case 147N) is known as the daughter nuclide.
Another example is the decay of hydrogen-3 (tritium) into helium-3 with a half-life of about 12.3 years:
- 31H → 32He + e− + νe
An example of positron emission (β+ decay) is the decay of magnesium-23 into sodium-23 with a half-life of about 11.3 s:
- 2312Mg → 2311Na + e+ + νe
β+ decay also results in nuclear transmutation, with the resulting element having an atomic number that is decreased by one.
The beta spectrum, or distribution of energy values for the beta particles, is continuous. The total energy of the decay process is divided between the electron, the antineutrino, and the recoiling nuclide. In the figure to the right, an example of an electron with 0.40 MeV energy from the beta decay of 210Bi is shown. In this example, the total decay energy is 1.16 MeV, so the antineutrino has the remaining energy: 1.16 MeV − 0.40 MeV = 0.76 MeV. An electron at the far right of the curve would have the maximum possible kinetic energy, leaving the energy of the neutrino to be only its small rest mass.
History
Discovery and initial characterization
Radioactivity was discovered in 1896 by Henri Becquerel in uranium, and subsequently observed by Marie and Pierre Curie in thorium and in the new elements polonium and radium. In 1899, Ernest Rutherford separated radioactive emissions into two types: alpha and beta (now beta minus), based on penetration of objects and ability to cause ionization. Alpha rays could be stopped by thin sheets of paper or aluminium, whereas beta rays could penetrate several millimetres of aluminium. In 1900, Paul Villard identified a still more penetrating type of radiation, which Rutherford identified as a fundamentally new type in 1903 and termed gamma rays. Alpha, beta, and gamma are the first three letters of the Greek alphabet.
In 1900, Becquerel measured the mass-to-charge ratio (m/e) for beta particles by the method of J.J. Thomson used to study cathode rays and identify the electron. He found that m/e for a beta particle is the same as for Thomson's electron, and therefore suggested that the beta particle is in fact an electron.[5]
In 1901, Rutherford and Frederick Soddy showed that alpha and beta radioactivity involves the transmutation of atoms into atoms of other chemical elements. In 1913, after the products of more radioactive decays were known, Soddy and Kazimierz Fajans independently proposed their radioactive displacement law, which states that beta (i.e., β−) emission from one element produces another element one place to the right in the periodic table, while alpha emission produces an element two places to the left.
Neutrinos
The study of beta decay provided the first physical evidence for the existence of the neutrino. In both alpha and gamma decay, the resulting alpha or gamma particle has a narrow energy distribution, since the particle carries the energy from the difference between the initial and final nuclear states. However, the kinetic energy distribution, or spectrum, of beta particles measured by Lise Meitner and Otto Hahn in 1911 and by Jean Danysz in 1913 showed multiple lines on a diffuse background. These measurements offered the first hint that beta particles have a continuous spectrum.[6] In 1914, James Chadwick used a magnetic spectrometer with one of Hans Geiger's new counters to make more accurate measurements which showed that the spectrum was continuous.[6][7] The distribution of beta particle energies was in apparent contradiction to the law of conservation of energy. If beta decay were simply electron emission as assumed at the time, then the energy of the emitted electron should have a particular, well-defined value.[8] For beta decay, however, the observed broad distribution of energies suggested that energy is lost in the beta decay process. This spectrum was puzzling for many years.
A second problem is related to the conservation of angular momentum. Molecular band spectra showed that the nuclear spin of nitrogen-14 is 1 (i.e., equal to the reduced Planck constant) and more generally that the spin is integral for nuclei of even mass number and half-integral for nuclei of odd mass number. This was later explained by the proton-neutron model of the nucleus.[8] Beta decay leaves the mass number unchanged, so the change of nuclear spin must be an integer. However, the electron spin is 1/2, hence angular momentum would not be conserved if beta decay were simply electron emission.
From 1920 to 1927, Charles Drummond Ellis (along with Chadwick and colleagues) further established that the beta decay spectrum is continuous. In 1933, Ellis and Nevill Mott obtained strong evidence that the beta spectrum has an effective upper bound in energy. Niels Bohr had suggested that the beta spectrum could be explained if conservation of energy was true only in a statistical sense, thus this principle might be violated in any given decay.[8]:27 However, the upper bound in beta energies determined by Ellis and Mott ruled out that notion. Now, the problem of how to account for the variability of energy in known beta decay products, as well as for conservation of momentum and angular momentum in the process, became acute.
In a famous letter written in 1930, Wolfgang Pauli attempted to resolve the beta-particle energy conundrum by suggesting that, in addition to electrons and protons, atomic nuclei also contained an extremely light neutral particle, which he called the neutron. He suggested that this "neutron" was also emitted during beta decay (thus accounting for the known missing energy, momentum, and angular momentum), but it had simply not yet been observed. In 1931, Enrico Fermi renamed Pauli's "neutron" the "neutrino" ('little neutral one' in Italian). In 1933, Fermi published his landmark theory for beta decay, where he applied the principles of quantum mechanics to matter particles, supposing that they can be created and annihilated, just as the light quanta in atomic transitions. Thus, according to Fermi, neutrinos are created in the beta-decay process, rather than contained in the nucleus; the same happens to electrons. The neutrino interaction with matter was so weak that detecting it proved a severe experimental challenge. Further indirect evidence of the existence of the neutrino was obtained by observing the recoil of nuclei that emitted such a particle after absorbing an electron. Neutrinos were finally detected directly in 1956 by the American physicists Clyde Cowan and Frederick Reines in the Cowan–Reines neutrino experiment.[9] The properties of neutrinos were (with a few minor modifications) as predicted by Pauli and Fermi.
β+ decay and electron capture
In 1934, Frédéric and Irène Joliot-Curie bombarded aluminium with alpha particles to effect the nuclear reaction 42He + 2713Al → 3015P + 10n, and observed that the product isotope 3015P emits a positron identical to those found in cosmic rays (discovered by Carl David Anderson in 1932). This was the first example of β+ decay (positron emission), which they termed artificial radioactivity since 3015P is a short-lived nuclide which does not exist in nature. In recognition of their discovery, the couple were awarded the Nobel Prize in Chemistry in 1935.[10]
The theory of electron capture was first discussed by Gian-Carlo Wick in a 1934 paper, and then developed by Hideki Yukawa and others. K-electron capture was first observed in 1937 by Luis Alvarez, in the nuclide 48V.[11][12][13] Alvarez went on to study electron capture in 67Ga and other nuclides.[11][14][15]
Non-conservation of parity
In 1956, Tsung-Dao Lee and Chen Ning Yang noticed that there was no evidence that parity was conserved in weak interactions, and so they postulated that this symmetry may not be preserved by the weak force. They sketched the design for an experiment for testing conservation of parity in the laboratory.[16] Later that year, Chien-Shiung Wu and coworkers conducted the Wu experiment showing an asymmetrical beta decay of 60Co at cold temperatures that proved that parity is not conserved in beta decay.[17][18] This surprising result overturned long-held assumptions about parity and the weak force. In recognition of their theoretical work, Lee and Yang were awarded the Nobel Prize for Physics in 1957. However Wu, who was female, was not awarded the Nobel prize.[19]
β− decay
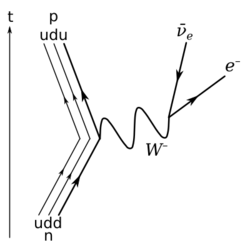
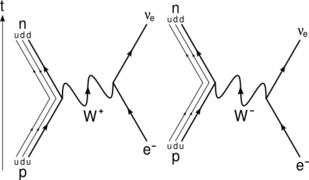
In β− decay, the weak interaction converts an atomic nucleus into a nucleus with atomic number increased by one, while emitting an electron (e−) and an electron antineutrino (νe). β− decay generally occurs in neutron-rich nuclei.[22] The generic equation is:
- AZX → AZ+1X′ + e− + νe[1]
where A and Z are the mass number and atomic number of the decaying nucleus, and X and X′ are the initial and final elements, respectively.
Another example is when the free neutron (10n) decays by β− decay into a proton (p):
- n → p + e− + νe.
At the fundamental level (as depicted in the Feynman diagram on the right), this is caused by the conversion of the negatively charged (−1/3 e) down quark to the positively charged (+2/3 e) up quark by emission of a W− boson; the W− boson subsequently decays into an electron and an electron antineutrino:
- d → u + e− + νe.
β+ decay
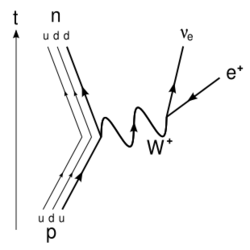
In β+ decay, or positron emission, the weak interaction converts an atomic nucleus into a nucleus with atomic number decreased by one, while emitting a positron (e+) and an electron neutrino (νe). β+ decay generally occurs in proton-rich nuclei. The generic equation is:
- AZX → AZ−1X′ + e+ + νe[1]
This may be considered as the decay of a proton inside the nucleus to a neutron:
- p → n + e+ + νe[1]
However, β+ decay cannot occur in an isolated proton because it requires energy, due to the mass of the neutron being greater than the mass of the proton. β+ decay can only happen inside nuclei when the daughter nucleus has a greater binding energy (and therefore a lower total energy) than the mother nucleus. The difference between these energies goes into the reaction of converting a proton into a neutron, a positron, and a neutrino and into the kinetic energy of these particles. This process is opposite to negative beta decay, in that the weak interaction converts a proton into a neutron by converting an up quark into a down quark resulting in the emission of a W+ or the absorption of a W−. When a W+ boson is emitted, it decays into a positron and an electron neutrino:
- u → d + e+ + νe.
Electron capture (K-capture/L-capture)
In all cases where β+ decay (positron emission) of a nucleus is allowed energetically, so too is electron capture allowed. This is a process during which a nucleus captures one of its atomic electrons, resulting in the emission of a neutrino:
- AZX + e− → AZ−1X′ + νe
An example of electron capture is one of the decay modes of krypton-81 into bromine-81:
- 8136Kr + e− → 8135Br + νe
All emitted neutrinos are of the same energy. In proton-rich nuclei where the energy difference between the initial and final states is less than mec2, β+ decay is not energetically possible, and electron capture is the sole decay mode.[23]
If the captured electron comes from the innermost shell of the atom, the K-shell, which has the highest probability to interact with the nucleus, the process is called K-capture.[24] If it comes from the L-shell, the process is called L-capture, etc.
Electron capture is a competing (simultaneous) decay process for all nuclei that can undergo β+ decay. The converse, however, is not true: electron capture is the only type of decay that is allowed in proton-rich nuclides that do not have sufficient energy to emit a positron and neutrino.[23]
Nuclear transmutation
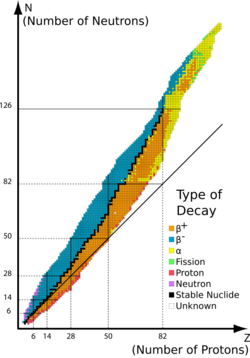
If the proton and neutron are part of an atomic nucleus, the above described decay processes transmute one chemical element into another. For example:
13755Cs → 13756Ba + e− + Electron Antineutrino (beta minus decay) 2211Na → 2210Ne + Positron + Electron Neutrino (beta plus decay) 2211Na + e− → 2210Ne + Electron Neutrino (electron capture)
Beta decay does not change the number (A) of nucleons in the nucleus, but changes only its charge Z. Thus the set of all nuclides with the same A can be introduced; these isobaric nuclides may turn into each other via beta decay. For a given A there is one that is most stable. It is said to be beta stable, because it presents a local minimum of the mass excess: if such a nucleus has (A, Z) numbers, the neighbour nuclei (A, Z−1) and (A, Z+1) have higher mass excess and can beta decay into (A, Z), but not vice versa. For all odd mass numbers A, there is only one known beta-stable isobar. For even A, there are up to three different beta-stable isobars experimentally known; for example, 12450Sn, 12452Te, and 12454Xe are all beta-stable. There are about 350 known beta-decay stable nuclides.[25]
Competition of beta decay types
Usually unstable nuclides are clearly either "neutron rich" or "proton rich", with the former undergoing beta decay and the latter undergoing electron capture (or more rarely, due to the higher energy requirements, positron decay). However, in a few cases of odd-proton, odd-neutron radionuclides, it may be energetically favorable for the radionuclide to decay to an even-proton, even-neutron isobar either by undergoing beta-positive or beta-negative decay. An often-cited example is the single isotope 6429Cu (29 protons, 35 neutrons), which illustrates three types of beta decay in competition. Copper-64 has a half-life of about 12.7 hours. This isotope has one unpaired proton and one unpaired neutron, so either the proton or the neutron can decay. This particular nuclide (though not all nuclides in this situation) is almost equally likely to decay through proton decay by positron emission (18%) or electron capture (43%) to 6428Ni, as it is through neutron decay by electron emission (39%) to 6430Zn.[26]
Stability of naturally occurring nuclides
Most naturally occurring nuclides on earth are beta stable. Nuclides that are not beta stable have half-lives ranging from under a second to periods of time significantly greater than the age of the universe. One common example of a long-lived isotope is the odd-proton odd-neutron nuclide 4019K, which undergoes all three types of beta decay (β−, β+ and electron capture) with a half-life of 1.277×109 years.[27]
Conservation rules for beta decay
Baryon number is conserved
[math]\displaystyle{ B=\frac{n_q - n_{\bar{q}}}{3} }[/math] where
- [math]\displaystyle{ n_q }[/math] is the number of constituent quarks, and
- [math]\displaystyle{ n_{\overline{q}} }[/math] is the number of constituent antiquarks.
Beta decay just changes neutron to proton or, in the case of positive beta decay (electron capture) proton to neutron so the number of individual quarks doesn't change. It is only the baryon flavor that changes, here labelled as the isospin.
Up and down quarks have total isospin [math]\displaystyle{ I=\frac{1}{2} }[/math] and isospin projections [math]\displaystyle{ I_\text{z}=\begin{cases} \frac{1}{2} & \text{up quark} \\ -\frac{1}{2} & \text{down quark} \end{cases} }[/math]
All other quarks have I = 0.
In general [math]\displaystyle{ I_\text{z}=\frac{1}{2} (n_\text{u} - n_\text{d}) }[/math]
Lepton number is conserved
[math]\displaystyle{ L \equiv n_{\ell} - n_{\bar{\ell}} }[/math]
so all leptons have assigned a value of +1, antileptons −1, and non-leptonic particles 0. [math]\displaystyle{ \begin{matrix} & \text{n} & \rightarrow & \text{p} & + & \text{e}^- & + & \bar{\nu}_\text{e} \\ L: & 0 &=& 0 & + & 1 & - & 1 \end{matrix} }[/math]
Angular momentum
For allowed decays, the net orbital angular momentum is zero, hence only spin quantum numbers are considered.
The electron and antineutrino are fermions, spin-1/2 objects, therefore they may couple to total [math]\displaystyle{ S=1 }[/math] (parallel) or [math]\displaystyle{ S=0 }[/math] (anti-parallel).
For forbidden decays, orbital angular momentum must also be taken into consideration.
Energy release
The Q value is defined as the total energy released in a given nuclear decay. In beta decay, Q is therefore also the sum of the kinetic energies of the emitted beta particle, neutrino, and recoiling nucleus. (Because of the large mass of the nucleus compared to that of the beta particle and neutrino, the kinetic energy of the recoiling nucleus can generally be neglected.) Beta particles can therefore be emitted with any kinetic energy ranging from 0 to Q.[1] A typical Q is around 1 MeV, but can range from a few keV to a few tens of MeV.
Since the rest mass of the electron is 511 keV, the most energetic beta particles are ultrarelativistic, with speeds very close to the speed of light. In the case of 187Re, the maximum speed of the beta particle is only 9.8% of the speed of light.
The following table gives some examples:
| Isotope | Energy (keV) |
Decay mode | Comments |
|---|---|---|---|
| free Neutron |
782.33 | β− | |
| 3H (Tritium) |
18.59 | β− | Second lowest known β− energy, being used in the KATRIN experiment. |
| 11C | 960.4 1982.4 |
β+ ε |
|
| 14C | 156.475 | β− | |
| 20F | 5390.86 | β− | |
| 37K | 5125.48 6147.48 |
β+ ε |
|
| 163Ho | 2.555 | ε | |
| 187Re | 2.467 | β− | Lowest known β− energy, being used in the Microcalorimeter Arrays for a Rhenium Experiment experiment |
| 210Bi | 1162.2 | β− |
β− decay
Consider the generic equation for beta decay
- AZX → AZ+1X′ + e− + νe.
The Q value for this decay is
- [math]\displaystyle{ Q=\left[m_N\left(\ce{^\mathit{A}_\mathit{Z}X}\right) - m_N\left(\ce{^\mathit{A}_{\mathit{Z}+1}X'}\right)-m_e-m_{\overline\nu_e}\right]c^2 }[/math],
where [math]\displaystyle{ m_N\left(\ce{^\mathit{A}_\mathit{Z}X}\right) }[/math] is the mass of the nucleus of the AZX atom, [math]\displaystyle{ m_e }[/math] is the mass of the electron, and [math]\displaystyle{ m_{\overline\nu_e} }[/math] is the mass of the electron antineutrino. In other words, the total energy released is the mass energy of the initial nucleus, minus the mass energy of the final nucleus, electron, and antineutrino. The mass of the nucleus mN is related to the standard atomic mass m by [math]\displaystyle{ m\left(\ce{^\mathit{A}_\mathit{Z}X}\right)c^2=m_N\left(\ce{^\mathit{A}_\mathit{Z}X}\right)c^2 + Z m_e c^2-\sum_{i=1}^Z B_i. }[/math] That is, the total atomic mass is the mass of the nucleus, plus the mass of the electrons, minus the sum of all electron binding energies Bi for the atom. This equation is rearranged to find [math]\displaystyle{ m_N\left(\ce{^\mathit{A}_\mathit{Z}X}\right) }[/math], and [math]\displaystyle{ m_N\left(\ce{^\mathit{A}_{\mathit{Z}+1}X'}\right) }[/math] is found similarly. Substituting these nuclear masses into the Q-value equation, while neglecting the nearly-zero antineutrino mass and the difference in electron binding energies, which is very small for high-Z atoms, we have [math]\displaystyle{ Q=\left[m\left(\ce{^\mathit{A}_\mathit{Z}X}\right)-m\left(\ce{^\mathit{A}_{\mathit{Z}+1}X'}\right)\right]c^2 }[/math] This energy is carried away as kinetic energy by the electron and antineutrino.
Because the reaction will proceed only when the Q value is positive, β− decay can occur when the mass of atom AZX is greater than the mass of atom AZ+1X′.[28]
β+ decay
The equations for β+ decay are similar, with the generic equation
- AZX → AZ−1X′ + e+ + νe
giving [math]\displaystyle{ Q=\left[m_N\left(\ce{^\mathit{A}_\mathit{Z}X}\right) - m_N\left(\ce{^\mathit{A}_{\mathit{Z}-1}X'}\right)-m_e-m_{\nu_e}\right]c^2. }[/math] However, in this equation, the electron masses do not cancel, and we are left with [math]\displaystyle{ Q=\left[m\left(\ce{^\mathit{A}_\mathit{Z}X}\right)-m\left(\ce{^\mathit{A}_{\mathit{Z}-1}X'}\right)-2m_e\right]c^2. }[/math]
Because the reaction will proceed only when the Q value is positive, β+ decay can occur when the mass of atom AZX exceeds that of AZ-1X′ by at least twice the mass of the electron.[28]
Electron capture
The analogous calculation for electron capture must take into account the binding energy of the electrons. This is because the atom will be left in an excited state after capturing the electron, and the binding energy of the captured innermost electron is significant. Using the generic equation for electron capture
- AZX + e− → AZ−1X′ + νe
we have [math]\displaystyle{ Q=\left[m_N\left(\ce{^\mathit{A}_\mathit{Z}X}\right) + m_e - m_N\left(\ce{^\mathit{A}_{\mathit{Z}-1}X'}\right)-m_{\nu_e}\right]c^2, }[/math] which simplifies to [math]\displaystyle{ Q=\left[m\left(\ce{^\mathit{A}_\mathit{Z}X}\right) - m\left(\ce{^\mathit{A}_{\mathit{Z}-1}X'}\right)\right]c^2-B_n, }[/math] where Bn is the binding energy of the captured electron.
Because the binding energy of the electron is much less than the mass of the electron, nuclei that can undergo β+ decay can always also undergo electron capture, but the reverse is not true.[28]
Beta emission spectrum
Beta decay can be considered as a perturbation as described in quantum mechanics, and thus Fermi's Golden Rule can be applied. This leads to an expression for the kinetic energy spectrum N(T) of emitted betas as follows:[29]
[math]\displaystyle{ N(T) = C_L(T) F(Z,T) p E (Q-T)^2 }[/math]
where T is the kinetic energy, CL is a shape function that depends on the forbiddenness of the decay (it is constant for allowed decays), F(Z, T) is the Fermi Function (see below) with Z the charge of the final-state nucleus, E = T + mc2 is the total energy, [math]\displaystyle{ p = \sqrt{(E/c)^2 - (mc)^2} }[/math] is the momentum, and Q is the Q value of the decay. The kinetic energy of the emitted neutrino is given approximately by Q minus the kinetic energy of the beta.
As an example, the beta decay spectrum of 210Bi (originally called RaE) is shown to the right.
Fermi function
The Fermi function that appears in the beta spectrum formula accounts for the Coulomb attraction / repulsion between the emitted beta and the final state nucleus. Approximating the associated wavefunctions to be spherically symmetric, the Fermi function can be analytically calculated to be:[30]
[math]\displaystyle{ F(Z,T)=\frac{2 (1+S)}{\Gamma(1+2S)^2} (2 p \rho)^{2S-2} e^{\pi \eta} |\Gamma(S+i \eta)|^2, }[/math]
where p is the final momentum, Γ the Gamma function, and (if α is the fine-structure constant and rN the radius of the final state nucleus) [math]\displaystyle{ S = \sqrt{1 - \alpha^2 Z^2} }[/math], [math]\displaystyle{ \eta = \pm Ze^2E/(\hbar cp) }[/math] (+ for electrons, − for positrons), and [math]\displaystyle{ \rho = r_N/\hbar }[/math].
For non-relativistic betas (Q ≪ mec2), this expression can be approximated by:[31]
[math]\displaystyle{ F(Z,T) \approx \frac{2 \pi \eta}{1 - e^{- 2 \pi \eta}}. }[/math]
Other approximations can be found in the literature.[32][33]
Kurie plot
A Kurie plot (also known as a Fermi–Kurie plot) is a graph used in studying beta decay developed by Franz N. D. Kurie, in which the square root of the number of beta particles whose momenta (or energy) lie within a certain narrow range, divided by the Fermi function, is plotted against beta-particle energy.[34][35] It is a straight line for allowed transitions and some forbidden transitions, in accord with the Fermi beta-decay theory. The energy-axis (x-axis) intercept of a Kurie plot corresponds to the maximum energy imparted to the electron/positron (the decay's Q value). With a Kurie plot one can find the limit on the effective mass of a neutrino.[36]
Helicity (polarization) of neutrinos, electrons and positrons emitted in beta decay
After the discovery of parity non-conservation (see History), it was found that, in beta decay, electrons are emitted mostly with negative helicity, i.e., they move, naively speaking, like left-handed screws driven into a material (they have negative longitudinal polarization).[37] Conversely, positrons have mostly positive helicity, i.e., they move like right-handed screws. Neutrinos (emitted in positron decay) have negative helicity, while antineutrinos (emitted in electron decay) have positive helicity.[38]
The higher the energy of the particles, the higher their polarization.
Types of beta decay transitions
Beta decays can be classified according to the angular momentum (L value) and total spin (S value) of the emitted radiation. Since total angular momentum must be conserved, including orbital and spin angular momentum, beta decay occurs by a variety of quantum state transitions to various nuclear angular momentum or spin states, known as "Fermi" or "Gamow–Teller" transitions. When beta decay particles carry no angular momentum (L = 0), the decay is referred to as "allowed", otherwise it is "forbidden".
Other decay modes, which are rare, are known as bound state decay and double beta decay.
Fermi transitions
A Fermi transition is a beta decay in which the spins of the emitted electron (positron) and anti-neutrino (neutrino) couple to total spin [math]\displaystyle{ S=0 }[/math], leading to an angular momentum change [math]\displaystyle{ \Delta J=0 }[/math] between the initial and final states of the nucleus (assuming an allowed transition). In the non-relativistic limit, the nuclear part of the operator for a Fermi transition is given by [math]\displaystyle{ \mathcal{O}_{F}=G_{V}\sum_{a} \hat{\tau}_{a\pm} }[/math] with [math]\displaystyle{ G_V }[/math] the weak vector coupling constant, [math]\displaystyle{ \tau_{\pm} }[/math] the isospin raising and lowering operators, and [math]\displaystyle{ a }[/math] running over all protons and neutrons in the nucleus.
Gamow–Teller transitions
A Gamow–Teller transition is a beta decay in which the spins of the emitted electron (positron) and anti-neutrino (neutrino) couple to total spin [math]\displaystyle{ S=1 }[/math], leading to an angular momentum change [math]\displaystyle{ \Delta J=0,\pm 1 }[/math] between the initial and final states of the nucleus (assuming an allowed transition). In this case, the nuclear part of the operator is given by [math]\displaystyle{ \mathcal{O}_{GT}=G_{A}\sum_{a} \hat{\sigma}_{a}\hat{\tau}_{a\pm} }[/math] with [math]\displaystyle{ G_{A} }[/math] the weak axial-vector coupling constant, and [math]\displaystyle{ \sigma }[/math] the spin Pauli matrices, which can produce a spin-flip in the decaying nucleon.
Forbidden transitions
When L > 0, the decay is referred to as "forbidden". Nuclear selection rules require high L values to be accompanied by changes in nuclear spin (J) and parity (π). The selection rules for the Lth forbidden transitions are: [math]\displaystyle{ \Delta J=L-1, L, L+1; \Delta \pi=(-1)^L, }[/math] where Δπ = 1 or −1 corresponds to no parity change or parity change, respectively. The special case of a transition between isobaric analogue states, where the structure of the final state is very similar to the structure of the initial state, is referred to as "superallowed" for beta decay, and proceeds very quickly. The following table lists the ΔJ and Δπ values for the first few values of L:
| Forbiddenness | ΔJ | Δπ |
|---|---|---|
| Superallowed | 0 | No |
| Allowed | 0, 1 | No |
| First forbidden | 0, 1, 2 | Yes |
| Second forbidden | 1, 2, 3 | No |
| Third forbidden | 2, 3, 4 | Yes |
Rare decay modes
Bound-state β− decay
A very small minority of free neutron decays (about four per million) are so-called "two-body decays", in which the proton, electron and antineutrino are produced, but the electron fails to gain the 13.6 eV energy necessary to escape the proton, and therefore simply remains bound to it, as a neutral hydrogen atom.[39] In this type of beta decay, in essence all of the neutron decay energy is carried off by the antineutrino.
For fully ionized atoms (bare nuclei), it is possible in likewise manner for electrons to fail to escape the atom, and to be emitted from the nucleus into low-lying atomic bound states (orbitals). This cannot occur for neutral atoms with low-lying bound states which are already filled by electrons.
Bound-state β decays were predicted by Daudel, Jean, and Lecoin in 1947,[40] and the phenomenon in fully ionized atoms was first observed for 163Dy66+ in 1992 by Jung et al. of the Darmstadt Heavy-Ion Research Center. Although neutral 163Dy is a stable isotope, the fully ionized 163Dy66+ undergoes β decay into the K and L shells with a half-life of 47 days.[41] The resulting nucleus - 163Ho - is stable only in the fully ionized state and will decay via electron capture into 163Dy in the neutral state. The half life for neutral 163Ho is 4750 years.
Another possibility is that a fully ionized atom undergoes greatly accelerated β decay, as observed for 187Re by Bosch et al., also at Darmstadt. Neutral 187Re does undergo β decay with a half-life of 41.6×109 years,[42] but for fully ionized 187Re75+ this is shortened to only 32.9 years.[43] For comparison the variation of decay rates of other nuclear processes due to chemical environment is less than 1%. Due to the difference in the price of rhenium and osmium and the high share of 187Re in rhenium samples found on earth, this could some day be of commercial interest in the synthesis of precious metals.[citation needed]
Double beta decay
Some nuclei can undergo double beta decay (ββ decay) where the charge of the nucleus changes by two units. Double beta decay is difficult to study, as the process has an extremely long half-life. In nuclei for which both β decay and ββ decay are possible, the rarer ββ decay process is effectively impossible to observe. However, in nuclei where β decay is forbidden but ββ decay is allowed, the process can be seen and a half-life measured.[44] Thus, ββ decay is usually studied only for beta stable nuclei. Like single beta decay, double beta decay does not change A; thus, at least one of the nuclides with some given A has to be stable with regard to both single and double beta decay.
"Ordinary" double beta decay results in the emission of two electrons and two antineutrinos. If neutrinos are Majorana particles (i.e., they are their own antiparticles), then a decay known as neutrinoless double beta decay will occur. Most neutrino physicists believe that neutrinoless double beta decay has never been observed.[44]
See also
- Common beta emitters
- Neutrino
- Betavoltaics
- Particle radiation
- Radionuclide
- Tritium illumination, a form of fluorescent lighting powered by beta decay
- Pandemonium effect
- Total absorption spectroscopy
References
- ↑ Jump up to: 1.0 1.1 1.2 1.3 1.4 Konya, J.; Nagy, N. M. (2012). Nuclear and Radio-chemistry. Elsevier. pp. 74–75. ISBN 978-0-12-391487-3.
- ↑ Bijker, R.; Santopinto, E. (2015). "Valence and sea quarks in the nucleon". Journal of Physics 578 (1): 012015. doi:10.1088/1742-6596/578/1/012015. Bibcode: 2015JPhCS.578a2015B.
- ↑ Cottingham, W. N.; Greenwood, D. A. (1986). An introduction to nuclear physics. Cambridge University Press. p. 40. ISBN 978-0-521-31960-7. https://archive.org/details/introductiontonu0000cott/page/40.
- ↑ Basdevant, J.-L.; Rich, J.; Spiro, M. (2005). Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology. Springer. ISBN 978-0-387-01672-6.
- ↑ L'Annunziata, Michael (2012). Handbook of Radioactivity Analysis (Third ed.). Elsevier Inc.. p. 3. ISBN 978-0-12-384874-1. https://books.google.com/books?id=S4FrejzJy0cC&pg=PA3. Retrieved 4 October 2017.
- ↑ Jump up to: 6.0 6.1 Jensen, C. (2000). Controversy and Consensus: Nuclear Beta Decay 1911-1934. Birkhäuser Verlag. ISBN 978-3-7643-5313-1. https://www.springer.com/birkhauser/physics/book/978-3-7643-5313-1.
- ↑ Chadwick, J. (1914). "Intensitätsverteilung im magnetischen Spektren der β-Strahlen von Radium B + C" (in de). Verhandlungen der Deutschen Physikalischen Gesellschaft 16: 383–391.
- ↑ Jump up to: 8.0 8.1 8.2 Brown, L. M. (1978). "The idea of the neutrino". Physics Today 31 (9): 23–8. doi:10.1063/1.2995181. Bibcode: 1978PhT....31i..23B.
- ↑ Cowan, C. L. Jr.; Reines, F.; Harrison, F. B.; Kruse, H. W.; McGuire, A. D. (1956). "Detection of the Free Neutrino: a Confirmation". Science 124 (3212): 103–104. doi:10.1126/science.124.3212.103. PMID 17796274. Bibcode: 1956Sci...124..103C.
- ↑ "The Nobel Prize in Chemistry 1935". https://www.nobelprize.org/nobel_prizes/chemistry/laureates/1935/.
- ↑ Jump up to: 11.0 11.1 Segré, E. (1987). "K-Electron Capture by Nuclei". in Trower, P. W.. Discovering Alvarez: Selected Works of Luis W. Alvarez. University of Chicago Press. pp. 11–12. ISBN 978-0-226-81304-2. https://archive.org/details/discoveringalvar0000alva/page/11.
- ↑ "The Nobel Prize in Physics 1968: Luis Alvarez". The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1968/alvarez-bio.html.
- ↑ Alvarez, L. W. (1937). "Nuclear K Electron Capture". Physical Review 52 (2): 134–135. doi:10.1103/PhysRev.52.134. Bibcode: 1937PhRv...52..134A.
- ↑ Alvarez, L. W. (1938). "Electron Capture and Internal Conversion in Gallium 67". Physical Review 53 (7): 606. doi:10.1103/PhysRev.53.606. Bibcode: 1938PhRv...53..606A.
- ↑ Alvarez, L. W. (1938). "The Capture of Orbital Electrons by Nuclei". Physical Review 54 (7): 486–497. doi:10.1103/PhysRev.54.486. Bibcode: 1938PhRv...54..486A.
- ↑ Lee, T. D.; Yang, C. N. (1956). "Question of Parity Conservation in Weak Interactions". Physical Review 104 (1): 254–258. doi:10.1103/PhysRev.104.254. Bibcode: 1956PhRv..104..254L.
- ↑ Wu, C.-S.; Ambler, E.; Hayward, R. W.; Hoppes, D. D.; Hudson, R. P. (1957). "Experimental Test of Parity Conservation in Beta Decay". Physical Review 105 (4): 1413–1415. doi:10.1103/PhysRev.105.1413. Bibcode: 1957PhRv..105.1413W.
- ↑ Weinstock, Maia. "Channeling Ada Lovelace: Chien-Shiung Wu, Courageous Hero of Physics". http://blogs.scientificamerican.com/guest-blog/2013/10/15/channeling-ada-lovelace-chien-shiung-wu-courageous-hero-of-physics/.
- ↑ "The Nobel Prize in Physics 1957". The Nobel Foundation. https://www.nobelprize.org/nobel_prizes/physics/laureates/1957/.
- ↑ Ivanov, A. N.; Höllwieser, R.; Troitskaya, N. I.; Wellenzohn, M.; Berdnikov, Ya. A. (2017-06-26). "Precision theoretical analysis of neutron radiative beta decay to order O ( α 2 / π 2 )" (in en). Physical Review D 95 (11): 113006. doi:10.1103/PhysRevD.95.113006. ISSN 2470-0010. Bibcode: 2017PhRvD..95k3006I.
- ↑ Ivanov, A. N.; Höllwieser, R.; Troitskaya, N. I.; Wellenzohn, M.; Berdnikov, Ya. A. (2018-11-30). "Gauge properties of hadronic structure of nucleon in neutron radiative beta decay to order O(α/π) in standard V − A effective theory with QED and linear sigma model of strong low-energy interactions" (in en). International Journal of Modern Physics A 33 (33): 1850199. doi:10.1142/S0217751X18501993. ISSN 0217-751X.
- ↑ Loveland, W. D. (2005). Modern Nuclear Chemistry. John Wiley & Sons. p. 232. ISBN 978-0-471-11532-8. https://books.google.com/books?id=ZAHJkrJlwbYC&pg=PA233.
- ↑ Jump up to: 23.0 23.1 Zuber, K. (2011). Neutrino Physics (2nd ed.). CRC Press. p. 466. ISBN 978-1-4200-6471-1.
- ↑ Jevremovic, T. (2009). Nuclear Principles in Engineering. Springer Science + Business Media. p. 201. ISBN 978-0-387-85608-7. https://books.google.com/books?id=tEM9TCfAe7EC&pg=PA201.
- ↑ "Interactive Chart of Nuclides". National Nuclear Data Center, Brookhaven National Laboratory. http://www.nndc.bnl.gov/chart/.
- ↑ "WWW Table of Radioactive Isotopes, Copper 64". LBNL Isotopes Project. Lawrence Berkeley National Laboratory. http://ie.lbl.gov/toi/nuclide.asp?iZA=290064.
- ↑ "WWW Table of Radioactive Isotopes, Potassium 40". LBNL Isotopes Project. Lawrence Berkeley National Laboratory. http://ie.lbl.gov/toi/nuclide.asp?iZA=190040.
- ↑ Jump up to: 28.0 28.1 28.2 Kenneth S. Krane (5 November 1987). Introductory Nuclear Physics. Wiley. ISBN 978-0-471-80553-3. https://books.google.com/books?id=ConwAAAAMAAJ.
- ↑ Nave, C. R.. "Energy and Momentum Spectra for Beta Decay". HyperPhysics. http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/beta2.html.
- ↑ Fermi, E. (1934). "Versuch einer Theorie der β-Strahlen. I". Zeitschrift für Physik 88 (3–4): 161–177. doi:10.1007/BF01351864. Bibcode: 1934ZPhy...88..161F.
- ↑ Mott, N. F.; Massey, H. S. W. (1933). The Theory of Atomic Collisions. Clarendon Press.
- ↑ Venkataramaiah, P.; Gopala, K.; Basavaraju, A.; Suryanarayana, S. S.; Sanjeeviah, H. (1985). "A simple relation for the Fermi function". Journal of Physics G 11 (3): 359–364. doi:10.1088/0305-4616/11/3/014. Bibcode: 1985JPhG...11..359V.
- ↑ Schenter, G. K.; Vogel, P. (1983). "A simple approximation of the fermi function in nuclear beta decay". Nuclear Science and Engineering 83 (3): 393–396. doi:10.13182/NSE83-A17574.
- ↑ "The Radiations Emitted from Artificially Produced Radioactive Substances. I. The Upper Limits and Shapes of the β-Ray Spectra from Several Elements". Physical Review 49 (5): 368–381. 1936. doi:10.1103/PhysRev.49.368. Bibcode: 1936PhRv...49..368K.
- ↑ "On the Use of the Kurie Plot". Physical Review 73 (10): 1207. 1948. doi:10.1103/PhysRev.73.1207. Bibcode: 1948PhRv...73.1207K.
- ↑ Rodejohann, W. (2012). "Neutrinoless double beta decay and neutrino physics". Journal of Physics G: Nuclear and Particle Physics 39 (12): 124008. doi:10.1088/0954-3899/39/12/124008. Bibcode: 2012JPhG...39l4008R.
- ↑ Frauenfelder, H. (1957). "Parity and the Polarization of Electrons fromCo60". Physical Review 106 (2): 386–387. doi:10.1103/physrev.106.386. Bibcode: 1957PhRv..106..386F.
- ↑ Konopinski, E. J.; Rose, M. E. (1966). "The Theory of nuclear Beta Decay". in Siegbhan, K.. Alpha-, Beta- and Gamma-Ray Spectroscopy. 2. North-Holland Publishing Company.
- ↑ An Overview Of Neutron Decay J. Byrne in Quark-Mixing, CKM Unitarity (H. Abele and D. Mund, 2002), see p.XV
- ↑ Daudel, Raymond; Jean, Maurice; Lecoin, Marcel (1947). "Sur la possibilité d'existence d'un type particulier de radioactivité phénomène de création e". J. Phys. Radium 8 (8): 238–243. doi:10.1051/jphysrad:0194700808023800. https://hal.archives-ouvertes.fr/jpa-00234057/document.
- ↑ Jung, M. (1992). "First observation of bound-state β− decay". Physical Review Letters 69 (15): 2164–2167. doi:10.1103/PhysRevLett.69.2164. PMID 10046415. Bibcode: 1992PhRvL..69.2164J.
- ↑ Smoliar, M.I.; Walker, R.J.; Morgan, J.W. (1996). "Re-Os ages of group IIA, IIIA, IVA, and IVB iron meteorites". Science 271 (5252): 1099–1102. doi:10.1126/science.271.5252.1099. Bibcode: 1996Sci...271.1099S.
- ↑ Bosch, F. (1996). "Observation of bound-state beta minus decay of fully ionized 187Re: 187Re–187Os Cosmochronometry". Physical Review Letters 77 (26): 5190–5193. doi:10.1103/PhysRevLett.77.5190. PMID 10062738. Bibcode: 1996PhRvL..77.5190B.
- ↑ Jump up to: 44.0 44.1 Bilenky, S. M. (2010). "Neutrinoless double beta-decay". Physics of Particles and Nuclei 41 (5): 690–715. doi:10.1134/S1063779610050035. Bibcode: 2010PPN....41..690B.
Bibliography
- The Story of Spin. University of Chicago Press. 1997.
- Tuli, J. K. (2011). Nuclear Wallet Cards (8th ed.). Brookhaven National Laboratory. http://www.nndc.bnl.gov/wallet/wall35.pdf.
External links
 The Live Chart of Nuclides - IAEA with filter on decay type
The Live Chart of Nuclides - IAEA with filter on decay type- Beta decay simulation [1]
 |