Physics:Emission theory

From HandWiki

Emission theory, also called emitter theory or ballistic theory of light, was a competing theory for the special theory of relativity, explaining the results of the Michelson–Morley experiment of 1887. Emission theories obey the principle of relativity by having no preferred frame for light transmission, but say that light is emitted at speed "c" relative to its source instead of applying the invariance postulate. Thus, emitter theory combines electrodynamics and mechanics with a simple Newtonian theory. Although there are still proponents of this theory outside the scientific mainstream, this theory is considered to be conclusively discredited by most scientists.[1][2]

History

Main page: Physics:Ritz ballistic theory

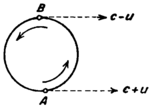
The name most often associated with emission theory is Isaac Newton. In his corpuscular theory Newton visualized light "corpuscles" being thrown off from hot bodies at a nominal speed of c with respect to the emitting object, and obeying the usual laws of Newtonian mechanics, and we then expect light to be moving towards us with a speed that is offset by the speed of the distant emitter (c ± v).

In the 20th century, special relativity was created by Albert Einstein to solve the apparent conflict between electrodynamics and the principle of relativity. The theory's geometrical simplicity was persuasive, and the majority of scientists accepted relativity by 1911. However, a few scientists rejected the second basic postulate of relativity: the constancy of the speed of light in all inertial frames. So different types of emission theories were proposed where the speed of light depends on the velocity of the source, and the Galilean transformation is used instead of the Lorentz transformation. All of them can explain the negative outcome of the Michelson–Morley experiment, since the speed of light is constant with respect to the interferometer in all frames of reference. Some of those theories were:[1][3]

  • Light retains throughout its whole path the component of velocity which it obtained from its original moving source, and after reflection light spreads out in spherical form around a center which moves with the same velocity as the original source. (Proposed by Walter Ritz in 1908).[4] This model was considered to be the most complete emission theory. (Actually, Ritz was modeling Maxwell–Lorentz electrodynamics. In a later paper [5] Ritz said that the emission particles in his theory should suffer interactions with charges along their path and thus waves (produced by them) would not retain their original emission velocities indefinitely.)
  • The excited portion of a reflecting mirror acts as a new source of light and the reflected light has the same velocity c with respect to the mirror as has original light with respect to its source. (Proposed by Richard Chase Tolman in 1910, although he was a supporter of special relativity).[6]
  • Light reflected from a mirror acquires a component of velocity equal to the velocity of the mirror image of the original source (Proposed by Oscar M. Stewart in 1911).[7]
  • A modification of the Ritz–Tolman theory was introduced by J. G. Fox (1965). He argued that the extinction theorem (i.e., the regeneration of light within the traversed medium) must be considered. In air, the extinction distance would be only 0.2 cm, that is, after traversing this distance the speed of light would be constant with respect to the medium, not to the initial light source. (Fox himself was, however, a supporter of special relativity.)[1]

Albert Einstein is supposed to have worked on his own emission theory before abandoning it in favor of his special theory of relativity. Many years later R.S. Shankland reports Einstein as saying that Ritz's theory had been "very bad" in places and that he himself had eventually discarded emission theory because he could think of no form of differential equations that described it, since it leads to the waves of light becoming "all mixed up".[8][9][10]

Refutations of emission theory

The following scheme was introduced by de Sitter[11] to test emission theories:

[math]\displaystyle{ c'=c\pm kv\, }[/math]

where c is the speed of light, v that of the source, c' the resultant speed of light, and k a constant denoting the extent of source dependence which can attain values between 0 and 1. According to special relativity and the stationary aether, k=0, while emission theories allow values up to 1. Numerous terrestrial experiments have been performed, over very short distances, where no "light dragging" or extinction effects could come into play, and again the results confirm that light speed is independent of the speed of the source, conclusively ruling out emission theories.

Astronomical sources

de Sitter's argument against emission theory.
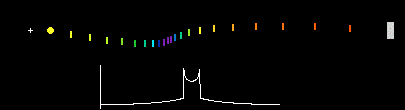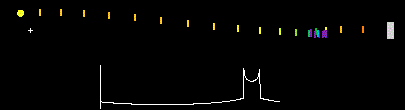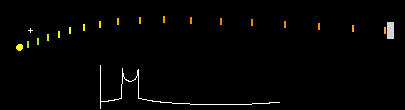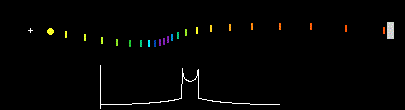
Animation of de Sitter's argument.
Willem de Sitter's argument against emission theory. According to simple emission theory, light moves at a speed of c with respect to the emitting object. If this were true, light emitted from a star in a double-star system from different parts of the orbital path would travel towards us at different speeds. For certain combinations of orbital speed, distance, and inclination, the "fast" light given off during approach would overtake "slow" light emitted during a recessional part of the star's orbit. Many bizarre effects would be seen, including (a) as illustrated, unusually shaped variable star light curves such as have never been seen, (b) extreme Doppler red- and blue-shifts in phase with the light curves, implying highly non-Keplerian orbits, and (c) splitting of the spectral lines (note simultaneous arrival of blue- and red-shifted light at the target).[12]

In 1910 Daniel Frost Comstock and in 1913 Willem de Sitter wrote that for the case of a double-star system seen edge-on, light from the approaching star might be expected to travel faster than light from its receding companion, and overtake it. If the distance was great enough for an approaching star's "fast" signal to catch up with and overtake the "slow" light that it had emitted earlier when it was receding, then the image of the star system should appear completely scrambled. De Sitter argued that none of the star systems he had studied showed the extreme optical effect behavior, and this was considered the death knell for Ritzian theory and emission theory in general, with [math]\displaystyle{ k \lt 2\times10^{-3} }[/math].[11][13][14]

The effect of extinction on de Sitter's experiment has been considered in detail by Fox, and it arguably undermines the cogency of de Sitter type evidence based on binary stars. However, similar observations have been made more recently in the x-ray spectrum by Brecher (1977), which have a long enough extinction distance that it should not affect the results. The observations confirm that the speed of light is independent of the speed of the source, with [math]\displaystyle{ k \lt 2\times10^{-9} }[/math].[2]

Hans Thirring argued in 1924, that an atom which is accelerated during the emission process by thermal collisions in the sun, is emitting light rays having different velocities at their start- and endpoints. So one end of the light ray would overtake the preceding parts, and consequently the distance between the ends would be elongated up to 500 km until they reach Earth, so that the mere existence of sharp spectral lines in the sun's radiation, disproves the ballistic model.[15]

Terrestrial sources

Such experiments include that of Sadeh (1963) who used a time-of-flight technique to measure velocity differences of photons traveling in opposite direction, which were produced by positron annihilation.[16] Another experiment was conducted by Alväger et al. (1963), who compared the time of flight of gamma rays from moving and resting sources.[17] Both experiments found no difference, in accordance with relativity.

Filippas and Fox (1964)[18] did not consider Sadeh (1963) and Alväger (1963) to have sufficiently controlled for the effects of extinction. So they conducted an experiment using a setup specifically designed to account for extinction. Data collected from various detector-target distances were consistent with there being no dependence of the speed of light on the velocity of the source, and were inconsistent with modeled behavior assuming c ± v both with and without extinction.

Continuing their previous investigations, Alväger et al. (1964) observed π0-mesons which decay into photons at 99.9% light speed. The experiment showed that the photons didn't attain the velocity of their sources and still traveled at the speed of light, with [math]\displaystyle{ k =(-3\pm13)\times10^{-5} }[/math]. The investigation of the media which were crossed by the photons showed that the extinction shift was not sufficient to distort the result significantly.[19]

Also measurements of neutrino speed have been conducted. Mesons travelling nearly at light speed were used as sources. Since neutrinos only participate in the electroweak interaction, extinction plays no role. Terrestrial measurements provided upper limits of [math]\displaystyle{ k\leq10^{-6} }[/math].

Interferometry

The Sagnac effect demonstrates that one beam on a rotating platform covers less distance than the other beam, which creates the shift in the interference pattern. Georges Sagnac's original experiment has been shown to suffer extinction effects, but since then, the Sagnac effect has also been shown to occur in vacuum, where extinction plays no role.[20][21]

The predictions of Ritz's version of emission theory were consistent with almost all terrestrial interferometric tests save those involving the propagation of light in moving media, and Ritz did not consider the difficulties presented by tests such as the Fizeau experiment to be insurmountable. Tolman, however, noted that a Michelson–Morley experiment using an extraterrestrial light source could provide a decisive test of the Ritz hypothesis. In 1924, Rudolf Tomaschek performed a modified Michelson–Morley experiment using starlight, while Dayton Miller used sunlight. Both experiments were inconsistent with the Ritz hypothesis.[22]

Babcock and Bergman (1964) placed rotating glass plates between the mirrors of a common-path interferometer set up in a static Sagnac configuration. If the glass plates behave as new sources of light so that the total speed of light emerging from their surfaces is c + v, a shift in the interference pattern would be expected. However, there was no such effect which again confirms special relativity, and which again demonstrates the source independence of light speed. This experiment was executed in vacuum, thus extinction effects should play no role.[23]

Albert Abraham Michelson (1913) and Quirino Majorana (1918/9) conducted interferometer experiments with resting sources and moving mirrors (and vice versa), and showed that there is no source dependence of light speed in air. Michelson's arrangement was designed to distinguish between three possible interactions of moving mirrors with light: (1) "the light corpuscles are reflected as projectiles from an elastic wall", (2) "the mirror surface acts as a new source", (3) "the velocity of light is independent of the velocity of the source". His results were consistent with source independence of light speed.[24] Majorana analyzed the light from moving sources and mirrors using an unequal arm Michelson interferometer that was extremely sensitive to wavelength changes. Emission theory asserts that Doppler shifting of light from a moving source represents a frequency shift with no shift in wavelength. Instead, Majorana detected wavelength changes inconsistent with emission theory.[25][26]

Beckmann and Mandics (1965)[27] repeated the Michelson (1913) and Majorana (1918) moving mirror experiments in high vacuum, finding k to be less than 0.09. Although the vacuum employed was insufficient to definitively rule out extinction as the reason for their negative results, it was sufficient to make extinction highly unlikely. Light from the moving mirror passed through a Lloyd interferometer, part of the beam traveling a direct path to the photographic film, part reflecting off the Lloyd mirror. The experiment compared the speed of light hypothetically traveling at c + v from the moving mirrors, versus reflected light hypothetically traveling at c from the Lloyd mirror.

Other refutations

Emission theories use the Galilean transformation, according to which time coordinates are invariant when changing frames ("absolute time"). Thus the Ives–Stilwell experiment, which confirms relativistic time dilation, also refutes the emission theory of light. As shown by Howard Percy Robertson, the complete Lorentz transformation can be derived, when the Ives–Stillwell experiment is considered together with the Michelson–Morley experiment and the Kennedy–Thorndike experiment.[28]

Furthermore, quantum electrodynamics places the propagation of light in an entirely different, but still relativistic, context, which is completely incompatible with any theory that postulates a speed of light that is affected by the speed of the source.

See also

References

  1. ↑ 1.0 1.1 1.2 Fox, J. G. (1965), "Evidence Against Emission Theories", American Journal of Physics 33 (1): 1–17, doi:10.1119/1.1971219, Bibcode: 1965AmJPh..33....1F. 
  2. ↑ 2.0 2.1 Brecher, K. (1977), "Is the speed of light independent of the velocity of the source", Physical Review Letters 39 (17): 1051–1054, doi:10.1103/PhysRevLett.39.1051, Bibcode: 1977PhRvL..39.1051B. 
  3. ↑ Tolman, Richard Chace (1912), "Some Emission Theories of Light", Physical Review 35 (2): 136–143, doi:10.1103/physrevseriesi.35.136, Bibcode: 1912PhRvI..35..136T, http://authors.library.caltech.edu/6213/1/TOLpr12.pdf 
  4. ↑ Ritz, Walter (1908), "Recherches critiques sur l'Électrodynamique Générale", Annales de Chimie et de Physique 13: 145–275, Bibcode: 1908AChPh..13..145R, http://gallica.bnf.fr/ark:/12148/bpt6k349439.image.f143 . See also the English translation .
  5. ↑ Ritz,Walther (1908), "Recherches Critiques sur les Theories Electrodynamiques de Cl. Maxwell et de H.-A. Lorentz", Archives des sciences physiques et naturelles 36: 209, http://www.datasync.com/~rsf1/rtz-mir.htm 
  6. ↑ Tolman, Richard Chace (1910), "The Second Postulate of Relativity", Physical Review 31 (1): 26–40, doi:10.1103/physrevseriesi.31.26, Bibcode: 1910PhRvI..31...26T 
  7. ↑ Stewart, Oscar M. (1911), "The Second Postulate of Relativity and the Electromagnetic Emission Theory of Light", Physical Review 32 (4): 418–428, doi:10.1103/physrevseriesi.32.418, Bibcode: 1911PhRvI..32..418S, https://zenodo.org/record/1432478 
  8. ↑ Shankland, R. S. (1963), "Conversations with Albert Einstein", American Journal of Physics 31 (1): 47–57, doi:10.1119/1.1969236, Bibcode: 1963AmJPh..31...47S 
  9. ↑ Norton, John D., John D. (2004), "Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905", Archive for History of Exact Sciences 59 (1): 45–105, doi:10.1007/s00407-004-0085-6, Bibcode: 2004AHES...59...45N, http://philsci-archive.pitt.edu/archive/00001743/ 
  10. ↑ Martínez, Alberto A. (2004), "Ritz, Einstein, and the Emission Hypothesis", Physics in Perspective 6 (1): 4–28, doi:10.1007/s00016-003-0195-6, Bibcode: 2004PhP.....6....4M 
  11. ↑ 11.0 11.1 De Sitter, Willem (1913), "On the constancy of the velocity of light", Proceedings of the Royal Netherlands Academy of Arts and Sciences 16 (1): 395–396 
  12. ↑ Bergmann, Peter (1976). Introduction to the Theory of Relativity. Dover Publications, Inc. pp. 19–20. ISBN 0-486-63282-2. https://archive.org/details/introductiontoth00berg/page/19. "In some cases, we should observe the same component of the double star system simultaneously at different places, and these 'ghost stars' would disappear and reappear in the course of their periodic motions." 
  13. ↑ Comstock, Daniel Frost (1910), "A Neglected Type of Relativity", Physical Review 30 (2): 267, doi:10.1103/PhysRevSeriesI.30.262, Bibcode: 1910PhRvI..30..262. 
  14. ↑ De Sitter, Willem (1913), "A proof of the constancy of the velocity of light", Proceedings of the Royal Netherlands Academy of Arts and Sciences 15 (2): 1297–1298, Bibcode: 1913KNAB...15.1297D 
  15. ↑ Thirring, Hans (1924), "Über die empirische Grundlage des Prinzips der Konstanz der Lichtgeschwindigkeit", Zeitschrift für Physik 31 (1): 133–138, doi:10.1007/BF02980567, Bibcode: 1925ZPhy...31..133T. 
  16. ↑ Sadeh, D. (1963). "Experimental Evidence for the Constancy of the Velocity of Gamma Rays, Using Annihilation in Flight". Physical Review Letters 10 (7): 271–273. doi:10.1103/PhysRevLett.10.271. Bibcode: 1963PhRvL..10..271S. 
  17. ↑ Alväger, T.; Nilsson, A.; Kjellman, J. (1963). "A Direct Terrestrial Test of the Second Postulate of Special Relativity". Nature 197 (4873): 1191. doi:10.1038/1971191a0. Bibcode: 1963Natur.197.1191A. 
  18. ↑ Filippas, T.A.; Fox, J.G. (1964). "Velocity of Gamma Rays from a Moving Source". Physical Review 135 (4B): B1071-1075. doi:10.1103/PhysRev.135.B1071. Bibcode: 1964PhRv..135.1071F. 
  19. ↑ Alväger, T.; Farley, F. J. M.; Kjellman, J.; Wallin, L. (1964), "Test of the second postulate of special relativity in the GeV region", Physics Letters 12 (3): 260–262, doi:10.1016/0031-9163(64)91095-9, Bibcode: 1964PhL....12..260A. 
  20. ↑ Sagnac, Georges (1913), "L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en rotation uniforme", Comptes Rendus 157: 708–710 
  21. ↑ Sagnac, Georges (1913), "Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant", Comptes Rendus 157: 1410–1413 
  22. ↑ Martínez, A.A. (2004). "Ritz, Einstein, and the Emission Hypothesis". Physics in Perspective 6 (1): 4–28. doi:10.1007/s00016-003-0195-6. Bibcode: 2004PhP.....6....4M. https://webspace.utexas.edu/aam829/1/m/Relativity_files/RitzEinstein.pdf. Retrieved 24 April 2012. 
  23. ↑ Babcock, G. C.; Bergman, T. G. (1964), "Determination of the Constancy of the Speed of Light", Journal of the Optical Society of America 54 (2): 147–150, doi:10.1364/JOSA.54.000147, Bibcode: 1964JOSA...54..147B 
  24. ↑ Michelson, A.A. (1913). "Effect of Reflection from a Moving Mirror on the Velocity of Light". Astrophysical Journal 37: 190–193. doi:10.1086/141987. Bibcode: 1913ApJ....37..190M. 
  25. ↑ Majorana, Q. (1918). "On the Second Postulate of the Theory of Relativity: Experimental Demonstration of the Constancy of Velocity of the Light reflected from a Moving Mirror". Philosophical Magazine 35 (206): 163–174. doi:10.1080/14786440208635748. 
  26. ↑ Majorana, Q. (1919). "Experimental Demonstration of the Constancy of Velocity of the Light emitted by a Moving Source". Philosophical Magazine 37 (217): 145–150. doi:10.1080/14786440108635871. 
  27. ↑ Beckmann, P.; Mandics, P. (1965). "Test of the Constancy of the Velocity of Electromagnetic Radiation in High Vacuum". Journal of Research of the National Bureau of Standards Section D 69D (4): 623–628. doi:10.6028/jres.069d.071. 
  28. ↑ Robertson, H. P. (1949). "Postulate versus Observation in the Special Theory of Relativity". Reviews of Modern Physics 21 (3): 378–382. doi:10.1103/RevModPhys.21.378. Bibcode: 1949RvMP...21..378R. 

External links




Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Emission_theory&oldid=3281023"