Physics:Ives–Stilwell experiment

From HandWiki
Figure 1. Ives–Stilwell experiment (1938). "Canal rays" (a mixture of mostly H2+ and H3+ ions) were accelerated through perforated plates charged from 6,788 to 18,350 volts. The beam and its reflected image were simultaneously observed with the aid of a concave mirror offset 7° from the beam.[1]
Figure 2. The dispersing element of the spectrograph was a diffraction grating blazed to maximize the amount of the total light thrown into the first order. A high quality telescope lens of five foot focal length collimated the light from the slit into a parallel beam onto the grating, and the diffracted light was then focused by a similar lens onto a photographic plate. The entire apparatus was mounted on a stable platform and conducted in a constant temperature room regulated to 0.1°C.

The Ives–Stilwell experiment tested the contribution of relativistic time dilation to the Doppler shift of light.[1][2] The result was in agreement with the formula for the transverse Doppler effect and was the first direct, quantitative confirmation of the time dilation factor. Since then many Ives–Stilwell type experiments have been performed with increased precision. Together with the Michelson–Morley and Kennedy–Thorndike experiments it forms one of the fundamental tests of special relativity theory.[3] Other tests confirming the relativistic Doppler effect are the Mössbauer rotor experiment and modern Ives–Stilwell experiments.

Both time dilation and the relativistic Doppler effect were predicted by Albert Einstein in his seminal 1905 paper.[4] Einstein subsequently (1907) suggested an experiment based on the measurement of the relative frequencies of light perceived as arriving from "canal rays" (positive ion beams created by certain types of gas-discharge tubes) in motion with respect to the observer, and he calculated the additional Doppler shift due to time dilation.[5] This effect was later called "transverse Doppler effect" (TDE), since such experiments were initially imagined to be conducted at right angles with respect to the moving source, in order to avoid the influence of the longitudinal Doppler shift. Eventually, Herbert E. Ives and G. R. Stilwell (referring to time dilation as following from the theory of Lorentz and Larmor) gave up the idea of measuring this effect at right angles. They used rays in longitudinal direction and found a way to separate the much smaller TDE from the much bigger longitudinal Doppler effect. The experiment was performed in 1938[1] and was reprised several times.[2] Similar experiments were conducted several times with increased precision, for example, by Otting (1939),[6] Mandelberg et al. (1962),[7] Hasselkamp et al. (1979),[8] and Botermann et al.[9]

Experiments with "canal rays"

Experimental challenges

Initial attempts to measure the second order transverse Doppler effect in canal rays completely failed. For example, Stark's 1906 measurements showed systematic errors ten times the predicted effect.[5] The maximum speed achievable in early gas-discharge tubes was about 0.005 c, which implied a transverse Doppler shift of only about 1.25×10−5. The small TDE achievable was considerably less than the width of the emission lines, which were relatively diffuse due to the Doppler line-broadening resulting from non-uniformity of ion speeds.

By the 1930s, improvements in canal-ray tubes allowed for considerable sharpening of the emission lines.[1] Even with these improvements, however, performing the experiment as usually imagined (with the observation being made at right angles to the beam) would be extremely difficult since small errors in the angle of observation would result in line-shifts of magnitude comparable to the magnitude of the anticipated effect.[1]

Figure 3. Why it is difficult to measure the transverse Doppler effect accurately using a transverse beam. The illustration shows the results of attempting to measure the 4861 ångström line emitted by a beam of "canal rays" as they recombine with electrons stripped from the dilute hydrogen gas used to fill the canal ray tube. With v = 0.005 c, the predicted result of the TDE would be a 4861.06 ångström line. On the left, conventional Doppler shift results in broadening the emission line to such an extent that the TDE cannot be observed. In the middle, we see that even if one narrows one's view to the exact center of the beam, very small deviations of the beam from an exact right angle introduce shifts comparable to the predicted effect. Ives and Stilwell used a concave mirror that allowed them to simultaneously observe a nearly longitudinal direct beam (blue) and its reflected image (red). Spectroscopically, three lines would be observed: An undisplaced emission line, and blueshifted and redshifted lines. The average of the redshifted and blueshifted lines was compared with the undisplaced line.

To avoid the issues associated with observing the beam at right angles, Ives and Stilwell used a small mirror within the canal ray tube (See Fig. 1 and Fig. 3) to observe the beam simultaneously in two directions both with and against the motions of the particles. The TDE would manifest itself as a shift of the center of gravity of the simultaneously red- and blue-shifted spectral lines.[1]

Theory

In 1937, Ives performed a detailed analysis of the spectral shifts to be expected of particle beams observed at different angles following a "test theory" which was consistent with the Michelson-Morley experiment (MMX) and the Kennedy-Thorndike experiment (KTX), but which differed from special relativity (and the mathematically equivalent theory of Lorentz and Lamor) in including a parameter [math]\displaystyle{ n }[/math] whose value can not be determined by MMX and KTX alone.[10] Various values of [math]\displaystyle{ n }[/math] would correspond to various combinations of length contraction, width expansion, and time dilation, where [math]\displaystyle{ n=1 }[/math] would be the value predicted by special relativity. Ives proposed the optical experiment described in this article to determine the precise value of [math]\displaystyle{ n. }[/math][10]

We will not present Ives' 1937 analysis, but instead will compare the predictions of special relativity against the predictions of "classical" aether theory with the apparatus stationary in the hypothetical aether, even though the classical aether had already long been ruled out by MMX and KTX.[11][12]

Classical analysis

In the classical Doppler effect, the wavelength of light observed by a stationary observer of light emitted by a source moving at speed [math]\displaystyle{ v }[/math] away from or towards the observer is given by

[math]\displaystyle{ \lambda_{obs} = \lambda \cdot ( 1 \pm \beta) }[/math] where [math]\displaystyle{ \beta = v/c }[/math]

The top sign is used if the source is receding, and the bottom sign if it is approaching the observer.

  • We note that the magnitude of the wavelength shift for the source moving away from the observer exactly equals the magnitude of the wavelength shift for the source moving towards the observer
  • The average of the observed wavelengths for a source moving away from the observer and the source moving towards the observer at the same speed exactly equals the wavelength of the source.[11]

Relativistic analysis

In the relativistic longitudinal Doppler effect, the observed wavelength with source and observer moving away from each other at speed [math]\displaystyle{ v }[/math] is given by

[math]\displaystyle{ \lambda_{obs} = \lambda \cdot \frac{ \sqrt{ 1 + \beta } } {\sqrt { 1 - \beta} } \,\, }[/math] where [math]\displaystyle{ \beta = v/c }[/math]

The signs will be reversed with the source and observer moving towards each other. In the Ives and Stilwell experiment, the direct view of the particle beam will be blueshifted, while the reflected view of the particle beam will be redshifted.

The first few terms of the Taylor series expansion for the direct view of the particle beam is given by

[math]\displaystyle{ \lambda_{obs} = \lambda \cdot \left( 1 - \beta + \frac{\beta^2}{2} - \frac{\beta^3}{2} + \frac{3\beta^4}{8} \ldots \right) }[/math]

while the first few terms of the Taylor series expansion for the reflected view of the particle beam is given by

[math]\displaystyle{ \lambda_{obs} = \lambda \cdot \left(1 + \beta + \frac{\beta^2}{2} + \frac{\beta^3}{2} + \frac{3\beta^4}{8} \ldots \right) }[/math]

The even power terms have the same sign for both views, meaning that both the direct and reflected rays will show an increase in wavelength over that predicted by the classical Doppler analysis.[11][12]

The average of the direct and reflected wavelengths is given by

[math]\displaystyle{ \lambda_{avg} = \lambda \cdot \left( 1 + \frac{\beta^2}{2} + \frac{3\beta^4}{8} \ldots \right) = }[/math] [math]\displaystyle{ \frac{\lambda}{\sqrt{1-\beta^2}} = \gamma \cdot \lambda }[/math]

where [math]\displaystyle{ \gamma }[/math] is the Lorentz factor. Special relativity therefore predicts that the center of gravity of Doppler-shifted emission lines emitted by a source moving towards an observer and its reflected image moving away from the observer will be offset from unshifted emission lines by an amount equal to the transverse Doppler effect.[11][12]

The experiment of 1938

Figure 4. Doppler-shifted Balmer line [math]\displaystyle{ H_\beta }[/math] from the Ives-Stilwell experiment

In the experiment, Ives and Stilwell used hydrogen discharge tubes as the source of canal rays which consisted primarily of positive H2+ and H3+ ions. (Free H+ ions were present in too small an amount to be usable, since they quickly combined with H2 molecules to form H3+ ions.) These ions, after being accelerated to high speed in the canal ray tube, would interact with molecules of the fill gas (which sometimes included other gases than H2) to release excited atomic hydrogen atoms whose velocities were determined by the charge-to-mass ratios of the parent H2+ and H3+ ions.[12] The excited atomic hydrogen atoms emitted bright emission lines. For their paper, Ives and Stilwell focused on the blue-green 4861 Å [math]\displaystyle{ H_\beta }[/math] line of the Balmer series. Fig. 4 shows an example of the results that they obtained, with an undisplaced emission line in the center, and lines from Doppler-shifted atomic hydrogen released from H2+ and H3+ ions at three different voltages on either side of the center line. The particle velocities, as measured by the first-order Doppler displacements, were consistently within 1% of the values computed by the theoretical relationship [math]\displaystyle{ eE = M(v^2/c^2)/2, }[/math] where e is the charge on the hydrogen atom, E is the voltage between the electrode plates, and M is the mass of the observed particle.[1]

The asymmetry of the Doppler-shifted lines with respect to the undisplaced central emission line is not evident to casual inspection, but requires extreme precision of measurement with careful attention to sources of systematic error. In their optical arrangement, illustrated in Fig. 2, the first order (classical Doppler) displacement of emissions from H2+ ions at 20,000 volts was about 2 mm. The expected second order shift of the center of gravity of direct and reflected views of the emissions was only about 0.005 mm which corresponded to 0.05 Å, requiring measurement accuracies of several tenths of a micron.[1]

Figure 5. Hβ emission lines and H2 molecular absorption lines in the Ives-Stilwell experiment

Initial measurements of the displacements were very erratic. The source of the unsystematic errors in measurement of the center of gravity of the displaced lines was found to be due to the complex molecular absorption spectrum of the fill gas. An emission line, passing adjacent to a molecular absorption line of the fill gas, would be differentially absorbed on one side or the other of its nominal center, and the measurement of its wavelength would thus be disturbed. Fig. 5 illustrates the issue. Fig. 5A illustrates an undisplaced [math]\displaystyle{ H_\beta }[/math] emission line. Fig. 5B illustrates the molecular absorption spectrum of the fill gas, obtained by photographing the spectrum of the arc behind the electrode of the canal ray tube (see Fig. 1). Fig. 5C illustrates an undisplaced [math]\displaystyle{ H_\beta }[/math] emission line surrounded by displaced [math]\displaystyle{ H_\beta }[/math] emission lines from H2+ and H3+. At the particular voltage chosen, the lines from H2+ are clear of the molecular absorption lines (see arrows), but the lines from H3+ are not.[1]

Figure 6. Computed and observed second-order shifts plotted against first-order Doppler shifts

As a result of this issue, the number of voltages available yielding direct and reflected lines in clear spaces was relatively limited.[1]

Ives and Stilwell compared their results against theoretical expectation using several approaches. Fig. 6 compares theoretical versus measured center-of-gravity shifts [math]\displaystyle{ \Delta\lambda_2 }[/math] plotted against the emission lines' first-order Doppler shifts [math]\displaystyle{ \Delta\lambda_1. }[/math] The advantage of this method over the other method presented in their paper (plotting center-of-gravity shifts against the computed velocity, based on voltage) is that it was independent of any errors of voltage measurement and did not require any assumptions of the voltage-velocity relationship.[1]

In terms of Ives' 1937 test theory,[10] the close agreement between the observed center-of-gravity displacements versus theoretical expectation support [math]\displaystyle{ n=1, }[/math] which corresponds to length contraction by the Lorentz factor [math]\displaystyle{ \lambda }[/math] in the direction of motion, no length changes at right angles to the motion, and time dilation by the Lorentz factor.[1] The results therefore validated a key prediction of the theory of relativity, although it might be noted that Ives himself preferred to interpret the results in terms of the obsolescent theory of Lorentz and Lamor.[12]

The experiment of 1941

In the 1938 experiment, the maximum TDE was limited to 0.047 Å. The chief difficulty that Ives and Stilwell encountered in attempts to achieve larger shifts was that when they raised the electric potential between the accelerating electrodes to above 20,000 volts, breakdown and sparking would occur that could lead to destruction of the tube.

This difficulty was overcome by using multiple electrodes. Using a four-electrode version of the canal ray tube with three gaps, a total potential difference of 43,000 volts could be achieved. A voltage drop of 5,000 volts was used across the first gap, while the remaining voltage drop was distributed between the second and third gaps. With this tube, a highest shift of 0.11 Å was achieved for H2+ ions.[2]

Other aspects of the experiment were also improved. Careful tests showed that the "undisplaced" particles yielding the central line actually acquired a small velocity imparted to them in the same direction of motion as the moving particles (no more than about 750 meters per second). Under normal circumstances, this would be of no consequence, since this effect would only result in a slight apparent broadening of the direct and reflected images of the central line. But if the mirror were tarnished, the central line might be expected to shift slightly, since the redshifted reflected view of the emission line would contribute less to the measured wavelength than the blueshifted direct view. Other controls were performed to address various objections of critics of the original experiment.

The net result of all of this attention to detail was the complete verification of Ives and Stilwell's 1938 results and the extension of these results to higher speeds.[2]

Mössbauer rotor experiments

The Kündig experiment (1963). An 57Fe Mössbauer absorber was mounted 9.3 cm from the axis of an ultracentrifuge rotor. A 57Co source was mounted on a piezoelectric transducer (PZT) at the rotor center. Spinning the rotor caused the source and absorber to fall out of resonance. A modulated voltage applied to the transducer set the source in radial motion relative to the absorber, so that the amount of conventional Doppler shift that would restore resonance could be measured. For example, withdrawing the source at 195 μm/s produced a conventional Doppler redshift equivalent to the TDE resulting from spinning the absorber at 35,000 rpm.

Relativistic Doppler effect

A more precise confirmation of the relativistic Doppler effect was achieved by the Mössbauer rotor experiments. From a source in the middle of a rotating disk, gamma rays are sent to an absorber at the rim (in some variations this scheme was reversed), and a stationary counter was placed beyond the absorber. According to relativity, the characteristic resonance absorption frequency of the moving absorber at the rim should decrease due to time dilation, so the transmission of gamma rays through the absorber increases, which is subsequently measured by the stationary counter beyond the absorber. This effect was actually observed using the Mössbauer effect. The maximal deviation from time dilation was 10−5, thus the precision was much higher than that (10−2) of the Ives–Stilwell experiments. Such experiments were performed by Hay et al. (1960),[13] Champeney et al. (1963, 1965),[14][15] and Kündig (1963).[16]

Isotropy of the speed of light

Mössbauer rotor experiments were also used to measure a possible anisotropy of the speed of light. That is, a possible aether wind should exert a disturbing influence on the absorption frequency. However, as in all other aether drift experiments (Michelson–Morley experiment), the result was negative, putting an upper limit to aether drift of 2.0 cm/s. Experiments of that kind were performed by Champeney and Moon (1961),[17] Champeney et al. (1963),[18] Turner and Hill (1964),[19] and Preikschat supervised by Isaak (1968).[20]

Modern experiments

Further information: Physics:Modern searches for Lorentz violation

Fast moving clocks

A considerably higher precision has been achieved in modern variations of Ives–Stilwell experiments. In heavy-ion storage rings, as the TSR at the MPIK or ESR at the GSI Helmholtz Centre for Heavy Ion Research, the Doppler shift of lithium ions traveling at high speed [21] is evaluated by using saturated spectroscopy or optical–optical double resonance.

Schematic view of an optical optical double-resonance spectroscopy with the transition frequencies [math]\displaystyle{ \nu_1 }[/math] and [math]\displaystyle{ \nu_2 }[/math] of a moving ion and counter-propagating laser beams with the frequencies [math]\displaystyle{ \nu_a }[/math] and [math]\displaystyle{ \nu_p }[/math].
Schematic view of saturation spectroscopy with the transition frequencies [math]\displaystyle{ \nu_0 }[/math] of a moving ion and counter-propagating laser beams with the frequencies [math]\displaystyle{ \nu_a }[/math] and [math]\displaystyle{ \nu_p }[/math].

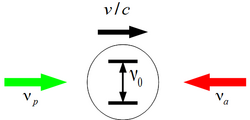
Due to their frequencies emitted, these ions can be considered as optical atomic clocks of high precision. Using the framework of Mansouri–Sexl[22] a possible deviation from special relativity can be quantified by

[math]\displaystyle{ \frac{\nu_a\nu_p}{\nu_1\nu_2} = 1 + 2\hat{\alpha}\beta^2, }[/math][dubious – discuss]

with [math]\displaystyle{ \nu_a }[/math] as frequency of the laser beam propagating anti-parallel to the ion beam and [math]\displaystyle{ \nu_p }[/math] as frequency of the laser beam propagating parallel to the ion beam. [math]\displaystyle{ \nu_1 }[/math] and [math]\displaystyle{ \nu_2 }[/math] are the transition frequencies of the transitions in rest. [math]\displaystyle{ \beta = v/c }[/math] with [math]\displaystyle{ v }[/math] as ion velocity and [math]\displaystyle{ c }[/math] as speed of light. In the case of saturation spectroscopy the formula changes to

[math]\displaystyle{ \frac{\nu_a\nu_p}{\nu_0^2} = 1 + 2\hat{\alpha}\beta^2, }[/math]

with [math]\displaystyle{ \nu_0 }[/math] as the transition frequency in rest. In the case that special relativity is valid [math]\displaystyle{ \hat{\alpha} }[/math] is equal to zero.

Author Year Speed Upper limit of [math]\displaystyle{ |\hat{\alpha}| }[/math]
Grieser et al.[23] 1994 0.064 c ≤ 8×10−7
Saathoff et al.[24] 2003 0.064 c ≤ 2×10−7
Reinhardt et al.[25] 2007 0.03 c, 0.064 c ≤ 8×10−8
Novotny et al.[26] 2009 0.338 c ≤ 1×10−6
Botermann et al.[9] 2014 0.338 c ≤ 2×10−8

Slow moving clocks

Meanwhile, the measurement of time dilation at everyday speeds has been accomplished as well. Chou et al. (2010) created two clocks each holding a single 27Al+ ion in a Paul trap. In one clock, the Al+ ion was accompanied by a 9Be+ ion as a "logic" ion, while in the other, it was accompanied by a 25Mg+ ion. The two clocks were situated in separate laboratories and connected with a 75 m long, phase-stabilized optical fiber for exchange of clock signals. These optical atomic clocks emitted frequencies in the petahertz (1 PHz = 1015 Hz) range and had frequency uncertainties in the 10−17 range. With these clocks, it was possible to measure a frequency shift due to time dilation of ∼10−16 at speeds below 36 km/h (< 10 m/s, the speed of a fast runner) by comparing the rates of moving and resting aluminum ions. It was also possible to detect gravitational time dilation from a difference in elevation between the two clocks of 33 cm.[27]

See also

References

  1. ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 Ives, H. E.; Stilwell, G. R. (1938). "An experimental study of the rate of a moving atomic clock". Journal of the Optical Society of America 28 (7): 215. doi:10.1364/JOSA.28.000215. Bibcode: 1938JOSA...28..215I. 
  2. ↑ 2.0 2.1 2.2 2.3 Ives, H. E.; Stilwell, G. R. (1941). "An experimental study of the rate of a moving atomic clock. II". Journal of the Optical Society of America 31 (5): 369. doi:10.1364/JOSA.31.000369. Bibcode: 1941JOSA...31..369I. 
  3. ↑ Robertson, H. P. (1949). "Postulate versus Observation in the Special Theory of Relativity". Reviews of Modern Physics 21 (3): 378–382. doi:10.1103/RevModPhys.21.378. Bibcode: 1949RvMP...21..378R. https://cds.cern.ch/record/1061896/files/RevModPhys.21.378.pdf. 
  4. ↑ Einstein, Albert (1905). "Zur Elektrodynamik bewegter Körper". Annalen der Physik 322 (10): 891–921. doi:10.1002/andp.19053221004. Bibcode: 1905AnP...322..891E. http://sedici.unlp.edu.ar/handle/10915/2786.  English translation: 'On the Electrodynamics of Moving Bodies'
  5. ↑ 5.0 5.1 Einstein, Albert (1907). "Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips". Annalen der Physik 328 (6): 197–198. doi:10.1002/andp.19073280613. Bibcode: 1907AnP...328..197E. http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1907_23_197-198.pdf. 
  6. ↑ Otting, G. (1939). "Der quadratische Dopplereffekt". Physikalische Zeitschrift 40: 681–687. 
  7. ↑ Mandelberg, Hirsch I.; Witten, Louis (1962). "Experimental verification of the relativistic doppler effect". Journal of the Optical Society of America 52 (5): 529. doi:10.1364/josa.52.000529. Bibcode: 1962JOSA...52..529M. 
  8. ↑ Hasselkamp, D.; Mondry, E.; Scharmann, A. (1979-06-01). "Direct observation of the transversal Doppler-shift". Zeitschrift für Physik A 289 (2): 151–155. doi:10.1007/BF01435932. Bibcode: 1979ZPhyA.289..151H. 
  9. ↑ 9.0 9.1 Botermann, Benjamin; Bing, Dennis; Geppert, Christopher; Gwinner, Gerald; Hänsch, Theodor W.; Huber, Gerhard; Karpuk, Sergei; Krieger, Andreas et al. (September 2014). "Test of Time Dilation Using Stored Li+ Ions as Clocks at Relativistic Speed". Physical Review Letters 113 (12): 120405. doi:10.1103/PhysRevLett.113.120405. PMID 25279611. Bibcode: 2014PhRvL.113l0405B. 
  10. ↑ 10.0 10.1 10.2 Ives, Herbert E. (1937). "The Doppler Effect Considered in Relation to the Michelson-Morley Experiment". Journal of the Optical Society of America 27 (11): 389–392. doi:10.1364/JOSA.27.000389. 
  11. ↑ 11.0 11.1 11.2 11.3 Richmond, Michael. "The Relativistic Doppler Effect". Rochester Institute of Technology. http://spiff.rit.edu/classes/phys314/lectures/doppler/doppler.html. 
  12. ↑ 12.0 12.1 12.2 12.3 12.4 French, A. P. (1968). Special Relativity. New York: W. W. Norton & Company, Inc.. pp. 144–146. ISBN 0-393-09793-5. 
  13. ↑ Hay, H. J.; Schiffer, J. P.; Cranshaw, T. E.; Egelstaff, P. A. (1960). "Measurement of the Red Shift in an Accelerated System Using the Mössbauer Effect in 57Fe". Physical Review Letters 4 (4): 165–166. doi:10.1103/PhysRevLett.4.165. Bibcode: 1960PhRvL...4..165H. 
  14. ↑ Champeney, D. C.; Isaak, G. R.; Khan, A. M. (1963). "Measurement of Relativistic Time Dilatation using the Mössbauer Effect". Nature 198 (4886): 1186–1187. doi:10.1038/1981186b0. Bibcode: 1963Natur.198R1186C. 
  15. ↑ Champeney, D. C.; Isaak, G. R.; Khan, A. M. (1965). "A time dilatation experiment based on the Mössbauer effect". Proceedings of the Physical Society 85 (3): 583–593. doi:10.1088/0370-1328/85/3/317. Bibcode: 1965PPS....85..583C. 
  16. ↑ Kündig, Walter (1963). "Measurement of the Transverse Doppler Effect in an Accelerated System". Physical Review 129 (6): 2371–2375. doi:10.1103/PhysRev.129.2371. Bibcode: 1963PhRv..129.2371K. 
  17. ↑ Champeney, D. C.; Moon, P. B. (1961). "Absence of Doppler Shift for Gamma Ray Source and Detector on Same Circular Orbit". Proceedings of the Physical Society 77 (2): 350–352. doi:10.1088/0370-1328/77/2/318. Bibcode: 1961PPS....77..350C. 
  18. ↑ Champeney, D. C.; Isaak, G. R.; Khan, A. M. (1963). "An 'aether drift' experiment based on the Mössbauer effect". Physics Letters 7 (4): 241–243. doi:10.1016/0031-9163(63)90312-3. Bibcode: 1963PhL.....7..241C. 
  19. ↑ Turner, K. C.; Hill, H. A. (1964). "New Experimental Limit on Velocity-Dependent Interactions of Clocks and Distant Matter". Physical Review 134 (1B): 252–256. doi:10.1103/PhysRev.134.B252. Bibcode: 1964PhRv..134..252T. 
  20. ↑ Preikschat, E. (1968). The Mössbauer effect and tests of relativity (PhD). University of Birmingham. Retrieved November 12, 2018.
  21. ↑ "Lithium Experiment SRT GSI". https://www.youtube.com/watch?v=2NsnX_omxMA. 
  22. ↑ Mansouri, R.; Sexl, R. U. (1977). "A test theory of special relativity I–III". Gen. Rel. Grav. 8 (7): 497, 515, 809. doi:10.1007/BF00762634. Bibcode: 1977GReGr...8..497M. 
  23. ↑ Grieser, R.; Klein, R.; Huber, G.; Dickopf, S.; Klaft, I.; Knobloch, P.; Merz, P.; Albrecht, F. et al. (1994). "A test of special relativity with stored lithium ions". Applied Physics B: Lasers and Optics 59 (2): 127–133. doi:10.1007/BF01081163. Bibcode: 1994ApPhB..59..127G. https://cds.cern.ch/record/258041. 
  24. ↑ Saathoff, G.; Karpuk, S.; Eisenbarth, U.; Huber, G.; Krohn, S.; Horta, R. Muñoz; Reinhardt, S.; Schwalm, D. et al. (2003). "Improved Test of Time Dilation in Special Relativity". Phys. Rev. Lett. 91 (19): 190403. doi:10.1103/PhysRevLett.91.190403. PMID 14611572. Bibcode: 2003PhRvL..91s0403S. 
  25. ↑ Reinhardt, S.; Saathoff, G.; Buhr, H.; Carlson, L. A.; Wolf, A.; Schwalm, D.; Karpuk, S.; Novotny, C. et al. (2007). "Test of relativistic time dilation with fast optical atomic clocks at different velocities". Nature Physics 3 (12): 861–864. doi:10.1038/nphys778. Bibcode: 2007NatPh...3..861R. 
  26. ↑ Novotny, C. (2009). "Sub-Doppler laser spectroscopy on relativistic beams and tests of Lorentz invariance". Physical Review A 80 (2): 022107. doi:10.1103/PhysRevA.80.022107. Bibcode: 2009PhRvA..80b2107N. 
  27. ↑ Chou, C. W.; Hume, D. B.; Rosenband, T.; Wineland, D. J. (2010). "Optical Clocks and Relativity". Science 329 (5999): 1630–1633. doi:10.1126/science.1192720. PMID 20929843. Bibcode: 2010Sci...329.1630C. https://zenodo.org/record/1230910. 

Further reading



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Ives–Stilwell_experiment&oldid=3417413"