Physics:Michelson–Morley experiment
The Michelson–Morley experiment was an attempt to measure the relative motion of the Earth and the luminiferous aether,[A 1] a supposed medium permeating space that was thought to be the carrier of light waves. The experiment was performed between April and July 1887 by American physicists Albert A. Michelson and Edward W. Morley at what is now Case Western Reserve University in Cleveland, Ohio, and published in November of the same year.[1]
The experiment compared the speed of light in perpendicular directions in an attempt to detect the relative motion of matter through the luminiferous aether ("aether wind"). The result was negative, in that Michelson and Morley found no significant difference between the speed of light in the direction of movement through the presumed aether, and the speed at right angles. This result is generally considered to be the first strong evidence against some aether theories, as well as initiating a line of research that eventually led to special relativity, which rules out motion against an aether.[A 2] Of this experiment, Albert Einstein wrote, "If the Michelson–Morley experiment had not brought us into serious embarrassment, no one would have regarded the relativity theory as a (halfway) redemption."[A 3]:219
Michelson–Morley type experiments have been repeated many times with steadily increasing sensitivity. These include experiments from 1902 to 1905, and a series of experiments in the 1920s. More recently, in 2009, optical resonator experiments confirmed the absence of any aether wind at the 10−17 level.[2][3] Together with the Ives–Stilwell and Kennedy–Thorndike experiments, Michelson–Morley type experiments form one of the fundamental tests of special relativity.[A 4]
Detecting the aether
Physics theories of the 19th century assumed that just as surface water waves must have a supporting substance, i.e., a "medium", to move across (in this case water), and audible sound requires a medium to transmit its wave motions (such as air or water), so light must also require a medium, the "luminiferous aether", to transmit its wave motions. Because light can travel through a vacuum, it was assumed that even a vacuum must be filled with aether. Because the speed of light is so great, and because material bodies pass through the aether without obvious friction or drag, it was assumed to have a highly unusual combination of properties. Designing experiments to investigate these properties was a high priority of 19th-century physics.[A 5]:411ff
Earth orbits around the Sun at a speed of around 30 km/s (18.64 mi/s), or 108,000 km/h (67,000 mph). The Earth is in motion, so two main possibilities were considered: (1) The aether is stationary and only partially dragged by Earth (proposed by Augustin-Jean Fresnel in 1818), or (2) the aether is completely dragged by Earth and thus shares its motion at Earth's surface (proposed by Sir George Stokes, 1st Baronet in 1844).[A 6] In addition, James Clerk Maxwell (1865) recognized the electromagnetic nature of light and developed what are now called Maxwell's equations, but these equations were still interpreted as describing the motion of waves through an aether, whose state of motion was unknown. Eventually, Fresnel's idea of an (almost) stationary aether was preferred because it appeared to be confirmed by the Fizeau experiment (1851) and the aberration of star light.[A 6]
According to the stationary and the partially dragged aether hypotheses, Earth and the aether are in relative motion, implying that a so-called "aether wind" (Fig. 2) should exist. Although it would be possible, in theory, for the Earth's motion to match that of the aether at one moment in time, it was not possible for the Earth to remain at rest with respect to the aether at all times, because of the variation in both the direction and the speed of the motion. At any given point on the Earth's surface, the magnitude and direction of the wind would vary with time of day and season. By analyzing the return speed of light in different directions at various different times, it was thought to be possible to measure the motion of the Earth relative to the aether. The expected relative difference in the measured speed of light was quite small, given that the velocity of the Earth in its orbit around the Sun has a magnitude of about one hundredth of one percent of the speed of light.[A 5]:417ff
During the mid-19th century, measurements of aether wind effects of first order, i.e., effects proportional to v/c (v being Earth's velocity, c the speed of light) were thought to be possible, but no direct measurement of the speed of light was possible with the accuracy required. For instance, the Fizeau wheel could measure the speed of light to perhaps 5% accuracy, which was quite inadequate for measuring directly a first-order 0.01% change in the speed of light. A number of physicists therefore attempted to make measurements of indirect first-order effects not of the speed of light itself, but of variations in the speed of light (see First order aether-drift experiments). The Hoek experiment, for example, was intended to detect interferometric fringe shifts due to speed differences of oppositely propagating light waves through water at rest. The results of such experiments were all negative.[A 7] This could be explained by using Fresnel's dragging coefficient, according to which the aether and thus light are partially dragged by moving matter. Partial aether-dragging would thwart attempts to measure any first order change in the speed of light. As pointed out by Maxwell (1878), only experimental arrangements capable of measuring second order effects would have any hope of detecting aether drift, i.e., effects proportional to v2/c2.[A 8][A 9] Existing experimental setups, however, were not sensitive enough to measure effects of that size.
1881 and 1887 experiments
Michelson experiment (1881)

Michelson had a solution to the problem of how to construct a device sufficiently accurate to detect aether flow. In 1877, while teaching at his alma mater, the United States Naval Academy in Annapolis, Michelson conducted his first known light speed experiments as a part of a classroom demonstration. In 1881, he left active U.S. Naval service while in Germany concluding his studies. In that year, Michelson used a prototype experimental device to make several more measurements.
The device he designed, later known as a Michelson interferometer, sent yellow light from a sodium flame (for alignment), or white light (for the actual observations), through a half-silvered mirror that was used to split it into two beams traveling at right angles to one another. After leaving the splitter, the beams traveled out to the ends of long arms where they were reflected back into the middle by small mirrors. They then recombined on the far side of the splitter in an eyepiece, producing a pattern of constructive and destructive interference whose transverse displacement would depend on the relative time it takes light to transit the longitudinal vs. the transverse arms. If the Earth is traveling through an aether medium, a light beam traveling parallel to the flow of that aether will take longer to reflect back and forth than would a beam traveling perpendicular to the aether, because the increase in elapsed time from traveling against the aether wind is more than the time saved by traveling with the aether wind. Michelson expected that the Earth's motion would produce a fringe shift equal to 0.04 fringes—that is, of the separation between areas of the same intensity. He did not observe the expected shift; the greatest average deviation that he measured (in the northwest direction) was only 0.018 fringes; most of his measurements were much less. His conclusion was that Fresnel's hypothesis of a stationary aether with partial aether dragging would have to be rejected, and thus he confirmed Stokes' hypothesis of complete aether dragging.[4]
However, Alfred Potier (and later Hendrik Lorentz) pointed out to Michelson that he had made an error of calculation, and that the expected fringe shift should have been only 0.02 fringes. Michelson's apparatus was subject to experimental errors far too large to say anything conclusive about the aether wind. Definitive measurement of the aether wind would require an experiment with greater accuracy and better controls than the original. Nevertheless, the prototype was successful in demonstrating that the basic method was feasible.[A 6][A 10]
Michelson–Morley experiment (1887)
In 1885, Michelson began a collaboration with Edward Morley, spending considerable time and money to confirm with higher accuracy Fizeau's 1851 experiment on Fresnel's drag coefficient,[5] to improve on Michelson's 1881 experiment,[1] and to establish the wavelength of light as a standard of length.[6][7] At this time Michelson was professor of physics at the Case School of Applied Science, and Morley was professor of chemistry at Western Reserve University (WRU), which shared a campus with the Case School on the eastern edge of Cleveland. Michelson suffered a mental health crisis in September 1885, from which he recovered by October 1885. Morley ascribed this breakdown to the intense work of Michelson during the preparation of the experiments. In 1886, Michelson and Morley successfully confirmed Fresnel's drag coefficient – this result was also considered as a confirmation of the stationary aether concept.[A 2]
This result strengthened their hope of finding the aether wind. Michelson and Morley created an improved version of the Michelson experiment with more than enough accuracy to detect this hypothetical effect. The experiment was performed in several periods of concentrated observations between April and July 1887, in the basement of Adelbert Dormitory of WRU (later renamed Pierce Hall, demolished in 1962).[A 11][A 12]
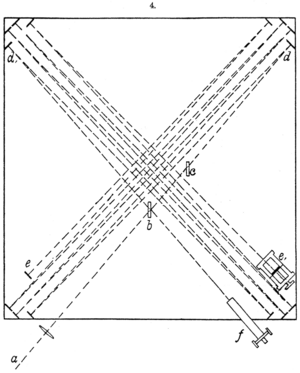
As shown in Fig. 5, the light was repeatedly reflected back and forth along the arms of the interferometer, increasing the path length to 11 m (36 ft). At this length, the drift would be about 0.4 fringes. To make that easily detectable, the apparatus was assembled in a closed room in the basement of the heavy stone dormitory, eliminating most thermal and vibrational effects. Vibrations were further reduced by building the apparatus on top of a large block of sandstone (Fig. 1), about a foot thick and five feet (1.5 m) square, which was then floated in a circular trough of mercury. They estimated that effects of about 0.01 fringe would be detectable.
Michelson and Morley and other early experimentalists using interferometric techniques in an attempt to measure the properties of the luminiferous aether, used (partially) monochromatic light only for initially setting up their equipment, always switching to white light for the actual measurements. The reason is that measurements were recorded visually. Purely monochromatic light would result in a uniform fringe pattern. Lacking modern means of environmental temperature control, experimentalists struggled with continual fringe drift even when the interferometer was set up in a basement. Because the fringes would occasionally disappear due to vibrations caused by passing horse traffic, distant thunderstorms and the like, an observer could easily "get lost" when the fringes returned to visibility. The advantages of white light, which produced a distinctive colored fringe pattern, far outweighed the difficulties of aligning the apparatus due to its low coherence length. As Dayton Miller wrote, "White light fringes were chosen for the observations because they consist of a small group of fringes having a central, sharply defined black fringe which forms a permanent zero reference mark for all readings."[A 13][note 3] Use of partially monochromatic light (yellow sodium light) during initial alignment enabled the researchers to locate the position of equal path length, more or less easily, before switching to white light.[note 4]
The mercury trough allowed the device to turn with close to zero friction, so that once having given the sandstone block a single push it would slowly rotate through the entire range of possible angles to the "aether wind", while measurements were continuously observed by looking through the eyepiece. The hypothesis of aether drift implies that because one of the arms would inevitably turn into the direction of the wind at the same time that another arm was turning perpendicularly to the wind, an effect should be noticeable even over a period of minutes.
The expectation was that the effect would be graphable as a sine wave with two peaks and two troughs per rotation of the device. This result could have been expected because during each full rotation, each arm would be parallel to the wind twice (facing into and away from the wind giving identical readings) and perpendicular to the wind twice. Additionally, due to the Earth's rotation, the wind would be expected to show periodic changes in direction and magnitude during the course of a sidereal day.
Because of the motion of the Earth around the Sun, the measured data were also expected to show annual variations.
Most famous "failed" experiment

After all this thought and preparation, the experiment became what has been called the most famous failed experiment in history.[A 1] Instead of providing insight into the properties of the aether, Michelson and Morley's article in the American Journal of Science reported the measurement to be as small as one-fortieth of the expected displacement (Fig. 7), but "since the displacement is proportional to the square of the velocity" they concluded that the measured velocity was "probably less than one-sixth" of the expected velocity of the Earth's motion in orbit and "certainly less than one-fourth".[1] Although this small "velocity" was measured, it was considered far too small to be used as evidence of speed relative to the aether, and it was understood to be within the range of an experimental error that would allow the speed to actually be zero.[A 2] For instance, Michelson wrote about the "decidedly negative result" in a letter to Lord Rayleigh in August 1887:[A 14]
The Experiments on the relative motion of the earth and ether have been completed and the result decidedly negative. The expected deviation of the interference fringes from the zero should have been 0.40 of a fringe – the maximum displacement was 0.02 and the average much less than 0.01 – and then not in the right place. As displacement is proportional to squares of the relative velocities it follows that if the ether does slip past the relative velocity is less than one sixth of the earth’s velocity.—Albert Abraham Michelson, 1887
From the standpoint of the then current aether models, the experimental results were conflicting. The Fizeau experiment and its 1886 repetition by Michelson and Morley apparently confirmed the stationary aether with partial aether dragging, and refuted complete aether dragging. On the other hand, the much more precise Michelson–Morley experiment (1887) apparently confirmed complete aether dragging and refuted the stationary aether.[A 6] In addition, the Michelson–Morley null result was further substantiated by the null results of other second-order experiments of different kind, namely the Trouton–Noble experiment (1903) and the experiments of Rayleigh and Brace (1902–1904). These problems and their solution led to the development of the Lorentz transformation and special relativity.
After the "failed" experiment Michelson and Morley ceased their aether drift measurements and started to use their newly developed technique to establish the wavelength of light as a standard of length.[6][7]
Light path analysis and consequences
Observer resting in the aether
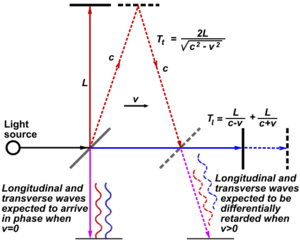
The beam travel time in the longitudinal direction can be derived as follows:[A 15] Light is sent from the source and propagates with the speed of light [math]\displaystyle{ c }[/math] in the aether. It passes through the half-silvered mirror at the origin at [math]\displaystyle{ T=0 }[/math]. The reflecting mirror is at that moment at distance [math]\displaystyle{ L }[/math] (the length of the interferometer arm) and is moving with velocity [math]\displaystyle{ v }[/math]. The beam hits the mirror at time [math]\displaystyle{ T_1 }[/math] and thus travels the distance [math]\displaystyle{ cT_1 }[/math]. At this time, the mirror has traveled the distance [math]\displaystyle{ vT_1 }[/math]. Thus [math]\displaystyle{ cT_1 =L+vT_1 }[/math] and consequently the travel time [math]\displaystyle{ T_1=L/(c-v) }[/math]. The same consideration applies to the backward journey, with the sign of [math]\displaystyle{ v }[/math] reversed, resulting in [math]\displaystyle{ cT_2 =L-vT_2 }[/math] and [math]\displaystyle{ T_2 =L/(c+v) }[/math]. The total travel time [math]\displaystyle{ T_\ell=T_1+T_2 }[/math] is:
- [math]\displaystyle{ T_\ell=\frac{L}{c-v}+\frac{L}{c+v} =\frac{2L}{c}\frac{1}{1-\frac{v^2}{c^2}} \approx\frac{2L}{c} \left(1+\frac{v^2}{c^2}\right) }[/math]
Michelson obtained this expression correctly in 1881, however, in transverse direction he obtained the incorrect expression
- [math]\displaystyle{ T_t=\frac{2L}{c}, }[/math]
because he overlooked the increase in path length in the rest frame of the aether. This was corrected by Alfred Potier (1882) and Hendrik Lorentz (1886). The derivation in the transverse direction can be given as follows (analogous to the derivation of time dilation using a light clock): The beam is propagating at the speed of light [math]\displaystyle{ c }[/math] and hits the mirror at time [math]\displaystyle{ T_3 }[/math], traveling the distance [math]\displaystyle{ cT_3 }[/math]. At the same time, the mirror has traveled the distance [math]\displaystyle{ vT_3 }[/math] in the x direction. So in order to hit the mirror, the travel path of the beam is [math]\displaystyle{ L }[/math] in the y direction (assuming equal-length arms) and [math]\displaystyle{ vT_3 }[/math] in the x direction. This inclined travel path follows from the transformation from the interferometer rest frame to the aether rest frame. Therefore, the Pythagorean theorem gives the actual beam travel distance of [math]\displaystyle{ \sqrt{L^2+\left(vT_3\right)^2} }[/math]. Thus [math]\displaystyle{ cT_3 =\sqrt{L^2+\left(vT_3\right)^2} }[/math] and consequently the travel time [math]\displaystyle{ T_3 =L/\sqrt{c^2-v^2} }[/math], which is the same for the backward journey. The total travel time [math]\displaystyle{ T_t=2T_3 }[/math] is:
- [math]\displaystyle{ T_t=\frac{2L}{\sqrt{c^2-v^2}}=\frac{2L}{c}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\approx\frac{2L}{c} \left(1+\frac{v^2}{2c^2}\right) }[/math]
The time difference between [math]\displaystyle{ T_\ell }[/math] and [math]\displaystyle{ T_t }[/math] is given by[A 16]
- [math]\displaystyle{ T_\ell-T_t=\frac{2L}{c}\left(\frac{1}{1-\frac{v^2}{c^2}}-\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\right) }[/math]
To find the path difference, simply multiply by [math]\displaystyle{ c }[/math];
[math]\displaystyle{ \Delta{\lambda}_1=2L\left(\frac{1}{1-\frac{v^2}{c^2}}-\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\right) }[/math]
The path difference is denoted by [math]\displaystyle{ \Delta \lambda }[/math] because the beams are out of phase by a some number of wavelengths ([math]\displaystyle{ \lambda }[/math]). To visualise this, consider taking the two beam paths along the longitudinal and transverse plane, and lying them straight (an animation of this is shown at minute 11:00, The Mechanical Universe, episode 41[8]). One path will be longer than the other, this distance is [math]\displaystyle{ \Delta \lambda }[/math]. Alternatively, consider the rearrangement of the speed of light formula [math]\displaystyle{ c{\Delta}T = \Delta\lambda }[/math] .
If the relation [math]\displaystyle{ {v^2}/{c^2} \lt \lt 1 }[/math] is true (if the velocity of the aether is small relative to the speed of light), then the expression can be simplified using a first order binomial expansion;
[math]\displaystyle{ (1-x)^n \approx {1-nx} }[/math]
So, rewriting the above in terms of powers;
[math]\displaystyle{ \Delta{\lambda}_1 = 2L\left(\left({1-\frac{v^2}{c^2}}\right)^{-1}-\left(1-\frac{v^2}{c^2}\right)^{-1/2}\right) }[/math]
Applying binomial simplification;[9]
[math]\displaystyle{ \Delta{\lambda}_1 = 2L\left( (1+\frac{v^2}{c^2}) - (1+\frac{v^2}{2c^2})\right)={2L}\frac{v^2}{2c^2} }[/math]
Therefore;
[math]\displaystyle{ \Delta{\lambda}_1={L}\frac{v^2}{c^2} }[/math]
It can be seen from this derivation that aether wind manifests as a path difference. The path difference is zero only when the interferometer is aligned with or perpendicular to the aether wind, and it reaches a maximum when it is at a 45° angle. The path difference can be any fraction of the wavelength, depending on the angle and speed of the aether wind.
To prove the existence of the aether, Michaelson and Morley sought to find the "fringe shift". The idea was simple, the fringes of the interference pattern should shift when rotating it by 90° as the two beams have exchanged roles. To find the fringe shift, subtract the path difference in first orientation by the path difference in the second, then divide by the wavelength, [math]\displaystyle{ \lambda }[/math], of light;[9]
- [math]\displaystyle{ n=\frac{\Delta\lambda_1-\Delta\lambda_2}{\lambda}\approx\frac{2Lv^2}{\lambda c^2}. }[/math]
Note the difference between [math]\displaystyle{ \Delta \lambda }[/math], which is some number of wavelengths, and [math]\displaystyle{ \lambda }[/math] which is a single wavelength. As can be seen by this relation, fringe shift n is a unitless quantity.
Since L ≈ 11 meters and λ ≈ 500 nanometers, the expected fringe shift was n ≈ 0.44. The negative result led Michelson to the conclusion that there is no measurable aether drift.[1] However, he never accepted this on a personal level, and the negative result haunted him for the rest of his life (Source; The Mechanical Universe, episode 41[8]).
Observer comoving with the interferometer
If the same situation is described from the view of an observer co-moving with the interferometer, then the effect of aether wind is similar to the effect experienced by a swimmer, who tries to move with velocity [math]\displaystyle{ c }[/math] against a river flowing with velocity [math]\displaystyle{ v }[/math].[A 17]
In the longitudinal direction the swimmer first moves upstream, so his velocity is diminished due to the river flow to [math]\displaystyle{ c-v }[/math]. On his way back moving downstream, his velocity is increased to [math]\displaystyle{ c+v }[/math]. This gives the beam travel times [math]\displaystyle{ T_1 }[/math] and [math]\displaystyle{ T_2 }[/math] as mentioned above.
In the transverse direction, the swimmer has to compensate for the river flow by moving at a certain angle against the flow direction, in order to sustain his exact transverse direction of motion and to reach the other side of the river at the correct location. This diminishes his speed to [math]\displaystyle{ \sqrt{c^2-v^2} }[/math], and gives the beam travel time [math]\displaystyle{ T_3 }[/math] as mentioned above.
Mirror reflection
The classical analysis predicted a relative phase shift between the longitudinal and transverse beams which in Michelson and Morley's apparatus should have been readily measurable. What is not often appreciated (since there was no means of measuring it), is that motion through the hypothetical aether should also have caused the two beams to diverge as they emerged from the interferometer by about 10−8 radians.[A 18]
For an apparatus in motion, the classical analysis requires that the beam-splitting mirror be slightly offset from an exact 45° if the longitudinal and transverse beams are to emerge from the apparatus exactly superimposed. In the relativistic analysis, Lorentz-contraction of the beam splitter in the direction of motion causes it to become more perpendicular by precisely the amount necessary to compensate for the angle discrepancy of the two beams.[A 18]
Length contraction and Lorentz transformation
A first step to explaining the Michelson and Morley experiment's null result was found in the FitzGerald–Lorentz contraction hypothesis, now simply called length contraction or Lorentz contraction, first proposed by George FitzGerald (1889) in a letter to same journal that published the Michelson-Morley paper, as "almost the only hypothesis that can reconcile" the apparent contradictions. It was independently also proposed by Hendrik Lorentz (1892).[A 19] According to this law all objects physically contract by [math]\displaystyle{ L/\gamma }[/math] along the line of motion (originally thought to be relative to the aether), [math]\displaystyle{ \gamma=1/\sqrt{1-v^2/c^2} }[/math] being the Lorentz factor. This hypothesis was partly motivated by Oliver Heaviside's discovery in 1888 that electrostatic fields are contracting in the line of motion. But since there was no reason at that time to assume that binding forces in matter are of electric origin, length contraction of matter in motion with respect to the aether was considered an ad hoc hypothesis.[A 10]
If length contraction of [math]\displaystyle{ L }[/math] is inserted into the above formula for [math]\displaystyle{ T_\ell }[/math], then the light propagation time in the longitudinal direction becomes equal to that in the transverse direction:
- [math]\displaystyle{ T_\ell=\frac{2L\sqrt{1-\frac{v^2}{c^2}}}{c}\frac{1}{1-\frac{v^2}{c^2}}=\frac{2L}{c} \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}=T_t }[/math]
However, length contraction is only a special case of the more general relation, according to which the transverse length is larger than the longitudinal length by the ratio [math]\displaystyle{ \gamma }[/math]. This can be achieved in many ways. If [math]\displaystyle{ L_1 }[/math] is the moving longitudinal length and [math]\displaystyle{ L_2 }[/math] the moving transverse length, [math]\displaystyle{ L'_1=L'_2 }[/math] being the rest lengths, then it is given:[A 20]
- [math]\displaystyle{ \frac{L_2}{L_1}=\frac{L'_2}{\varphi}\left/\frac{L'_1}{\gamma\varphi}\right.=\gamma. }[/math]
[math]\displaystyle{ \varphi }[/math] can be arbitrarily chosen, so there are infinitely many combinations to explain the Michelson–Morley null result. For instance, if [math]\displaystyle{ \varphi=1 }[/math] the relativistic value of length contraction of [math]\displaystyle{ L_1 }[/math] occurs, but if [math]\displaystyle{ \varphi=1/\gamma }[/math] then no length contraction but an elongation of [math]\displaystyle{ L_2 }[/math] occurs. This hypothesis was later extended by Joseph Larmor (1897), Lorentz (1904) and Henri Poincaré (1905), who developed the complete Lorentz transformation including time dilation in order to explain the Trouton–Noble experiment, the Experiments of Rayleigh and Brace, and Kaufmann's experiments. It has the form
- [math]\displaystyle{ x'=\gamma\varphi(x-vt),\ y'=\varphi y,\ z'=\varphi z,\ t'=\gamma\varphi\left(t-\frac{vx}{c^2}\right) }[/math]
It remained to define the value of [math]\displaystyle{ \varphi }[/math], which was shown by Lorentz (1904) to be unity.[A 20] In general, Poincaré (1905)[A 21] demonstrated that only [math]\displaystyle{ \varphi=1 }[/math] allows this transformation to form a group, so it is the only choice compatible with the principle of relativity, i.e., making the stationary aether undetectable. Given this, length contraction and time dilation obtain their exact relativistic values.
Special relativity
Albert Einstein formulated the theory of special relativity by 1905, deriving the Lorentz transformation and thus length contraction and time dilation from the relativity postulate and the constancy of the speed of light, thus removing the ad hoc character from the contraction hypothesis. Einstein emphasized the kinematic foundation of the theory and the modification of the notion of space and time, with the stationary aether no longer playing any role in his theory. He also pointed out the group character of the transformation. Einstein was motivated by Maxwell's theory of electromagnetism (in the form as it was given by Lorentz in 1895) and the lack of evidence for the luminiferous aether.[A 22]
This allows a more elegant and intuitive explanation of the Michelson–Morley null result. In a comoving frame the null result is self-evident, since the apparatus can be considered as at rest in accordance with the relativity principle, thus the beam travel times are the same. In a frame relative to which the apparatus is moving, the same reasoning applies as described above in "Length contraction and Lorentz transformation", except the word "aether" has to be replaced by "non-comoving inertial frame". Einstein wrote in 1916:[A 23]
Although the estimated difference between these two times is exceedingly small, Michelson and Morley performed an experiment involving interference in which this difference should have been clearly detectable. But the experiment gave a negative result — a fact very perplexing to physicists. Lorentz and FitzGerald rescued the theory from this difficulty by assuming that the motion of the body relative to the æther produces a contraction of the body in the direction of motion, the amount of contraction being just sufficient to compensate for the difference in time mentioned above. Comparison with the discussion in Section 11 shows that also from the standpoint of the theory of relativity this solution of the difficulty was the right one. But on the basis of the theory of relativity the method of interpretation is incomparably more satisfactory. According to this theory there is no such thing as a "specially favoured" (unique) co-ordinate system to occasion the introduction of the æther-idea, and hence there can be no æther-drift, nor any experiment with which to demonstrate it. Here the contraction of moving bodies follows from the two fundamental principles of the theory, without the introduction of particular hypotheses; and as the prime factor involved in this contraction we find, not the motion in itself, to which we cannot attach any meaning, but the motion with respect to the body of reference chosen in the particular case in point. Thus for a co-ordinate system moving with the earth the mirror system of Michelson and Morley is not shortened, but it is shortened for a co-ordinate system which is at rest relatively to the sun.—Albert Einstein, 1916
The extent to which the null result of the Michelson–Morley experiment influenced Einstein is disputed. Alluding to some statements of Einstein, many historians argue that it played no significant role in his path to special relativity,[A 24][A 25] while other statements of Einstein probably suggest that he was influenced by it.[A 26] In any case, the null result of the Michelson–Morley experiment helped the notion of the constancy of the speed of light gain widespread and rapid acceptance.[A 24]
It was later shown by Howard Percy Robertson (1949) and others[A 4][A 27] (see Robertson–Mansouri–Sexl test theory), that it is possible to derive the Lorentz transformation entirely from the combination of three experiments. First, the Michelson–Morley experiment showed that the speed of light is independent of the orientation of the apparatus, establishing the relationship between longitudinal (β) and transverse (δ) lengths. Then in 1932, Roy Kennedy and Edward Thorndike modified the Michelson–Morley experiment by making the path lengths of the split beam unequal, with one arm being very short.[10] The Kennedy–Thorndike experiment took place for many months as the Earth moved around the sun. Their negative result showed that the speed of light is independent of the velocity of the apparatus in different inertial frames. In addition it established that besides length changes, corresponding time changes must also occur, i.e., it established the relationship between longitudinal lengths (β) and time changes (α). So both experiments do not provide the individual values of these quantities. This uncertainty corresponds to the undefined factor [math]\displaystyle{ \varphi }[/math] as described above. It was clear due to theoretical reasons (the group character of the Lorentz transformation as required by the relativity principle) that the individual values of length contraction and time dilation must assume their exact relativistic form. But a direct measurement of one of these quantities was still desirable to confirm the theoretical results. This was achieved by the Ives–Stilwell experiment (1938), measuring α in accordance with time dilation. Combining this value for α with the Kennedy–Thorndike null result shows that β must assume the value of relativistic length contraction. Combining β with the Michelson–Morley null result shows that δ must be zero. Therefore, the Lorentz transformation with [math]\displaystyle{ \varphi=1 }[/math] is an unavoidable consequence of the combination of these three experiments.[A 4]
Special relativity is generally considered the solution to all negative aether drift (or isotropy of the speed of light) measurements, including the Michelson–Morley null result. Many high precision measurements have been conducted as tests of special relativity and modern searches for Lorentz violation in the photon, electron, nucleon, or neutrino sector, all of them confirming relativity.
Incorrect alternatives
As mentioned above, Michelson initially believed that his experiment would confirm Stokes' theory, according to which the aether was fully dragged in the vicinity of the earth (see Aether drag hypothesis). However, complete aether drag contradicts the observed aberration of light and was contradicted by other experiments as well. In addition, Lorentz showed in 1886 that Stokes's attempt to explain aberration is contradictory.[A 6][A 5]
Furthermore, the assumption that the aether is not carried in the vicinity, but only within matter, was very problematic as shown by the Hammar experiment (1935). Hammar directed one leg of his interferometer through a heavy metal pipe plugged with lead. If aether were dragged by mass, it was theorized that the mass of the sealed metal pipe would have been enough to cause a visible effect. Once again, no effect was seen, so aether-drag theories are considered to be disproven.
Walther Ritz's emission theory (or ballistic theory) was also consistent with the results of the experiment, not requiring aether. The theory postulates that light has always the same velocity in respect to the source.[A 28] However de Sitter noted that emitter theory predicted several optical effects that were not seen in observations of binary stars in which the light from the two stars could be measured in a spectrometer. If emission theory were correct, the light from the stars should experience unusual fringe shifting due to the velocity of the stars being added to the speed of the light, but no such effect could be seen. It was later shown by J. G. Fox that the original de Sitter experiments were flawed due to extinction,[11] but in 1977 Brecher observed X-rays from binary star systems with similar null results.[12] Furthermore, Filippas and Fox (1964) conducted terrestrial particle accelerator tests specifically designed to address Fox's earlier "extinction" objection, the results being inconsistent with source dependence of the speed of light.[13]
Subsequent experiments
Although Michelson and Morley went on to different experiments after their first publication in 1887, both remained active in the field. Other versions of the experiment were carried out with increasing sophistication.[A 29][A 30] Morley was not convinced of his own results, and went on to conduct additional experiments with Dayton Miller from 1902 to 1904. Again, the result was negative within the margins of error.[14][15]
Miller worked on increasingly larger interferometers, culminating in one with a 32-meter (105 ft) (effective) arm length that he tried at various sites, including on top of a mountain at the Mount Wilson Observatory. To avoid the possibility of the aether wind being blocked by solid walls, his mountaintop observations used a special shed with thin walls, mainly of canvas. From noisy, irregular data, he consistently extracted a small positive signal that varied with each rotation of the device, with the sidereal day, and on a yearly basis. His measurements in the 1920s amounted to approximately 10 km/s (6.2 mi/s) instead of the nearly 30 km/s (18.6 mi/s) expected from the Earth's orbital motion alone. He remained convinced this was due to partial entrainment or aether dragging, though he did not attempt a detailed explanation. He ignored critiques demonstrating the inconsistency of his results and the refutation by the Hammar experiment.[A 31][note 5] Miller's findings were considered important at the time, and were discussed by Michelson, Lorentz and others at a meeting reported in 1928.[A 32] There was general agreement that more experimentation was needed to check Miller's results. Miller later built a non-magnetic device to eliminate magnetostriction, while Michelson built one of non-expanding Invar to eliminate any remaining thermal effects. Other experimenters from around the world increased accuracy, eliminated possible side effects, or both. So far, no one has been able to replicate Miller's results, and modern experimental accuracies have ruled them out.[A 33] Roberts (2006) has pointed out that the primitive data reduction techniques used by Miller and other early experimenters, including Michelson and Morley, were capable of creating apparent periodic signals even when none existed in the actual data. After reanalyzing Miller's original data using modern techniques of quantitative error analysis, Roberts found Miller's apparent signals to be statistically insignificant.[A 34]
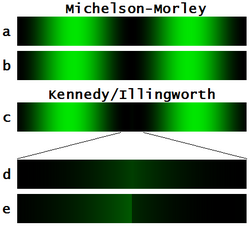
Using a special optical arrangement involving a 1/20 wave step in one mirror, Roy J. Kennedy (1926) and K.K. Illingworth (1927) (Fig. 8) converted the task of detecting fringe shifts from the relatively insensitive one of estimating their lateral displacements to the considerably more sensitive task of adjusting the light intensity on both sides of a sharp boundary for equal luminance.[16][17] If they observed unequal illumination on either side of the step, such as in Fig. 8e, they would add or remove calibrated weights from the interferometer until both sides of the step were once again evenly illuminated, as in Fig. 8d. The number of weights added or removed provided a measure of the fringe shift. Different observers could detect changes as little as 1/1500 to 1/300 of a fringe. Kennedy also carried out an experiment at Mount Wilson, finding only about 1/10 the drift measured by Miller and no seasonal effects.[A 32]
In 1930, Georg Joos conducted an experiment using an automated interferometer with 21-meter-long (69 ft) arms forged from pressed quartz having a very low coefficient of thermal expansion, that took continuous photographic strip recordings of the fringes through dozens of revolutions of the apparatus. Displacements of 1/1000 of a fringe could be measured on the photographic plates. No periodic fringe displacements were found, placing an upper limit to the aether wind of 1.5 km/s (0.93 mi/s).[18]
In the table below, the expected values are related to the relative speed between Earth and Sun of 30 km/s (18.6 mi/s). With respect to the speed of the solar system around the galactic center of about 220 km/s (140 mi/s), or the speed of the solar system relative to the CMB rest frame of about 370 km/s (230 mi/s), the null results of those experiments are even more obvious.
| Name | Location | Year | Arm length (meters) | Fringe shift expected | Fringe shift measured | Ratio | Upper Limit on Vaether | Experimental Resolution | Null result |
|---|---|---|---|---|---|---|---|---|---|
| Michelson[4] | Potsdam | 1881 | 1.2 | 0.04 | ≤ 0.02 | 2 | ~ 20 km/s | 0.02 | [math]\displaystyle{ \approx }[/math] yes |
| Michelson and Morley[1] | Cleveland | 1887 | 11.0 | 0.4 | < 0.02 or ≤ 0.01 |
40 | ~ 4–8 km/s | 0.01 | [math]\displaystyle{ \approx }[/math] yes |
| Morley and Miller[14][15] | Cleveland | 1902–1904 | 32.2 | 1.13 | ≤ 0.015 | 80 | ~ 3.5 km/s | 0.015 | yes |
| Miller[19] | Mt. Wilson | 1921 | 32.0 | 1.12 | ≤ 0.08 | 15 | ~ 8–10 km/s | unclear | unclear |
| Miller[19] | Cleveland | 1923–1924 | 32.0 | 1.12 | ≤ 0.03 | 40 | ~ 5 km/s | 0.03 | yes |
| Miller (sunlight)[19] | Cleveland | 1924 | 32.0 | 1.12 | ≤ 0.014 | 80 | ~ 3 km/s | 0.014 | yes |
| Tomaschek (star light)[20] | Heidelberg | 1924 | 8.6 | 0.3 | ≤ 0.02 | 15 | ~ 7 km/s | 0.02 | yes |
| Miller[19][A 13] | Mt. Wilson | 1925–1926 | 32.0 | 1.12 | ≤ 0.088 | 13 | ~ 8–10 km/s | unclear | unclear |
| Kennedy[16] | Pasadena/Mt. Wilson | 1926 | 2.0 | 0.07 | ≤ 0.002 | 35 | ~ 5 km/s | 0.002 | yes |
| Illingworth[17] | Pasadena | 1927 | 2.0 | 0.07 | ≤ 0.0004 | 175 | ~ 2 km/s | 0.0004 | yes |
| Piccard & Stahel[21] | with a Balloon | 1926 | 2.8 | 0.13 | ≤ 0.006 | 20 | ~ 7 km/s | 0.006 | yes |
| Piccard & Stahel[22] | Brussels | 1927 | 2.8 | 0.13 | ≤ 0.0002 | 185 | ~ 2.5 km/s | 0.0007 | yes |
| Piccard & Stahel[23] | Rigi | 1927 | 2.8 | 0.13 | ≤ 0.0003 | 185 | ~ 2.5 km/s | 0.0007 | yes |
| Michelson et al.[24] | Pasadena (Mt. Wilson optical shop) | 1929 | 25.9 | 0.9 | ≤ 0.01 | 90 | ~ 3 km/s | 0.01 | yes |
| Joos[18] | Jena | 1930 | 21.0 | 0.75 | ≤ 0.002 | 375 | ~ 1.5 km/s | 0.002 | yes |
Recent experiments
Optical tests
Optical tests of the isotropy of the speed of light became commonplace.[A 35] New technologies, including the use of lasers and masers, have significantly improved measurement precision. (In the following table, only Essen (1955), Jaseja (1964), and Shamir/Fox (1969) are experiments of Michelson–Morley type, i.e., comparing two perpendicular beams. The other optical experiments employed different methods.)
| Author | Year | Description | Upper bounds |
|---|---|---|---|
| Louis Essen[25] | 1955 | The frequency of a rotating microwave cavity resonator is compared with that of a quartz clock | ~3 km/s |
| Cedarholm et al.[26][27] | 1958 | Two ammonia masers were mounted on a rotating table, and their beams were directed in opposite directions. | ~30 m/s |
| Mössbauer rotor experiments | 1960–68 | In a series of experiments by different researchers, the frequencies of gamma rays were observed using the Mössbauer effect. | ~2.0 cm/s |
| Jaseja et al.[28] | 1964 | The frequencies of two He–Ne masers, mounted on a rotating table, were compared. Unlike Cedarholm et al., the masers were placed perpendicular to each other. | ~30 m/s |
| Shamir and Fox[29] | 1969 | Both arms of the interferometer were contained in a transparent solid (plexiglass). The light source was a Helium–neon laser. | ~7 km/s |
| Trimmer et al.[30][31] | 1973 | They searched for anisotropies of the speed of light behaving as the first and third of the Legendre polynomials. They used a triangle interferometer, with one portion of the path in glass. (In comparison, the Michelson–Morley type experiments test the second Legendre polynomial)[A 27] | ~2.5 cm/s |
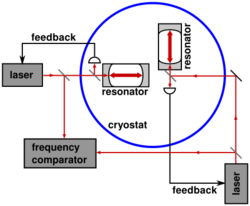
Recent optical resonator experiments
During the early 21st century, there has been a resurgence in interest in performing precise Michelson–Morley type experiments using lasers, masers, cryogenic optical resonators, etc. This is in large part due to predictions of quantum gravity that suggest that special relativity may be violated at scales accessible to experimental study. The first of these highly accurate experiments was conducted by Brillet & Hall (1979), in which they analyzed a laser frequency stabilized to a resonance of a rotating optical Fabry–Pérot cavity. They set a limit on the anisotropy of the speed of light resulting from the Earth's motions of Δc/c ≈ 10−15, where Δc is the difference between the speed of light in the x- and y-directions.[33]
As of 2015, optical and microwave resonator experiments have improved this limit to Δc/c ≈ 10−18. In some of them, the devices were rotated or remained stationary, and some were combined with the Kennedy–Thorndike experiment. In particular, Earth's direction and velocity (ca. 368 km/s (229 mi/s)) relative to the CMB rest frame are ordinarily used as references in these searches for anisotropies.
| Author | Year | Description | Δc/c |
|---|---|---|---|
| Wolf et al.[34] | 2003 | The frequency of a stationary cryogenic microwave oscillator, consisting of sapphire crystal operating in a whispering gallery mode, is compared to a hydrogen maser whose frequency was compared to caesium and rubidium atomic fountain clocks. Changes during Earth's rotation have been searched for. Data between 2001 and 2002 was analyzed. | [math]\displaystyle{ \lesssim10^{-15} }[/math] |
| Müller et al.[32] | 2003 | Two optical resonators constructed from crystalline sapphire, controlling the frequencies of two Nds, are set at right angles within a helium cryostat. A frequency comparator measures the beat frequency of the combined outputs of the two resonators. | |
| Wolf et al.[35] | 2004 | See Wolf et al. (2003). An active temperature control was implemented. Data between 2002 and 2003 was analyzed. | |
| Wolf et al.[36] | 2004 | See Wolf et al. (2003). Data between 2002 and 2004 was analyzed. | |
| Antonini et al.[37] | 2005 | Similar to Müller et al. (2003), though the apparatus itself was set into rotation. Data between 2002 and 2004 was analyzed. | [math]\displaystyle{ \lesssim10^{-16} }[/math] |
| Stanwix et al.[38] | 2005 | Similar to Wolf et al. (2003). The frequency of two cryogenic oscillators was compared. In addition, the apparatus was set into rotation. Data between 2004 and 2005 was analyzed. | |
| Herrmann et al.[39] | 2005 | Similar to Müller et al. (2003). The frequencies of two optical Fabry–Pérot resonators cavities are compared – one cavity was continuously rotating while the other one was stationary oriented north–south. Data between 2004 and 2005 was analyzed. | |
| Stanwix et al.[40] | 2006 | See Stanwix et al. (2005). Data between 2004 and 2006 was analyzed. | |
| Müller et al.[41] | 2007 | See Herrmann et al. (2005) and Stanwix et al. (2006). Data of both groups collected between 2004 and 2006 are combined and further analyzed. Since the experiments are located at difference continents, at Berlin and Perth respectively, the effects of both the rotation of the devices themselves and the rotation of Earth could be studied. | |
| Eisele et al.[2] | 2009 | The frequencies of a pair of orthogonal oriented optical standing wave cavities are compared. The cavities were interrogated by a Nd. Data between 2007 and 2008 was analyzed. | [math]\displaystyle{ \lesssim10^{-17} }[/math] |
| Herrmann et al.[3] | 2009 | The frequencies of a pair of rotating, orthogonal optical Fabry–Pérot resonators are compared. The frequencies of two Nds are stabilized to resonances of these resonators. | |
| Nagel et al.[42] | 2015 | The frequencies of a pair of rotating, orthogonal microwave resonators are compared. |
Other tests of Lorentz invariance
Examples of other experiments not based on the Michelson–Morley principle, i.e., non-optical isotropy tests achieving an even higher level of precision, are Clock comparison or Hughes–Drever experiments. In Drever's 1961 experiment, 7Li nuclei in the ground state, which has total angular momentum J = 3/2, were split into four equally spaced levels by a magnetic field. Each transition between a pair of adjacent levels should emit a photon of equal frequency, resulting in a single, sharp spectral line. However, since the nuclear wave functions for different MJ have different orientations in space relative to the magnetic field, any orientation dependence, whether from an aether wind or from a dependence on the large-scale distribution of mass in space (see Mach's principle), would perturb the energy spacings between the four levels, resulting in an anomalous broadening or splitting of the line. No such broadening was observed. Modern repeats of this kind of experiment have provided some of the most accurate confirmations of the principle of Lorentz invariance.[A 36]
See also
- Michelson–Morley Award
- Moving magnet and conductor problem
- The Light (Glass)
- LIGO
References
Notes
- ↑ Among other lessons was the need to control for vibration. Michelson (1881) wrote: "... owing to the extreme sensitiveness of the instrument to vibrations, the work could not be carried on during the day. Next, the experiment was tried at night. When the mirrors were placed half-way on the arms the fringes were visible, but their position could not be measured till after twelve o'clock, and then only at intervals. When the mirrors were moved out to the ends of the arms, the fringes were only occasionally visible. It thus appeared that the experiments could not be performed in Berlin, and the apparatus was accordingly removed to the Astrophysicalisches Observatorium in Potsdam ... Here, the fringes under ordinary circumstances were sufficiently quiet to measure, but so extraordinarily sensitive was the instrument that the stamping of the pavement, about 100 meters from the observatory, made the fringes disappear entirely!"
- ↑ Michelson (1881) wrote: "... a sodium flame placed at a produced at once the interference bands. These could then be altered in width, position, or direction, by a slight movement of the plate b, and when they were of convenient width and of maximum sharpness, the sodium flame was removed and the lamp again substituted. The screw m was then slowly turned till the bands reappeared. They were then of course colored, except the central band, which was nearly black."
- ↑ If one uses a half-silvered mirror as the beam splitter, the reflected beam will undergo a different number of front-surface reflections than the transmitted beam. At each front-surface reflection, the light will undergo a phase inversion. Because the two beams undergo a different number of phase inversions, when the path lengths of the two beams match or differ by an integral number of wavelengths (e.g. 0, 1, 2 ...), there will be destructive interference and a weak signal at the detector. If the path lengths of the beams differ by a half-integral number of wavelengths (e.g., 0.5, 1.5, 2.5 ...), constructive interference will yield a strong signal. The results are opposite if a cube beam-splitter is used, because a cube beam-splitter makes no distinction between a front- and rear-surface reflection.
- ↑ Sodium light produces a fringe pattern that displays cycles of fuzziness and sharpness that repeat every several hundred fringes over a distance of approximately a millimeter. This pattern is due to the yellow sodium D line being actually a doublet, the individual lines of which have a limited coherence length. After aligning the interferometer to display the centermost portion of the sharpest set of fringes, the researcher would switch to white light.
- ↑ Thirring (1926) as well as Lorentz pointed out that Miller's results failed even the most basic criteria required to believe in their celestial origin, namely that the azimuth of supposed drift should exhibit daily variations consistent with the source rotating about the celestial pole. Instead, while Miller's observations showed daily variations, their oscillations in one set of experiments might center, say, around a northwest–southeast line.
Experiments
- ↑ 1.0 1.1 1.2 1.3 1.4 Michelson, Albert A.; Morley, Edward W. (1887). "On the Relative Motion of the Earth and the Luminiferous Ether". American Journal of Science 34 (203): 333–345. doi:10.2475/ajs.s3-34.203.333. Bibcode: 1887AmJS...34..333M.
- ↑ 2.0 2.1 Eisele, Ch.; Nevsky, A. Yu.; Schillerv, S. (2009). "Laboratory Test of the Isotropy of Light Propagation at the 10−17 level". Physical Review Letters 103 (9): 090401. doi:10.1103/PhysRevLett.103.090401. PMID 19792767. Bibcode: 2009PhRvL.103i0401E. http://www.exphy.uni-duesseldorf.de/Publikationen/2009/Eisele%20et%20al%20Laboratory%20Test%20of%20the%20Isotropy%20of%20Light%20Propagation%20at%20the%2010-17%20Level%202009.pdf.
- ↑ 3.0 3.1 Herrmann, S.; Senger, A.; Möhle, K.; Nagel, M.; Kovalchuk, E. V.; Peters, A. (2009). "Rotating optical cavity experiment testing Lorentz invariance at the 10−17 level". Physical Review D 80 (100): 105011. doi:10.1103/PhysRevD.80.105011. Bibcode: 2009PhRvD..80j5011H.
- ↑ 4.0 4.1 4.2 Michelson, Albert A. (1881). "The Relative Motion of the Earth and the Luminiferous Ether". American Journal of Science 22 (128): 120–129. doi:10.2475/ajs.s3-22.128.120. Bibcode: 1881AmJS...22..120M. https://zenodo.org/record/1450060.
- ↑ Michelson, Albert A.; Morley, Edward W. (1886). "Influence of Motion of the Medium on the Velocity of Light". Am. J. Sci. 31 (185): 377–386. doi:10.2475/ajs.s3-31.185.377. Bibcode: 1886AmJS...31..377M.
- ↑ 6.0 6.1 Michelson, Albert A.; Morley, Edward W. (1887). "On a method of making the wave-length of sodium light the actual and practical standard of length". American Journal of Science 34 (204): 427–430. doi:10.2475/ajs.s3-34.204.427. Bibcode: 1887AmJS...34..427M. http://www.ajsonline.org/content/s3-34/204/427.full.pdf+html.
- ↑ 7.0 7.1 Michelson, Albert A.; Morley, Edward W. (1889). "On the feasibility of establishing a light-wave as the ultimate standard of length". American Journal of Science 38 (225): 181–6. doi:10.2475/ajs.s3-38.225.181. http://www.ajsonline.org/content/s3-38/225/181.full.pdf+html.
- ↑ 8.0 8.1 "The Mechanical Universe, Episode 41". https://www.youtube.com/watch?v=Ip_jdcA8fcw&t=632s.
- ↑ 9.0 9.1 Serway, Raymond; Jewett, John (2007). Physics for Scientists and Engineers, Volume 2 (7th illustrated ed.). Cengage Learning. p. 1117. ISBN 978-0-495-11244-0. https://books.google.com/books?id=-g_y6CMkZ0IC. Extract of page 1117
- ↑ Kennedy, R. J.; Thorndike, E. M. (1932). "Experimental Establishment of the Relativity of Time". Phys. Rev. 42 (3): 400–408. doi:10.1103/PhysRev.42.400. Bibcode: 1932PhRv...42..400K.
- ↑ Fox, J. G. (1965), "Evidence Against Emission Theories", American Journal of Physics 33 (1): 1–17, doi:10.1119/1.1971219, Bibcode: 1965AmJPh..33....1F.
- ↑ Brecher, K. (1977). "Is the speed of light independent of the velocity of the source". Physical Review Letters 39 (17): 1051–1054. doi:10.1103/PhysRevLett.39.1051. Bibcode: 1977PhRvL..39.1051B.
- ↑ Filippas, T.A.; Fox, J.G. (1964). "Velocity of Gamma Rays from a Moving Source". Physical Review 135 (4B): B1071–1075. doi:10.1103/PhysRev.135.B1071. Bibcode: 1964PhRv..135.1071F.
- ↑ 14.0 14.1 Morley, Edward W.; Miller, Dayton C. (1904). "Extract from a Letter dated Cleveland, Ohio, August 5th, 1904, to Lord Kelvin from Profs. Edward W. Morley and Dayton C. Miller". Philosophical Magazine. 6 8 (48): 753–754. doi:10.1080/14786440409463248.
- ↑ 15.0 15.1 Morley, Edward W.; Miller, Dayton C. (1905). "Report of an experiment to detect the Fitzgerald–Lorentz Effect". Proceedings of the American Academy of Arts and Sciences XLI (12): 321–8. doi:10.2307/20022071.
- ↑ 16.0 16.1 Kennedy, Roy J. (1926). "A Refinement of the Michelson–Morley Experiment". Proceedings of the National Academy of Sciences 12 (11): 621–629. doi:10.1073/pnas.12.11.621. PMID 16577025. Bibcode: 1926PNAS...12..621K.
- ↑ 17.0 17.1 Illingworth, K. K. (1927). "A Repetition of the Michelson–Morley Experiment Using Kennedy's Refinement". Physical Review 30 (5): 692–696. doi:10.1103/PhysRev.30.692. Bibcode: 1927PhRv...30..692I. https://authors.library.caltech.edu/5885/1/ILLpr27.pdf.
- ↑ 18.0 18.1 Joos, G. (1930). "Die Jenaer Wiederholung des Michelsonversuchs". Annalen der Physik 399 (4): 385–407. doi:10.1002/andp.19303990402. Bibcode: 1930AnP...399..385J.
- ↑ 19.0 19.1 19.2 19.3 Miller, Dayton C. (1925). "Ether-Drift Experiments at Mount Wilson". Proceedings of the National Academy of Sciences 11 (6): 306–314. doi:10.1073/pnas.11.6.306. PMID 16587007. Bibcode: 1925PNAS...11..306M.
- ↑ Tomaschek, R. (1924). "Über das Verhalten des Lichtes außerirdischer Lichtquellen". Annalen der Physik 378 (1): 105–126. doi:10.1002/andp.19243780107. Bibcode: 1924AnP...378..105T. http://gallica.bnf.fr/ark:/12148/bpt6k153753/f115.
- ↑ Piccard, A.; Stahel, E. (1926). "L'expérience de Michelson, réalisée en ballon libre". Comptes Rendus 183 (7): 420–421. http://gallica.bnf.fr/ark:/12148/bpt6k3136h/f420.
- ↑ Piccard, A.; Stahel, E. (1927). "Nouveaux résultats obtenus par l'expérience de Michelson". Comptes Rendus 184: 152. http://gallica.bnf.fr/ark:/12148/bpt6k3137t/f152.
- ↑ Piccard, A.; Stahel, E. (1927). "L'absence du vent d'éther au Rigi". Comptes Rendus 184: 1198–1200. http://gallica.bnf.fr/ark:/12148/bpt6k31384/f1198.
- ↑ Michelson, A. A.; Pease, F. G.; Pearson, F. (1929). "Results of repetition of the Michelson–Morley experiment". Journal of the Optical Society of America 18 (3): 181. doi:10.1364/josa.18.000181. Bibcode: 1929JOSA...18..181M.
- ↑ Essen, L. (1955). "A New Æther-Drift Experiment". Nature 175 (4462): 793–794. doi:10.1038/175793a0. Bibcode: 1955Natur.175..793E.
- ↑ Cedarholm, J. P.; Bland, G. F.; Havens, B. L.; Townes, C. H. (1958). "New Experimental Test of Special Relativity". Physical Review Letters 1 (9): 342–343. doi:10.1103/PhysRevLett.1.342. Bibcode: 1958PhRvL...1..342C.
- ↑ Cedarholm, J. P.; Townes, C. H. (1959). "New Experimental Test of Special Relativity". Nature 184 (4696): 1350–1351. doi:10.1038/1841350a0. Bibcode: 1959Natur.184.1350C.
- ↑ Jaseja, T. S.; Javan, A.; Murray, J.; Townes, C. H. (1964). "Test of Special Relativity or of the Isotropy of Space by Use of Infrared Masers". Phys. Rev. 133 (5a): 1221–1225. doi:10.1103/PhysRev.133.A1221. Bibcode: 1964PhRv..133.1221J.
- ↑ Shamir, J.; Fox, R. (1969). "A new experimental test of special relativity". Il Nuovo Cimento B 62 (2): 258–264. doi:10.1007/BF02710136. Bibcode: 1969NCimB..62..258S.
- ↑ Trimmer, William S.; Baierlein, Ralph F.; Faller, James E.; Hill, Henry A. (1973). "Experimental Search for Anisotropy in the Speed of Light". Physical Review D 8 (10): 3321–3326. doi:10.1103/PhysRevD.8.3321. Bibcode: 1973PhRvD...8.3321T.
- ↑ Trimmer, William S.; Baierlein, Ralph F.; Faller, James E.; Hill, Henry A. (1974). "Erratum: Experimental search for anisotropy in the speed of light". Physical Review D 9 (8): 2489. doi:10.1103/PhysRevD.9.2489.2. Bibcode: 1974PhRvD...9R2489T.
- ↑ 32.0 32.1 Müller, H.; Herrmann, S.; Braxmaier, C.; Schiller, S.; Peters, A. (2003). "Modern Michelson–Morley experiment using cryogenic optical resonators". Phys. Rev. Lett. 91 (2): 020401. doi:10.1103/PhysRevLett.91.020401. PMID 12906465. Bibcode: 2003PhRvL..91b0401M.
- ↑ Brillet, A.; Hall, J. L. (1979). "Improved laser test of the isotropy of space". Phys. Rev. Lett. 42 (9): 549–552. doi:10.1103/PhysRevLett.42.549. Bibcode: 1979PhRvL..42..549B.
- ↑ Wolf (2003). "Tests of Lorentz Invariance using a Microwave Resonator". Physical Review Letters 90 (6): 060402. doi:10.1103/PhysRevLett.90.060402. PMID 12633279. Bibcode: 2003PhRvL..90f0402W. https://digital.library.adelaide.edu.au/dspace/bitstream/2440/101285/3/hdl_101285.pdf.
- ↑ Wolf, P.; Tobar, M. E.; Bize, S.; Clairon, A.; Luiten, A. N.; Santarelli, G. (2004). "Whispering Gallery Resonators and Tests of Lorentz Invariance". General Relativity and Gravitation 36 (10): 2351–2372. doi:10.1023/B:GERG.0000046188.87741.51. Bibcode: 2004GReGr..36.2351W.
- ↑ Wolf, P.; Bize, S.; Clairon, A.; Santarelli, G.; Tobar, M. E.; Luiten, A. N. (2004). "Improved test of Lorentz invariance in electrodynamics". Physical Review D 70 (5): 051902. doi:10.1103/PhysRevD.70.051902. Bibcode: 2004PhRvD..70e1902W. https://digital.library.adelaide.edu.au/dspace/bitstream/2440/101283/3/hdl_101283.pdf.
- ↑ Antonini, P.; Okhapkin, M.; Göklü, E.; Schiller, S. (2005). "Test of constancy of speed of light with rotating cryogenic optical resonators". Physical Review A 71 (5): 050101. doi:10.1103/PhysRevA.71.050101. Bibcode: 2005PhRvA..71e0101A.
- ↑ Stanwix, P. L.; Tobar, M. E.; Wolf, P.; Susli, M.; Locke, C. R.; Ivanov, E. N.; Winterflood, J.; Kann, van F. (2005). "Test of Lorentz Invariance in Electrodynamics Using Rotating Cryogenic Sapphire Microwave Oscillators". Physical Review Letters 95 (4): 040404. doi:10.1103/PhysRevLett.95.040404. PMID 16090785. Bibcode: 2005PhRvL..95d0404S.
- ↑ Herrmann, S.; Senger, A.; Kovalchuk, E.; Müller, H.; Peters, A. (2005). "Test of the Isotropy of the Speed of Light Using a Continuously Rotating Optical Resonator". Phys. Rev. Lett. 95 (15): 150401. doi:10.1103/PhysRevLett.95.150401. PMID 16241700. Bibcode: 2005PhRvL..95o0401H.
- ↑ Stanwix, P. L.; Tobar, M. E.; Wolf, P.; Locke, C. R.; Ivanov, E. N. (2006). "Improved test of Lorentz invariance in electrodynamics using rotating cryogenic sapphire oscillators". Physical Review D 74 (8): 081101. doi:10.1103/PhysRevD.74.081101. Bibcode: 2006PhRvD..74h1101S.
- ↑ Müller, H.; Stanwix, Paul L.; Tobar, M. E.; Ivanov, E.; Wolf, P.; Herrmann, S.; Senger, A.; Kovalchuk, E. et al. (2007). "Relativity tests by complementary rotating Michelson–Morley experiments". Phys. Rev. Lett. 99 (5): 050401. doi:10.1103/PhysRevLett.99.050401. PMID 17930733. Bibcode: 2007PhRvL..99e0401M.
- ↑ Nagel, M.; Parker, S.; Kovalchuk, E.; Stanwix, P.; Hartnett, J. V.; Ivanov, E.; Peters, A.; Tobar, M. (2015). "Direct terrestrial test of Lorentz symmetry in electrodynamics to 10−18". Nature Communications 6: 8174. doi:10.1038/ncomms9174. PMID 26323989. Bibcode: 2015NatCo...6.8174N.
Bibliography (Series "A" references)
- ↑ 1.0 1.1 Blum, Edward K.; Lototsky, Sergey V. (2006). Mathematics of physics and engineering. World Scientific. p. 98. ISBN 978-981-256-621-8. https://books.google.com/books?id=nFRG2UizET0C., Chapter 2, p. 98
- ↑ 2.0 2.1 2.2 Staley, Richard (2009), "Albert Michelson, the Velocity of Light, and the Ether Drift", Einstein's generation. The origins of the relativity revolution, Chicago: University of Chicago Press, ISBN 978-0-226-77057-4
- ↑ Albrecht Fölsing (1998). Albert Einstein: A Biography. Penguin Group. ISBN 0-14-023719-4. https://archive.org/details/alberteinsteinbi0000fols.
- ↑ 4.0 4.1 4.2 Robertson, H. P. (1949). "Postulate versus Observation in the Special Theory of Relativity". Reviews of Modern Physics 21 (3): 378–382. doi:10.1103/RevModPhys.21.378. Bibcode: 1949RvMP...21..378R. https://cds.cern.ch/record/1061896/files/RevModPhys.21.378.pdf.
- ↑ 5.0 5.1 5.2 Whittaker, Edmund Taylor (1910). A History of the Theories of Aether and Electricity (1. ed.). Dublin: Longman, Green and Co..
- ↑ 6.0 6.1 6.2 6.3 6.4 Janssen, Michel; Stachel, John (2010). "The Optics and Electrodynamics of Moving Bodies". in Stachel, John. Going Critical. Springer. ISBN 978-1-4020-1308-9. http://www.mpiwg-berlin.mpg.de/Preprints/P265.PDF.
- ↑ Laub, Jakob (1910). "Über die experimentellen Grundlagen des Relativitätsprinzips (On the experimental foundations of the principle of relativity)". Jahrbuch der Radioaktivität und Elektronik 7: 405–463.
- ↑
 Maxwell (1878). "Ether". in Baynes, T.S.. Encyclopædia Britannica. 8 (9th ed.). New York: Charles Scribner's Sons. pp. 568–572.
Maxwell (1878). "Ether". in Baynes, T.S.. Encyclopædia Britannica. 8 (9th ed.). New York: Charles Scribner's Sons. pp. 568–572.
- ↑ Maxwell, James Clerk (1880), "On a Possible Mode of Detecting a Motion of the Solar System through the Luminiferous Ether", Nature 21 (535): 314–5, doi:10.1038/021314c0, Bibcode: 1880Natur..21S.314.
- ↑ 10.0 10.1 Miller, A.I. (1981). Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Reading: Addison–Wesley. p. 24. ISBN 978-0-201-04679-3. https://archive.org/details/alberteinsteinss0000mill/page/24.
- ↑ Fickinger, William (2005). Physics at a Research University: Case Western Reserve, 1830–1990. Cleveland. pp. 18–22, 48. ISBN 978-0977338603. "The Dormitory was located on a now largely unoccupied space between the Biology Building and the Adelbert Gymnasium, both of which still stand on the CWRU campus."
- ↑ Hamerla, Ralph R. (2006). An American Scientist on the Research Frontier: Edward Morley, Community, and Radical Ideas in Nineteenth-Century Science. Springer. pp. 123–152. ISBN 978-1-4020-4089-4. https://books.google.com/books?id=6EcZa6hutfcC&pg=PA123.
- ↑ 13.0 13.1 Miller, Dayton C. (1933). "The Ether-Drift Experiment and the Determination of the Absolute Motion of the Earth". Reviews of Modern Physics 5 (3): 203–242. doi:10.1103/RevModPhys.5.203. Bibcode: 1933RvMP....5..203M.
- ↑ Shankland, R.S. (1964). "Michelson–Morley experiment". American Journal of Physics 31 (1): 16–35. doi:10.1119/1.1970063. Bibcode: 1964AmJPh..32...16S.
- ↑ Feynman, R.P. (1970), "The Michelson–Morley experiment (15-3)", The Feynman Lectures on Physics, 1, Reading: Addison Wesley Longman, ISBN 978-0-201-02115-8, https://feynmanlectures.caltech.edu/I_15.html#Ch15-S3
- ↑ Albert Shadowitz (1988). Special relativity (Reprint of 1968 ed.). Courier Dover Publications. pp. 159–160. ISBN 978-0-486-65743-1. https://archive.org/details/specialrelativit0000shad.
- ↑ Teller, Edward; Teller, Wendy; Talley, Wilson (2002), Conversations on the Dark Secrets of Physics, Basic books, pp. 10–11, ISBN 978-0786752379, https://books.google.com/books?id=QClyAWecl60C&pg=PA10
- ↑ 18.0 18.1 Schumacher, Reinhard A. (1994). "Special Relativity and the Michelson-Morley Interferometer". American Journal of Physics 62 (7): 609–612. doi:10.1119/1.17535. Bibcode: 1994AmJPh..62..609S.
- ↑ Lorentz, Hendrik Antoon (1895), Attempt of a Theory of Electrical and Optical Phenomena in Moving Bodies, Leiden: E.J. Brill, Bibcode: 1895eobk.book.....L
- ↑ 20.0 20.1 Lorentz, Hendrik Antoon (1904), "Electromagnetic phenomena in a system moving with any velocity smaller than that of light", Proceedings of the Royal Netherlands Academy of Arts and Sciences 6: 809–831, Bibcode: 1903KNAB....6..809L
- ↑ Poincaré, Henri (1905), "On the Dynamics of the Electron", Comptes Rendus 140: 1504–1508 (Wikisource translation)
- ↑ Einstein, A (June 30, 1905). "Zur Elektrodynamik bewegter Körper" (in de). Annalen der Physik 17 (10): 890–921. doi:10.1002/andp.19053221004. Bibcode: 1905AnP...322..891E. English translation: Perrett, W. "On the Electrodynamics of Moving Bodies". in Walker, J.. Fourmilab. http://www.fourmilab.ch/etexts/einstein/specrel/www/.
- ↑ Einstein, A. (1916), Relativity: The Special and General Theory, New York: H. Holt and Company
- ↑ 24.0 24.1 Stachel, John (1982), "Einstein and Michelson: the Context of Discovery and Context of Justification", Astronomische Nachrichten 303 (1): 47–53, doi:10.1002/asna.2103030110, Bibcode: 1982AN....303...47S
- ↑ Michael Polanyi, Personal Knowledge: Towards a Post-Critical Philosophy, ISBN:0-226-67288-3, footnote page 10–11: Einstein reports, via Dr N Balzas in response to Polanyi's query, that "The Michelson–Morley experiment had no role in the foundation of the theory." and "..the theory of relativity was not founded to explain its outcome at all."[1]
- ↑ Jeroen, van Dongen (2009), "On the Role of the Michelson–Morley Experiment: Einstein in Chicago", Archive for History of Exact Sciences 63 (6): 655–663, doi:10.1007/s00407-009-0050-5, Bibcode: 2009arXiv0908.1545V
- ↑ 27.0 27.1 Mansouri, R.; Sexl, R.U. (1977). "A test theory of special relativity: III. Second-order tests". Gen. Rel. Gravit. 8 (10): 809–814. doi:10.1007/BF00759585. Bibcode: 1977GReGr...8..809M.
- ↑ Norton, John D. (2004). "Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905". Archive for History of Exact Sciences 59 (1): 45–105. doi:10.1007/s00407-004-0085-6. Bibcode: 2004AHES...59...45N. http://philsci-archive.pitt.edu/archive/00001743/.
- ↑ Swenson, Loyd S. (1970). "The Michelson–Morley–Miller Experiments before and after 1905". Journal for the History of Astronomy 1 (2): 56–78. doi:10.1177/002182867000100108. Bibcode: 1970JHA.....1...56S.
- ↑ Swenson, Loyd S. Jr. (2013). The Ethereal Aether: A History of the Michelson-Morley-Miller Aether-drift Experiments, 1880–1930. University of Texas Press. ISBN 978-0-292-75836-0. https://books.google.com/books?id=kQTUAAAAQBAJ.
- ↑ Thirring, Hans (1926). "Prof. Miller's Ether Drift Experiments". Nature 118 (2959): 81–82. doi:10.1038/118081c0. Bibcode: 1926Natur.118...81T.
- ↑ 32.0 32.1 Michelson, A. A. et al. (1928). "Conference on the Michelson–Morley Experiment Held at Mount Wilson, February, 1927". Astrophysical Journal 68: 341–390. doi:10.1086/143148. Bibcode: 1928ApJ....68..341M.
- ↑ Shankland, Robert S. et al. (1955). "New Analysis of the Interferometer Observations of Dayton C. Miller". Reviews of Modern Physics 27 (2): 167–178. doi:10.1103/RevModPhys.27.167. Bibcode: 1955RvMP...27..167S.
- ↑ Roberts, T.J. (2006). "An Explanation of Dayton Miller's Anomalous "Ether Drift" Result". arXiv:physics/0608238.
- ↑ Relativity FAQ (2007): What is the experimental basis of Special Relativity?
- ↑ Haugan, Mark P.; Will, Clifford M. (May 1987). "Modern tests of special relativity". Physics Today 40 (5): 67–76. doi:10.1063/1.881074. Bibcode: 1987PhT....40e..69H. http://docuserv.ligo.caltech.edu/docs/public/P/P870007-00.pdf. Retrieved 14 July 2012.
External links
- Roberts, T; Schleif, S (2007). "What is the experimental basis of Special Relativity?". in Dlugosz, JM. Usenet Physics FAQ. University of California, Riverside. http://math.ucr.edu/home/baez/physics/Relativity/SR/experiments.html.
- "Episode 41: The Michelson Morley Experiment - The Mechanical Universe". caltech. December 19, 2016. https://www.youtube.com/watch?v=Ip_jdcA8fcw.
 |