Physics:Forouhi–Bloomer model

From HandWiki
Short description: Popular optical dispersion relation
Forouhi-Bloomer model. The real (blue solid line) and imaginary (orange dashed line) components of complex refractive index are plotted for model with parameters [math]\displaystyle{ E_{g} = }[/math] 1.3 eV, [math]\displaystyle{ A = }[/math] 1.4910 eV, [math]\displaystyle{ B = }[/math] 5.2139 eV, [math]\displaystyle{ C = }[/math] 8.6170 eV[math]\displaystyle{ ^{2} }[/math], and [math]\displaystyle{ n_{\infty} = }[/math] 1.5256. These parameters approximate amorphous silicon.[1]

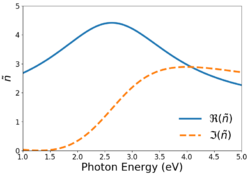
The Forouhi–Bloomer model is a mathematical formula for the frequency dependence of the complex-valued refractive index. The model can be used to fit the refractive index of amorphous and crystalline semiconductor and dielectric materials at energies near and greater than their optical band gap.[2][3][4][5][6] The dispersion relation bears the names of Rahim Forouhi and Iris Bloomer, who created the model and interpreted the physical significance of its parameters.[1][7] The model is aphysical due to its incorrect asymptotic behavior and non-Hermitian character. These shortcomings inspired modified versions of the model[8][9][10] as well as development of the Tauc–Lorentz model.

Mathematical formulation

The complex refractive index is given by

[math]\displaystyle{ \tilde{n}(E) = n(E) + i \kappa(E) }[/math]

where

  • [math]\displaystyle{ n }[/math] is the real component of the complex refractive index, commonly called the refractive index,
  • [math]\displaystyle{ \kappa }[/math] is the imaginary component of the complex refractive index, commonly called the extinction coefficient,
  • [math]\displaystyle{ E }[/math] is the photon energy (related to the angular frequency by [math]\displaystyle{ E=\hbar\omega }[/math]).

The real and imaginary components of the refractive index are related to one another through the Kramers-Kronig relations. Forouhi and Bloomer derived a formula for [math]\displaystyle{ \kappa(E) }[/math] for amorphous materials. The formula and complementary Kramers–Kronig integral are given by[1]

[math]\displaystyle{ \kappa(E) = \frac{A \left( E - E_{g} \right)^{2}}{E^{2} - B E + C} }[/math]
[math]\displaystyle{ n(E) = n_{\infty} + \frac{1}{\pi} \mathcal{P} \int_{-\infty}^{\infty} \frac{\kappa(\xi) - \kappa_{\infty}}{\xi - E} d\xi }[/math]

where

  • [math]\displaystyle{ E_{g} }[/math] is the bandgap of the material,
  • [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], [math]\displaystyle{ C }[/math], and [math]\displaystyle{ n_{\infty} }[/math] are fitting parameters,
  • [math]\displaystyle{ \mathcal{P} }[/math] denotes the Cauchy principal value,
  • [math]\displaystyle{ \kappa_{\infty} = \lim_{E \rightarrow \infty} \kappa(E) = A }[/math].

[math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ C }[/math] are subject to the constraints [math]\displaystyle{ A\gt 0 }[/math], [math]\displaystyle{ B\gt 0 }[/math], [math]\displaystyle{ C\gt 0 }[/math], and [math]\displaystyle{ 4C - B^{2} \gt 0 }[/math]. Evaluating the Kramers-Kronig integral,

[math]\displaystyle{ n(E) = n_{\infty} + \frac{B_{0} E + C_{0}}{E^{2} - B E + C} }[/math]

where

  • [math]\displaystyle{ Q = \frac{1}{2} \sqrt{4 C - B^{2}} }[/math],
  • [math]\displaystyle{ B_{0} = \frac{A}{Q} \left( - \frac{1}{2} B^{2} + E_{g} B - E_{g}^{2} + C \right) }[/math],
  • [math]\displaystyle{ C_{0} = \frac{A}{Q} \left( \frac{1}{2} B \left( E_{g}^{2} + C \right) - 2 E_{g} C \right) }[/math].

The Forouhi–Bloomer model for crystalline materials is similar to that of amorphous materials. The formulas for [math]\displaystyle{ n(E) }[/math] and [math]\displaystyle{ \kappa(E) }[/math] are given by[7]

[math]\displaystyle{ n(E) = n_{\infty} + \sum_{j} \frac{B_{0,j} E + C_{0,j}}{E^{2} - B_{j} E + C_{j}} }[/math].
[math]\displaystyle{ \kappa(E) = \left( E - E_{g} \right)^{2} \sum_{j} \frac{A_{j}}{E^{2} - B_{j} E + C_{j}} }[/math].

where all variables are defined similarly to the amorphous case, but with unique values for each value of the summation index [math]\displaystyle{ j }[/math]. Thus, the model for amorphous materials is a special case of the model for crystalline materials when the sum is over a single term only.

References

  1. ↑ 1.0 1.1 1.2 Forouhi, A. Rahim; Bloomer, Iris (1986). "Optical dispersion relations for amorphous semiconductors and amorphous dielectrics". Physical Review B 34 (10): 7018–7026. doi:10.1103/PhysRevB.34.7018. PMID 9939354. Bibcode: 1986PhRvB..34.7018F. https://doi.org/10.1103/PhysRevB.34.7018. Retrieved 2021-11-07. 
  2. ↑ Chrysicopoulou, P.; Davazoglou, D.; Trapalis, Chr; Kordas, G. (1998). "Optical properties of very thin (<100 nm) sol–gel TiO2 films". Thin Solid Films 323 (1–2): 188–193. doi:10.1016/S0040-6090(97)01018-3. Bibcode: 1998TSF...323..188C. https://doi.org/10.1016/S0040-6090(97)01018-3. Retrieved 2021-11-16. 
  3. ↑ Liu, Y. C.; Hsieh, J. H.; Tung, S. K. (2006). "Extraction of optical constants of zinc oxide thin films by ellipsometry with various models". Thin Solid Films 510 (1–2): 32–38. doi:10.1016/j.tsf.2005.10.089. Bibcode: 2006TSF...510...32L. https://doi.org/10.1016/j.tsf.2005.10.089. Retrieved 2021-11-16. 
  4. ↑ Laidani, N.; Bartali, R.; Gottardi, G.; Anderle, M.; Cheyssac, P. (2007). "Optical absorption parameters of amorphous carbon films from Forouhi–Bloomer and Tauc–Lorentz models: a comparative study". Journal of Physics: Condensed Matter 20 (1): 015216. doi:10.1088/0953-8984/20/01/015216. https://doi.org/10.1088/0953-8984/20/01/015216. Retrieved 2021-11-16. 
  5. ↑ Torkaman, N. M.; Ganjkhanlou, Y.; Kazemzad, M.; Dabaghi, H. H.; Keyanpour-Rad, M. (2010). "Crystallographic parameters and electro-optical constants in ITO thin films". Materials Characterization 61 (3): 362–370. doi:10.1016/j.matchar.2009.12.020. https://doi.org/10.1016/j.matchar.2009.12.020. Retrieved 2021-11-16. 
  6. ↑ Löper, Philipp; Stuckelberger, Michael; Niesen, Bjoern; Werner, Jérémie; Filipič, Miha; Moon, Soo-Jin; Yum, Jun-Ho; Topič, Marko et al. (2015). "Complex Refractive Index Spectra of CH3NH3PbI3 Perovskite Thin Films Determined by Spectroscopic Ellipsometry and Spectrophotometry". The Journal of Physical Chemistry Letters 6 (1): 66–71. doi:10.1021/jz502471h. PMID 26263093. https://doi.org/10.1021/jz502471h. Retrieved 2021-11-16. 
  7. ↑ 7.0 7.1 Forouhi, A. Rahim; Bloomer, Iris (1988). "Optical properties of crystalline semiconductors and dielectrics". Physical Review B 38 (3): 1865–1874. doi:10.1103/PhysRevB.38.1865. PMID 9946471. Bibcode: 1988PhRvB..38.1865F. https://doi.org/10.1103/PhysRevB.38.1865. Retrieved 2021-11-07. 
  8. ↑ McGahan, William A.; Makovicka, Tim; Hale, Jeffrey; Woollam, John A. (1994). "Modified Forouhi and Bloomer dispersion model for the optical constants of amorphous hydrogenated carbon thin films". Thin Solid Films 253 (1): 57–61. doi:10.1016/0040-6090(94)90294-1. Bibcode: 1994TSF...253...57M. https://doi.org/10.1016/0040-6090(94)90294-1. Retrieved 2021-11-07. 
  9. ↑ Liu, Yong; Xu, Gang; Song, Chenlu; Weng, Wenjian; Du, Piyi; Han, Gaorong (2007). "Modification on Forouhi and Bloomer model for the optical properties of amorphous silicon thin films". Thin Solid Films 515 (7): 3910–3913. doi:10.1016/j.tsf.2006.11.003. Bibcode: 2007TSF...515.3910L. https://doi.org/10.1016/j.tsf.2006.11.003. Retrieved 2021-11-16. 
  10. ↑ Forouhi, A. Rahim; Bloomer, Iris (2019). "New dispersion equations for insulators and semiconductors valid throughout radio-waves to extreme ultraviolet spectral range". Journal of Physics Communications 3 (3): 035022. doi:10.1088/2399-6528/ab0603. Bibcode: 2019JPhCo...3c5022F. 

See also



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Forouhi–Bloomer_model&oldid=3277477"