Physics:Brendel–Bormann oscillator model
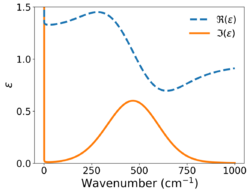
The Brendel–Bormann oscillator model is a mathematical formula for the frequency dependence of the complex-valued relative permittivity, sometimes referred to as the dielectric function. The model has been used to fit to the complex refractive index of materials with absorption lineshapes exhibiting non-Lorentzian broadening, such as metals[1] and amorphous insulators,[2][3][4][5] across broad spectral ranges, typically near-ultraviolet, visible, and infrared frequencies. The dispersion relation bears the names of R. Brendel and D. Bormann, who derived the model in 1992,[2] despite first being applied to optical constants in the literature by Andrei M. Efimov and E. G. Makarova in 1983.[6][7][8] Around that time, several other researchers also independently discovered the model.[3][4][5] The Brendel-Bormann oscillator model is aphysical because it does not satisfy the Kramers–Kronig relations. The model is non-causal, due to a singularity at zero frequency, and non-Hermitian. These drawbacks inspired J. Orosco and C. F. M. Coimbra to develop a similar, causal oscillator model.[9][10]
Mathematical formulation
The general form of an oscillator model is given by[2]
- [math]\displaystyle{ \varepsilon(\omega) = \varepsilon_{\infty} + \sum_{j} \chi_{j} }[/math]
where
- [math]\displaystyle{ \varepsilon }[/math] is the relative permittivity,
- [math]\displaystyle{ \varepsilon_{\infty} }[/math] is the value of the relative permittivity at infinite frequency,
- [math]\displaystyle{ \omega }[/math] is the angular frequency,
- [math]\displaystyle{ \chi_{j} }[/math] is the contribution from the [math]\displaystyle{ j }[/math]th absorption mechanism oscillator.
The Brendel-Bormann oscillator is related to the Lorentzian oscillator [math]\displaystyle{ \left(\chi^{L}\right) }[/math] and Gaussian oscillator [math]\displaystyle{ \left(\chi^{G}\right) }[/math], given by
- [math]\displaystyle{ \chi_{j}^{L}(\omega; \omega_{0,j}) = \frac{s_{j}}{\omega_{0,j}^{2} - \omega^{2} - i \Gamma_{j} \omega} }[/math]
- [math]\displaystyle{ \chi_{j}^{G}(\omega) = \frac{1}{\sqrt{2 \pi} \sigma_{j}} \exp{\left[ -\left( \frac{\omega}{\sqrt{2} \sigma_{j}} \right)^{2} \right]} }[/math]
where
- [math]\displaystyle{ s_{j} }[/math] is the Lorentzian strength of the [math]\displaystyle{ j }[/math]th oscillator,
- [math]\displaystyle{ \omega_{0,j} }[/math] is the Lorentzian resonant frequency of the [math]\displaystyle{ j }[/math]th oscillator,
- [math]\displaystyle{ \Gamma_{j} }[/math] is the Lorentzian broadening of the [math]\displaystyle{ j }[/math]th oscillator,
- [math]\displaystyle{ \sigma_{j} }[/math] is the Gaussian broadening of the [math]\displaystyle{ j }[/math]th oscillator.
The Brendel-Bormann oscillator [math]\displaystyle{ \left(\chi^{BB}\right) }[/math] is obtained from the convolution of the two aforementioned oscillators in the manner of
- [math]\displaystyle{ \chi_{j}^{BB}(\omega) = \int_{-\infty}^{\infty} \chi_{j}^{G}(x-\omega_{0,j}) \chi_{j}^{L}(\omega; x) dx }[/math],
which yields
- [math]\displaystyle{ \chi_{j}^{BB}(\omega) = \frac{i \sqrt{\pi} s_{j}}{2 \sqrt{2} \sigma_{j} a_{j}(\omega)} \left[ w\left( \frac{a_{j}(\omega) - \omega_{0,j}}{\sqrt{2}\sigma_{j}} \right) + w\left( \frac{a_{j}(\omega) + \omega_{0,j}}{\sqrt{2}\sigma_{j}} \right) \right] }[/math]
where
- [math]\displaystyle{ w(z) }[/math] is the Faddeeva function,
- [math]\displaystyle{ a_{j} = \sqrt{\omega^{2}+i \Gamma_{j} \omega} }[/math].
The square root in the definition of [math]\displaystyle{ a_{j} }[/math] must be taken such that its imaginary component is positive. This is achieved by:
- [math]\displaystyle{ \Re\left( a_{j} \right) = \omega \sqrt{\frac{\sqrt{1+\left( \Gamma_{j}/\omega \right)^{2}}+1}{2}} }[/math]
- [math]\displaystyle{ \Im\left( a_{j} \right) = \omega \sqrt{\frac{\sqrt{1+\left( \Gamma_{j}/\omega \right)^{2}}-1}{2}} }[/math]
References
- ↑ Rakić, Aleksandar D.; Djurišić, Aleksandra B.; Elazar, Jovan M.; Majewski, Marian L. (1998). "Optical properties of metallic films for vertical-cavity optoelectronic devices". Applied Optics 37 (22): 5271–5283. doi:10.1364/AO.37.005271. PMID 18286006. Bibcode: 1998ApOpt..37.5271R. https://doi.org/10.1364/AO.37.005271. Retrieved 2021-10-13.
- ↑ 2.0 2.1 2.2 Brendel, R.; Bormann, D. (1992). "An infrared dielectric function model for amorphous solids". Journal of Applied Physics 71 (1): 1–6. doi:10.1063/1.350737. Bibcode: 1992JAP....71....1B. https://doi.org/10.1063/1.350737. Retrieved 2021-10-13.
- ↑ 3.0 3.1 Naiman, M. L.; Kirk, C. T.; Aucoin, R. J.; Terry, F. L.; Wyatt, P. W.; Senturia, S. D. (1984). "Effect of Nitridation of Silicon Dioxide on Its Infrared Spectrum". Journal of the Electrochemical Society 131 (3): 637–640. doi:10.1149/1.2115648. Bibcode: 1984JElS..131..637N. https://doi.org/10.1149/1.2115648. Retrieved 2021-10-20.
- ↑ 4.0 4.1 Kučírková, A.; Navrátil, K. (1994). "Interpretation of Infrared Transmittance Spectra of SiO2 Thin Films". Applied Spectroscopy 48 (1): 113–120. doi:10.1366/0003702944027534. Bibcode: 1994ApSpe..48..113K. http://www.osapublishing.org/as/abstract.cfm?URI=as-48-1-113. Retrieved 2021-10-20.
- ↑ 5.0 5.1 Hobert, H.; Dunken, H. H. (1996). "Modelling of dielectric functions of glasses by convolution". Journal of Non-Crystalline Solids 195 (1–2): 64–71. doi:10.1016/0022-3093(95)00517-X. Bibcode: 1996JNCS..195...64H. https://doi.org/10.1016/0022-3093(95)00517-X. Retrieved 2021-10-20.
- ↑ Efimov, Andrei M.; Makarova, E. G. (1983). "[Vitreous state and the dispersion theory]" (in ru). pp. 165–71.
- ↑ Efimov, Andrei M.; Makarova, E. G. (1985). "[Dispersion equation for the complex equation constant of vitreous solids and dispersion analysis of their reflection spectra]" (in ru). Fiz. Khim. Stekla 11 (4): 385–401.
- ↑ Efimov, A. M. (1996). "Quantitative IR spectroscopy: Applications to studying glass structure and properties". Journal of Non-Crystalline Solids 203: 1–11. doi:10.1016/0022-3093(96)00327-4. Bibcode: 1996JNCS..203....1E. https://doi.org/10.1016/0022-3093(96)00327-4. Retrieved 2021-10-13.
- ↑ Orosco, J.; Coimbra, C. F. M. (2018). "On a causal dispersion model for the optical properties of metals". Applied Optics 57 (19): 5333–5347. doi:10.1364/AO.57.005333. PMID 30117825. Bibcode: 2018ApOpt..57.5333O. https://doi.org/10.1364/AO.57.005333. Retrieved 2021-10-14.
- ↑ Orosco, J.; Coimbra, C. F. M. (2018). "Optical response of thin amorphous films to infrared radiation". Physical Review B 97 (9): 094301. doi:10.1103/PhysRevB.97.094301. Bibcode: 2018PhRvB..97i4301O. https://doi.org/10.1103/PhysRevB.97.094301. Retrieved 2021-10-14.
See also
- Cauchy equation
- Sellmeier equation
- Forouhi–Bloomer model
- Tauc–Lorentz model
- Lorentz oscillator model
 |

