Physics:Harmonic spectrum

Approximating a square wave by $\sin (t)+\sin (3t)/3+\sin (5t)/5$

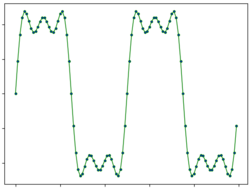
A harmonic spectrum is a spectrum containing only frequency components whose frequencies are whole number multiples of the fundamental frequency; such frequencies are known as harmonics. "The individual partials are not heard separately but are blended together by the ear into a single tone."

In other words, if $\omega$ is the fundamental frequency, then a harmonic spectrum has the form

$\{\dots ,-2\omega ,-\omega ,0,\omega ,2\omega ,\dots \}.$

A standard result of Fourier analysis is that a function has a harmonic spectrum if and only if it is periodic.

See also

• Fourier series
• Harmonic series (music)
• Periodic function
• Scale of harmonics
• Undertone series