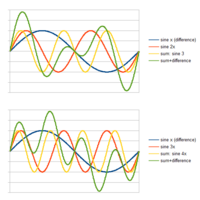
Physics:Combination tone

Combination tones: Unison, just perfect fifth, and octave are played in top row while A220 is sustained in second row, producing third row sum tones and fourth row difference tones. Frequencies are marked in Hz. Midi example contains all four voices for illustration only. Play 

Difference tones (bottom) between "Yankee Doodle" in F (top) and a drone on C (middle) Play top , drone , both , difference tones , or all three 

Sum and difference of frequencies (left) and sum and difference of two pairs of sine waves (right) with frequencies of 1 and 2 (top) and 1 and 3 (bottom)

sum and difference of the frequencies

sum and difference of the sine waves

A combination tone (also called resultant or subjective tone) is a psychoacoustic phenomenon of an additional tone or tones that are artificially perceived when two real tones are sounded at the same time. Their discovery is credited to the violinist Giuseppe Tartini (although he was not the first, see Georg Andreas Sorge) and so they are also called Tartini tones.

There are two types of combination tones: sum tones whose frequencies are found by adding the frequencies of the real tones, and difference tones whose frequencies are the difference between the frequencies of the real tones. "Combination tones are heard when two pure tones (i.e., tones produced by simple harmonic sound waves having no overtones), differing in frequency by about 50 cycles per second [Hertz] or more, sound together at sufficient intensity."

Combination tones can also be produced electronically by combining two signals in a circuit that has nonlinear distortion, such as an amplifier subject to clipping or a ring modulator.

Explanation

One way a difference tone can be heard is when two tones with fairly complete sets of harmonics make a just fifth. This can be explained as an example of the missing fundamental phenomenon. If [math]\displaystyle{ f }[/math] is the missing fundamental frequency, then [math]\displaystyle{ 2f }[/math] would be the frequency of the lower tone, and its harmonics would be [math]\displaystyle{ 4f, 6f, 8f, }[/math] etc. Since a fifth corresponds to a frequency ratio of 2:3, the higher tone and its harmonics would then be [math]\displaystyle{ 3f, 6f, 9f, }[/math] etc. When both tones are sounded, there are components with frequencies of [math]\displaystyle{ 2f, 3f, 4f, 6f, 8f, 9f, }[/math] etc. The missing fundamental is heard because so many of these components refer to it.

The specific phenomenon that Tartini discovered was physical. Sum and difference tones are thought to be caused sometimes by the non-linearity of the inner ear. This causes intermodulation distortion of the various frequencies which enter the ear. They are combined linearly, generating relatively faint components with frequencies equal to the sums and differences of whole multiples of the original frequencies. Any components which are heard are usually lower, with the most commonly heard frequency being just the difference tone, [math]\displaystyle{ f_2-f_1 }[/math], though this may be a consequence of the other phenomena. Although much less common, the following frequencies may also be heard:

[math]\displaystyle{ 2f_1 - f_2, 3f_1 - 2f_2, \ldots, f_1 - k(f_2 - f_1) }[/math]

For a time it was thought that the inner ear was solely responsible whenever a sum or difference tone was heard. However, experiments show evidence that even when using headphones providing a single pure tone to each ear separately, listeners may still hear a difference tone. Since the peculiar non-linear physics of the ear doesn't come into play in this case, it is thought that this must be a separate, neural phenomenon. Compare binaural beats.

Heinz Bohlen proposed what is now known as the Bohlen–Pierce scale on the basis of combination tones, as well as the 833 cents scale.

Resultant tone

A resultant tone is "produced when any two loud and sustained musical sounds are heard at the same time."

In pipe organs, this is done by having two pipes, one pipe of the note being played, and another harmonically related, typically at its fifth, being sounded at the same time. The result is a pitch at a common subharmonic of the pitches played (one octave below the first pitch when the second is the fifth, 3:2, two octaves below when the second is the major third, 5:4). This effect is useful especially in the lowest ranks of the pipe organ where cost or space could prohibit having a rank of such low pitch. For example, a 32' pipe would be costly and take up as much as 16' of vertical space (if capped) or more commonly 17-32' (if open-ended) for each pipe. Using a resultant tone for such low pitches reduces the cost and space factor, but does not sound as full as a true 32' pipe. The effect can be enhanced by using further ranks in the harmonic series of the desired resultant tone.

This effect is most often used in the lowest octave of the organ only. It can vary from highly effective to disappointing depending on several factors, primarily the skill of the organ voicer, and the acoustics of the room the instrument is installed in.

It is possible to produce a melody with resultant tones from multiple harmonics played by two or more instruments. There is an example with seven saxophones.

See also

• Power chord#Analysis
• Ring modulation
• Beat (acoustics)

Further reading

• Adrianus J. M. Houtsma, Julius L. Goldstein, "Percepetion of Musical Intervals: Evidence for the Central Origin of the Pitch of Complex Tones", Massachusetts Institute of Technology, Research Laboratory of Electronics, Technical Report 484, October 1, 1971.
• Adrian Wehlte, Trios for Two, Practice book with combination tones for two flutes or two recorders – Explanation and examples, Edition Floeno 2020, ISMN 979-0-9000114-2-8

External links

• Titchener Difference Tones Training
• Difference tones on the harmonica
• Pitch Perception Lecture Notes
• Tartini computer program. Uses combination tones for pitch recognition. If certain intervals are played in double-stop, the program can display its Tartini-tone.
• http://www.organstops.org/r/Resultant.html