Physics:Horseshoe vortex

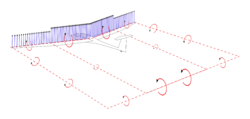

The horseshoe vortex model is a simplified representation of the vortex system present in the flow of air around a wing. This vortex system is modelled by the bound vortex (bound to the wing) and two trailing vortices, therefore having a shape vaguely reminiscent of a horseshoe.[1][2] A starting vortex is shed as the wing begins to move through the fluid. This vortex dissipates under the action of viscosity,[3] as do the trailing vortices which eventually dissipate far behind the aircraft.
The downwash is associated with induced drag and is a component of the system of trailing vortices.[4]
The horseshoe vortex model is unrealistic in that it implies uniform circulation (and hence, according to the Kutta–Joukowski theorem, uniform lift) at all sections on the wingspan. In a more realistic model, the lifting-line theory, the vortex strength varies along the wingspan, and the loss in vortex strength is shed as a vortex sheet all along the trailing edge, rather than as a single trail at the wing-tips.[5] Nevertheless, the simpler horseshoe vortex model used with a reduced effective wingspan but same mid-plane circulation provides an adequate model for the flows induced far from the aircraft.
The term horseshoe vortex is also used in wind engineering to describe the flow pattern created by strong winds around the base of a tall building. This effect is amplified by the presence of a low-rise building just upwind. This effect was studied at the UK Building Research Establishment between 1963 and 1973[6] and the cause of the effect is described in contemporary wind engineering text books.[7]
In hydrodynamics, a form of horseshoe vortex forms around bluff bodies in the flowing water, for instance around bridge piers.[8] They can cause scouring of bed materials from both upstream and downstream of the pier. In nature, a horseshoe vortex can cause a horseshoe cloud to form.[9]
Notes
- ↑ Millikan, Clark B., Aerodynamics of the Airplane, Figure 1.35
- ↑ McCormick, Barnes W., Aerodynamics, Aeronautics, and Flight Mechanics, Chapter 3
- ↑ "Shed Vortex". NASA Glenn Research Center. https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/shed-vorticity/.
- ↑ McCormick, Barnes W., Aerodynamics, Aeronautics, and Flight Mechanics, Chapter 4
- ↑ McCormick, Barnes W., Aerodynamics, Aeronautics, and Flight Mechanics, Figure 4.21
- ↑ Penwarden, AD. Wise, AFE. Wind environment around buildings, cover illustration
- ↑ Cook, NJ. The designer's guide to wind loading of building structures, Part 1, Figure 8.7
- ↑ Dargahi, Bijan (1989). "The turbulent flow field around a circular cylinder". Experiments in Fluids 8 (1–2): 1–12. doi:10.1007/BF00203058. Bibcode: 1989ExFl....8....1D.
- ↑ "An incredibly rare 'horseshoe cloud' was spotted in Nevada and it kept the meme-makers busy". 12 March 2018. https://www.independent.ie/world-news/and-finally/an-incredibly-rare-horseshoe-cloud-was-spotted-in-nevada-and-it-kept-the-mememakers-busy-36691086.html.
References
- Anderson, John D. (2007), Fundamentals of Aerodynamics, Section 5.3 (4th ed.), McGraw-Hill, New York NY. ISBN 978-0-07-295046-5
- L. J. Clancy (1975), Aerodynamics, Section 8.10, Pitman Publishing Limited, London ISBN 0-273-01120-0
- Cook, N.J. (1985), The designer's guide to wind loading of building structures, Part 1, Butterworths, London ISBN 0-408-00870-9
- McCormick, Barnes W., (1979), Aerodynamics, Aeronautics, and Flight Mechanics, John Wiley & Sons, Inc. New York ISBN 0-471-03032-5
- Millikan, Clark B., (1941), Aerodynamics of the Airplane, Section 1-6 John Wiley and Sons, Inc., New York
- Penwarden, A.D., Wise, A.F.E., (1975) Wind environment around buildings, HMSO, London ISBN 0-11-670533-7.
- Piercy, N.A.V. (1944), Elementary Aerodynamics, Article 213, The English Universities Press Ltd., London.
- Von Mises, Richard, (1959), Theory of Flight, Chapter IX - section 4, Dover Publications, Inc., New York ISBN 0-486-60541-8
See also
- Helmholtz's theorems
- Kutta condition
- Kutta–Joukowski theorem
- Prandtl's lifting-line model
- Trailing vortices
 |
