Physics:Circulation (fluid dynamics)

Field lines of a vector field v, around the boundary of an open curved surface with infinitesimal line element dl along boundary, and through its interior with dS the infinitesimal surface element and n the unit normal to the surface. Top: Circulation is the line integral of v around a closed loop C. Project v along dl, then sum. Here v is split into components perpendicular (⊥) parallel ( ‖ ) to dl, the parallel components are tangential to the closed loop and contribute to circulation, the perpendicular components do not. Bottom: Circulation is also the flux of vorticity ω through the surface, and the curl of v is heuristically depicted as a helical arrow (not a literal representation). Note the projection of v along dl and curl of v may be in the negative sense, reducing the circulation.

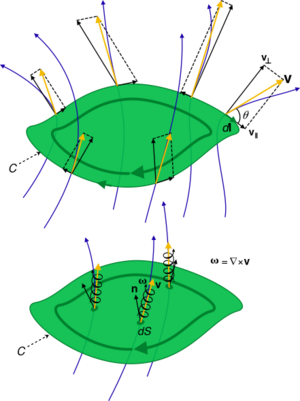
In fluid dynamics, circulation is the line integral of the velocity field, around a closed curve.

Notation

Circulation is normally denoted Γ (Greek uppercase gamma).

History

Circulation was first used independently by Frederick Lanchester, Martin Kutta and Nikolai Zhukovsky.

Definition

If V is the fluid velocity on a small element of a defined curve, and dl is a vector representing the differential length of that small element, the contribution of that differential length to circulation is dΓ:

[math]\displaystyle{ d\Gamma=\mathbf{V}\cdot \mathbf{dl}=|\mathbf{V}||d\mathbf{l}|\cos \theta }[/math]

where θ is the angle between the vectors V and dl.

The circulation Γ around a closed curve C is the line integral:

[math]\displaystyle{ \Gamma=\oint_{C}\mathbf{V}\cdot d\mathbf{l} }[/math]

The dimensions of circulation are length squared, divided by time; L²⋅T⁻¹, which is equivalent to velocity times length.

In potential flow with a region of vorticity, all closed curves that enclose the vorticity have the same numerical value for circulation. The circulation around a region of vorticity is the same for all closed curves that enclose the vorticity.

Kutta–Joukowski theorem

The lift per unit span (L') acting on a body in a two-dimensional inviscid flow field can be expressed as the product of the circulation Γ about the body, the fluid density ρ, and the speed of the body relative to the free-stream V. Thus,

[math]\displaystyle{ L' = \rho V \Gamma\! }[/math]

This is known as the Kutta–Joukowski theorem.

This equation applies around airfoils, where the circulation is generated by airfoil action; and around spinning objects experiencing the Magnus effect where the circulation is induced mechanically. In airfoil action, the magnitude of the circulation is determined by the Kutta condition.

The circulation on every closed curve around the airfoil has the same value, and is related to the lift generated by each unit length of span. Provided the closed curve encloses the airfoil, the choice of curve is arbitrary.

Circulation is often used in computational fluid dynamics as an intermediate variable to calculate forces on an airfoil or other body.

Relation to vorticity

Circulation can be related to vorticity:

[math]\displaystyle{ \mathbf{\omega} = \nabla\times\mathbf{V} }[/math]

by Stokes' theorem:

[math]\displaystyle{ \Gamma=\oint_{\partial S}\mathbf{V}\cdot d\mathbf{l}=\int\!\!\!\int_S \mathbf{\omega} \cdot d\mathbf{S} }[/math]

where the closed integration path (indicated by "∂S") is the boundary or perimeter of a surface S whose local perpendicular unit vector is dS. Thus vorticity is the circulation per unit area, taken around a local infinitesimal loop. Correspondingly, the flux of vorticity vectors through a surface S is equal to the circulation around its perimeter.

See also

• Biot–Savart law
• Kutta condition
• Kutta–Joukowski theorem
• Kelvin's circulation theorem