Physics:Laser beam quality

Laser beams

In laser science, laser beam quality defines aspects of the beam illumination pattern and the merits of a particular laser beam's propagation and transformation properties (space-bandwidth criterion). By observing and recording the beam pattern, for example, one can infer the spatial mode properties of the beam and whether or not the beam is being clipped by an obstruction; By focusing the laser beam with a lens and measuring the minimum spot size, the number of times diffraction limit or focusing quality can be computed.

Anthony E. Siegman was the first to propose the formalism for a laser beam quality factor that could be measured and used to compare different beams, independent of wavelength. The factor is called beam propagation ratio (M²), and it is closely related to the beam parameter product. While the M² factor does not give detail on the spatial characteristics of the beam, it does indicate how close it is to being a fundamental-mode Gaussian beam. It also determines the smallest spot size for the beam, as well as the beam divergence. M² can also give an indication of beam distortions due to, for example, power-induced thermal lensing in the laser gain medium, since it will increase.

There are some limitations to the M² parameter as a simple quality metric. It can be difficult to measure accurately, and factors such as background noise can create large errors in M². Beams with power well out in the "tails" of the distribution have M² much larger than one would expect. In theory, an idealized tophat laser beam has infinite M², although this is not true of any physically realizable tophat beam. For a pure Bessel beam, one cannot even compute M².

The definition of "quality" also depends on the application. While a high-quality single-mode Gaussian beam (M² close to unity) is optimum for many applications, for other applications a uniform multimode tophat beam intensity distribution is required. An example is laser surgery.

Power-in-the-bucket and Strehl ratio are two other attempts to define beam quality. Both these methods use a laser beam profiler to measure how much power is delivered to a given area. There is also no simple conversion between M², power-in-the-bucket, and Strehl ratio.

M² definitions

M² definition

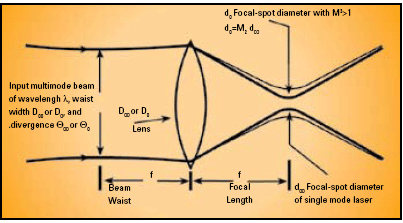
The equation for the divergence of a pure Gaussian TEM₀₀ unfocused beam propagating through space is given by

[math]\displaystyle{ \Theta_{00}={4\lambda \over \pi D_{00}} }[/math], (1)

where D₀₀ is the diameter of the beam waist, and λ is the wavelength. Higher mode beams often start with a larger beam waist, D₀, and/or have a faster divergence Θ₀. In this case Equation (1) becomes

[math]\displaystyle{ \Theta_0=M^2 {4\lambda \over \pi D_0} }[/math], (2)

where Θ₀ and D₀ are the divergence and waist of a higher mode beam and M² is greater than 1 and is named the "Beam Propagation Ratio" per the ISO 11146 standard. When a Gaussian laser beam is focused, the focused spot diameter is defined by

[math]\displaystyle{ d_{00}={4\lambda f \over \pi D_{00}} }[/math], (3)

where d₀₀ is the ideal focused spot diameter, f is the focal length of the focusing lens, and D₀₀ is the input beam waist and is placed one focal length from the lens as shown in the figure. However, when a multimode beam is focused, Equation (3) becomes

[math]\displaystyle{ d_0=M^2 {4\lambda f \over \pi D_0} }[/math]. (4)

M² measurement

M² cannot be determined from a single beam profile measurement. The ISO/DIS 11146 define that M² should be calculated from a series of measurements as shown in the figure below. M² is measured on real beams by focusing the beam with a fixed position lens of known focal length, and then measuring the characteristics of the beam waist and divergence. These measurements can be taken with a laser beam profiler.

Measurement positions for obtaining M²

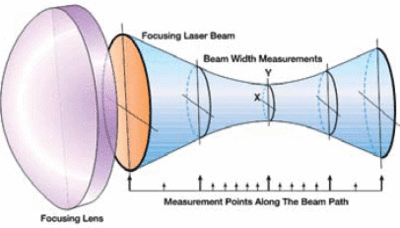
The multiple measurements ensure that the minimum beam diameter is found and enable a "curve fit" that improves the accuracy of the calculation by minimizing measurement error.